一道题的反思
2016-04-05魏计玲
魏计玲
(山西省晋中市榆次五中)
探索篇·方法展示
一道题的反思
魏计玲
(山西省晋中市榆次五中)
今天,学生拿着题来问我,题目是这样的:如图1,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,△ECF的周长为4,则正方形ABCD的边长为______
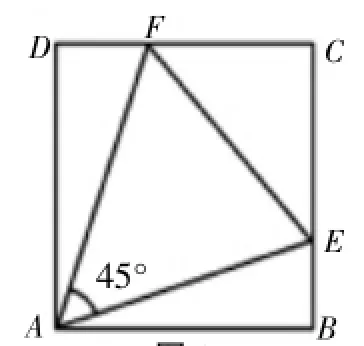
图1
很熟悉的图形,前两天刚解决过的一道题,当时是求证EF= BE+FD,这两道题如出一辙,可学生为什么把它们联系不起来呢?仔细想来,学生大量的做题,每道题独立出现,如果不深入思考,今天做会这个,明天稍有变化,又是一道新题,又得从头再来,如何能让学生对所做的习题进行变通、推广,在不同角度、不同层次、不同情形、不同背景下重新认识呢?
于是,我对此题进一步研究,并查阅相关资料,对这道题进行不同的变换,在课堂上和学生一起讨论、交流,希望能起到举一反三的作用,同时也教给学生一种有效的复习方法。
一、掌握原题的基本方法
原题:如图2,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,连接EF,求证:EF=BE+FD
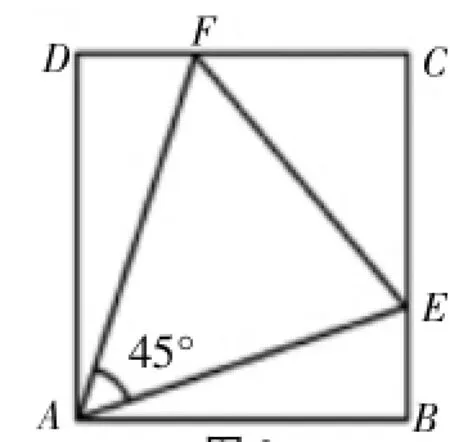
图2
引导学生归纳解决这一问题的方法:运用旋转,将△ABE和△ADF拼成一个三角形,通过证明三角形全等来证明结论。
二、对题目进行反思、探究
1.交换条件与结论,探究逆命题是否成立。学生运用刚才解决问题的方法,轻松得到结论,逆命题成立。
2.发散性思维训练,在原条件下,你还能得到哪些结论?
结合刚才的证明过程,学生还可以发现EA、FA分别平分∠BEF和∠EFD这一结论。
3.有了以上的发现,我给出了学生三个问题:
原条件不变,
(1)求证S正方形ABCD:S△EAF=2AB:EF。
(2)若BE=2,DF=3,求AB的长。
(3)若F是DC的中点,则tan∠AFE=,cos∠AEB=。
在解决问题(1)时。因为S四边形ABCD=AB2,易证△AEF中EF边上的高与正方形边长相等,即可证得结果,用到了EA平分∠BEF或FA平分∠EFD的结论。
在解决问题(2)时,用到了BE+FD=EF这一结论,设正方形的边长为x,用含有x的式子表示出△ECF三边,利用勾股定理列方程即可得到AB的长,更进一步引导学生在BE,FD,AB三边中已知其中两条,即可求得另一条,从而将这一求解过程一般化。
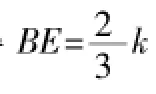
在这一过程中,通过补充相应的问题的条件,对原题进行了引申、发展、拓展,增加了问题的背景,增大了发散思维。
三、再对题目进行类比引申
只有正方形才有类似的结论吗?引导学生做以下变形:
引申一:
(1)如图3,四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在边BC、CD上,∠EAF=45°,若∠B和∠D都不是直角,∠B、∠D满足怎样的等量关系时,会有EF=BE+DF。
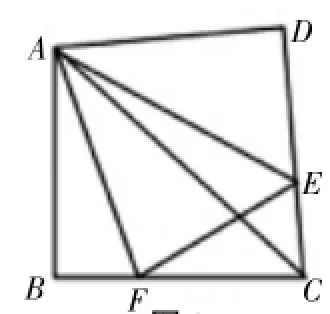
图3
事实是,当∠B+∠D=180°时,EF=BE+DF,分析其本质特征,经过旋转△ABE和△ADF能合成一个三角形,并且与△AEF全等,只要这一特征在,结论就成立,然后引导学生探究刚才的问题,∠B+∠D=180°的前提下,若EF=BE+DF,则∠EAF=45°成立吗?EA、FA还平分∠BEF和∠EFD吗?结论是肯定的。

图4
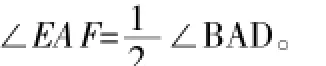
这一过程中,引导学生从特殊性到一般化,加强了学生思维能力的培养,也培养了学生分析问题的能力。
引申二:
若改变问题的背景,即将正方形变成三角形,结果又如何呢?为此设计了以下题目:
如图5,Rt△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,猜想BD、DE、EC应满足的等量关系,并写出推理过程。
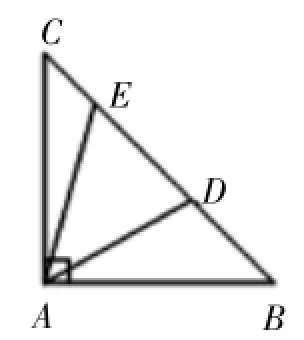
图5
在解决这一问题时,可以看到本质条件仍然在,即∠BAC= 90°,AB=AC,基本方法仍然适用。旋转△ABE,全等也依然要证明,只不过结论变成了DE2=BD2+EC2,这是由∠B+∠ACB=90°这一条件形成的。
通过对问题的引申,引发学生对问题的思考,抓住本质的内容,从中既体会到条件的变化,也体会到万变不离其宗,即解决问题的基本方法不变,进一步得到更为一般的结论,提高了学生的应变能力。
四、最后总结性的实践运用
经过一系列的学习、探究、引申,为检测学生对本节课所学知识的掌握情况,我设计了如下题目:
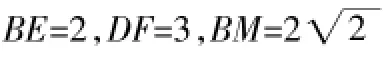
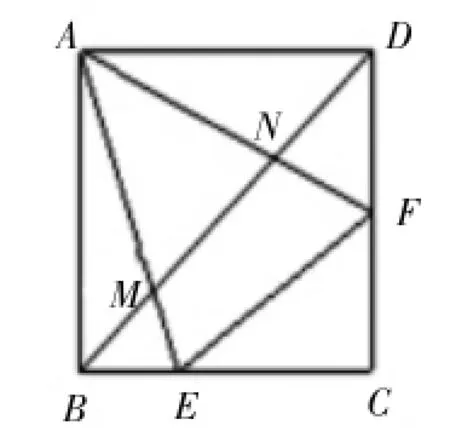
图6
解决这一问题时,既用到了正方形中,EF=BE+DF这一结论,又用到了直角三角形中MN2=BM2+ND2这一结论,巩固了所学,也提高了学生解决问题的能力。
通过这样的训练,学生眼里的题目不再是单独的一个点,而是一类,学到了一些数学方法,体会了一些数学思想,也了解了一个推向一般性的结论。
我想,在数学教学中,若将经典例题、习题充分揣摩,经常进行这样的反思、探究、引申,不但可以抓好基础知识,还可以激发学生的探究欲望,提高学生的创新能力。在纵横发散中,达到知识串联,综合沟通,起到举一反三的效果,从而提高了学生的综合分析能力和数学思维能力。
·编辑鲁翠红
