化归思想在初中数学教学中的运用

应素群

（浙江省台州市黄岩西城中学）

探索篇·方法展示

化归思想在初中数学教学中的运用

应素群

（浙江省台州市黄岩西城中学）

化归就是在研究和解决数学问题时采用某种方式，借助某种函数性质、图象、公式或已知条件等将问题通过变换使之转化，进而达到解决问题的一种思想。化归思想是中学数学最基本的思想方法，也是最重要的思想方法之一，在数学解题中几乎无处不在，它不仅是一种重要的解题思想，也是一种最基本的思维策略，更是一种有效的数学思维方式。应用化归思想解题时的原则是化难为易、化生为熟、化繁为简、化未知为已知，本文就谈谈化归的几种常用方法在数学解题中的运用。

一、数与形的转化

通过挖掘已知条件的内涵，发现式子的几何意义，利用几何图形的直观性化繁为简，从而解决问题。

乘法公式中的平方差公式（a+b）（a-b）=a2-b2的几何意义表述就是一个很好的例证，利用几何图形的面积完美地验证了公式的正确性。

例1.如下图，在边长为a的正方形中挖掉一个边长为b的小正方形（a＞b），再重新拼图，两图中的阴影部分面积分别为a2-b2和（a+b）（a-b），则可得到公式（a+b）（a-b）=a2-b2。

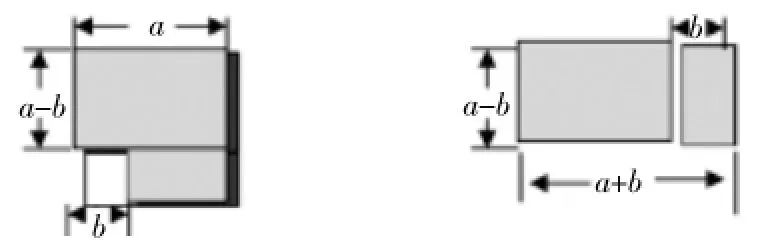
类似的，完全平方公式（a+b）2=a2+2ab+b2也可用数与形的转化来验证。

数与形是数学研究的两大基本对象，由于坐标系的建立，使数与形互相联系，互相渗透，因此，函数问题中此种方法更常见，用函数图象来刻画函数解析式就是很好的例证。

二、函数与方程或不等式的转化

函数是中学数学的一个重要概念，它渗透在数学的各部分内容中，是用运动变化的观点分析和研究具体问题中的数量关系。方程和不等式则是两个不同的概念，但它们之间有着密切的联系。方程f（x）=0的解就是函数y=f（x）的图象与x轴交点的横坐标，不等式f（x）＞0的解集就是函数图象位于x轴上方时自变量的取值范围。要确定函数变化过程中的某些量，经常要转化为求出这些量满足的方程或不等式的解或解集，函数是变量的动态研究，而方程不等式是动中求静，研究运动中的变量关系。

例2.二次函数y=ax2+bx+c（a≠0）的部分图象如下图，请根据图象回答下列问题：

（1）写出方程ax2+bx+c=0的两个根；

（2）写出x为何值时，y的值大于0；

（3）若方程ax2+bx+c=m没有实数根，求m的取值范围。

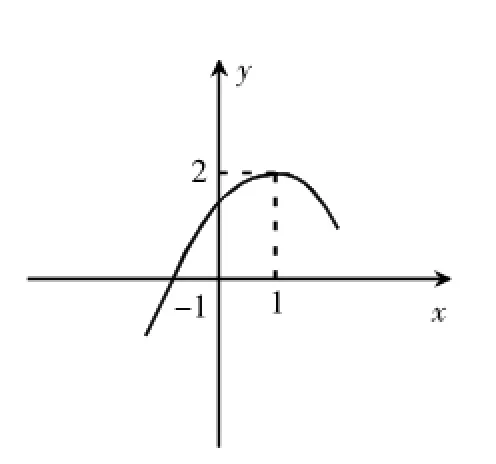
解析：（1）图象的顶点坐标（1，2）与x轴的一个焦点坐标为（-1，0），根据抛物线的对称性，可得与x的另一个交点坐标为（3，0），可得方程ax2+bx+c=0的两根为x1=-1，x2=3；（2）根据图象把不等式问题转化为函数图象在x轴上方时x的取值范围，易得-1＜x＜3；（3）可以把问题转化为求抛物线y=ax2+bx+c与直线y=m无交点时，m的取值范围。由图象可直观地得到m＞2，把复杂的问题简单化，把方程或不等式问题转化为函数图象问题，从而解决问题。此类问题也体现了数与形的转化和统一，数学的美无处不在。

三、特殊与一般的转化

对于那些结论不明或解题思路不易发现的问题，可先用特殊情形探究解题思路或命题结论，再在一般情况下给出证明。

例3.已知下面一列等式：

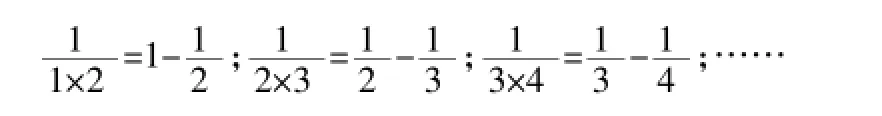
①请根据这些等式的结构特征写出它的一般性等式，并验证你写出的等式是否成立；

一般成立，特殊也成立。特殊可以得到一般性的规律，一般性的规律用来解决特殊问题，这种辩证思想在初中数学中普遍存在，经常运用，这也是化归思想的体现。

四、等与不等的转化

等与不等的转化主要是化相等为不等和化不等为相等，在等与不等的矛盾转化中基本不等式、方程思想、函数的性质经常发挥着重要的作用，它们是等与不等关系差异的联系所在。

例4.已知正实数a、b满足ab=a+b+8，则a+b的最小值为。

解析：根据基本不等式（a+b）2≥4ab，得（a+b）2≥4（a+b）+32，令x=a+b，则x-4x-32≥0，x≥8或x≤-4（舍去），所以a+b的最小值为8。

解析：根据平方根的意义，有x-1≥0和1-x≥0成立，于是得到x=1这一等式的成立，把不等关系转化相等关系，求得y=3，于是有xy=13=1，问题得解。

相等关系与不等关系既是对立统一的，又是相互联系的，在一定条件下可以互相转化，把复杂的问题简单化，也体现了数学的对称美和统一美。

五、正与反的转化

解题一般是从正面着手，习惯于正向思维，对于那些从正面很难解决的问题，不妨从其反面入手，从而使正面问题得以解决，此法也称为逆向思维。

例5.求证：三角形的三个内角中至少有一个不大于60°。

解析：要解决本题，从正面着手有困难，此时可以从反面“三角形的三个内角都大于60°”着手，引出与“三角形三个内角和为180°”这一定理相矛盾，从而反面不成立，即正面成立，问题得解。

此法亦称反证法，我们假定结论不成立，即结论的反面成立，经过推理论证，得出与已知条件或公理、定理相矛盾的结论，从而得出假设错误，亦即原命题成立的结论。

六、高维与低维的转化

物体的空间形成，总是表现为不同维数且遵循由低维向高维的发展规律，通过降维转化，可把问题由一个领域转换到另一个领域而得以解决，这种转化在初中数学的几何中比较常见。

例6.如下图，圆柱的底面半径为6 cm，高为10 cm，蚂蚁在圆柱表面爬行，从点A爬到点B的最短路程是多少厘米（结果保留小数点后一位）？

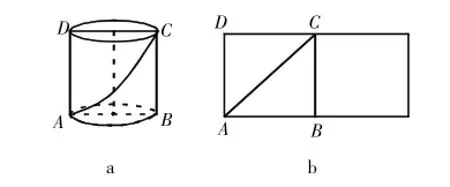
解析：图a是立体图形中的问题，路径是一条曲线，把圆柱的侧面展开成图b，不难发现，最短路程即为线段AC的长，于是有

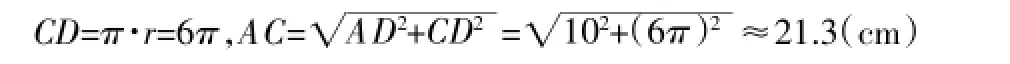
此类空间路径最短问题，可通过立体图形的侧面展开图将其转化为平面上的路径最短问题，利用“两点之间线段最短”来解决，即把高维向低维转化，从而解决问题。

除此之外，还有很多知识之间都存在着相互渗透和转化，比如多元转化为一元、高次转化为低次、分式转化为整式、多边形转化为三角形等，化归在数学解题中几乎无处不在，它渗透了数学教学的各个领域和解题过程的各个环节，掌握好化归的技能和技巧将大大提高解题的速度和质量。

［1］张柏.化归思想在初中数学教学中的渗透与应用［J］.新课程（下），2013（4）.

［2］况玲.化归思想在初中数学教学中的应用［J］.数学学习与研究，2016（14）.

·编辑鲁翠红