圆锥曲线切点弦中点的轨迹方程

■广西恭城县恭城中学　韦兴洲



圆锥曲线切点弦中点的轨迹方程

■广西恭城县恭城中学韦兴洲

一、问题探索

若自平面内一点引圆锥曲线的两条切线，则连接切点的线段称为切点弦.

设点M（x0，y0）为曲线Γ1：f（x，y）=0上的动点.

问题1：若过点M可以作圆锥曲线Γ2的两条切线，则点M的位置如何？

问题2：若过点M可以作圆锥曲线Γ2的两条切线，则切点弦中点的轨迹方程如何？

笔者通过对上述两个问题的探究，获得公式化结论如下表：

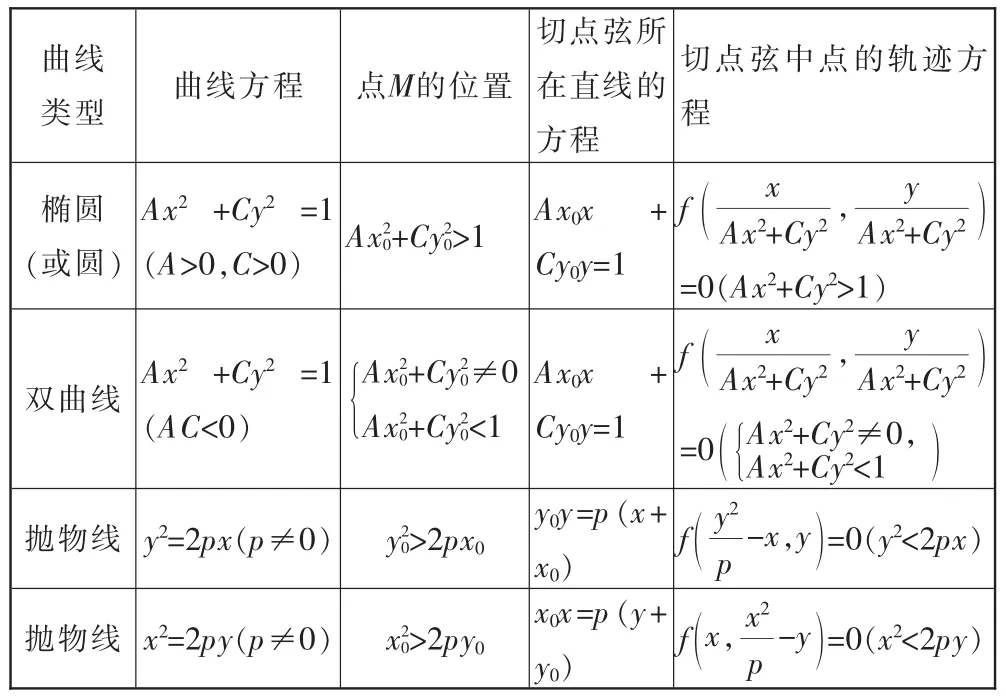
曲线类型　曲线方程　点M的位置切点弦所在直线的方程切点弦中点的轨迹方程椭圆（或圆）Ax2+Cy2=1 （A＞0，C＞0）　Ax20+Cy20＞1　Ax0x　+ Cy0y=1 fx Ax2+Cy2，　y Ax2+Cy2（=0（Ax2+Cy2＞1）双曲线Ax2+Cy2=1 （AC＜0）Ax20+Cy20≠0 Ax20+Cy20＜｛1Ax0x　+ Cy0y=1 fx Ax2+Cy2，　y Ax2+Cy2（=0Ax2+Cy2≠0，Ax2+Cy2＜｛1（）抛物线y2=2px（p≠0）　y20＞2px0y0y=p（x+ x0）　fy2p-x，（）y=0（y2＜2px）抛物线x2=2py（p≠0）　x20＞2py0x0x=p（y+ y0）　f x，x2p-（）y=0（x2＜2py）

以双曲线的情形为例，证明如下.

设过点M作双曲线Ax2+Cy2=1（AC＜0）的两条切线所得切点为G（x1，y1），H（x2，y2），根据隐函数求导法则，方程Ax2+Cy2=1两边同时对x求导，得Ax+Cyy′=0，从而故双曲线在点G处的切线方程为，由于点G在双曲线上，即代入切线方程并化简得Ax1x+Cy1y=1.又因为点M（x0，y0）在切线上，所以Ax1x0+ Cy1y0=1①.同理得Ax2x0+Cy2y0=1②.比较①②得切点弦所在直线的方程为Ax0x+Cy0y=1.

当AC＜0时，直线Ax0x+Cy0y=1与双曲线Ax2+Cy2=1有两个交点方程组有两组解方程有两个相异实根⇔

又设切点弦的中点为N（x3，y3）.联立Ax0x+Cy0y=1， Ax2+Cy2=1，得，可得即故④，代入③得计算得x0=代入④得结合点M（x0，y0）在曲线Γ1：f（x，y）=0上，可得点N在曲线上.又根据得

当圆锥曲线为椭圆（或圆）和抛物线时，可类似讨论，不再赘述.

二、结论应用

利用上述公式化结论，我们可重新求得文1中的轨迹1.

也可重新求得文1中的轨迹3、轨迹5和轨迹6，以及文2中的椭圆及其伴圆的性质6，双曲线及其伴圆的性质6.感兴趣的读者可自行查阅.

我们还可以利用上述公式化结论研究2013年高考辽宁卷理（文）科数学第20题.

题目如图1，抛物线C1：x2=4y，C2：x2=-2py（p＞0），点M（x0，y0）在抛物线C2上，过M作C1的切线，切点为A、B（M为原点O时，A、B重合于O），，切线MA的斜率为

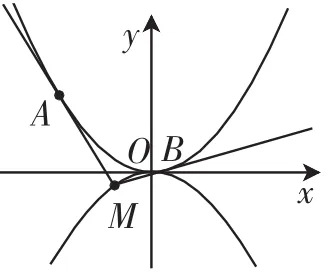
图1

（Ⅰ）求p的值；

（Ⅱ）当点M在C2上运动时，求线段AB的中点N的轨迹方程.（A、B重合于O时，中点为O）.

参考文献：

1.玉云化.椭圆、双曲线与相关圆生成的轨迹方程［J］.数学通讯（下），2012（1）.

2.林风.圆锥曲线伴圆性质的探究［J］.中学数学研究（南昌），2012（3）.F