基于R软件对股票时间序列模型分析

陈锦扬

摘要：本文通过R软件对机器人股票五年的数据进行分析，建立ARIMA模型分析该股的报酬率，发现该股在期间内报酬稳定增长，是适合长期投资的股票。同时建立协整模型和误差修正模型，分析长期和短期指标间对报酬率的影响，最高价、最低价和市销率的系数均为正且显著，短期市净率不在对股票报酬有影响。

关键词：单整阶数 平稳检验 报酬率

随着国家经济的转型，大数据分析已经越来越重要。而股票市场是国家经济的晴雨表，股市的走势直接反映出经济的运行情况，为了研究国家高尖端机器人领域的股票走势情况。本研究采用机器人股票从2009年11月到2015年11月的数据。总共有1456天的数据。通过R软件的运用，建立ARIMA模型分析该股票的报酬率，并通过协整模型分析哪些指标因素对报酬率有影响，同时建立相应的误差修正模型分析短期影响。

一、时间序列原理

（一）ARIMA模型

模型是将时间序列数据视为—个随机序列.以时间序列的自相关分析为基础.用模型来近似描述这个序列。这个模型一旦被识别后就可以从时间序列的过去值及现在值来预测未来值。ARIMA模型在经济预测过程中既考虑了经济现象在时间序列上的依存性，又考虑了随机波动的干扰性，对于经济运行短期趋势的预测准确率较高。

ARIMA（p，I，q）模型公式定义为：

[Xt=φ1Xt-1+.....+φpXt-p+wt+θ1wt-1+.....+θqwt-q]

（二）协整模型

如果两个或两个以上的时间序列有相同的单整阶数，且某种线性组合使得组合时间序列的单整阶数降低，则称这些时间序列之间存在显著的协整关系。所谓协整关系可理解为两变量间具有长期稳定关系。

其公式定义为：[z=（x1，...xn+xn+1）T，x1～I（d），i=1，2，...，n+1]

若存在某一向量：[αT=（α1，...，αn+1）T]，使得[αTz～I（d-b），b>0]

则称[αTz=α1X1++αnXn+αn+1Xn+1]为系统z的协整关系。

二、股票的实证分析

（一）报酬率的数据平稳性判定

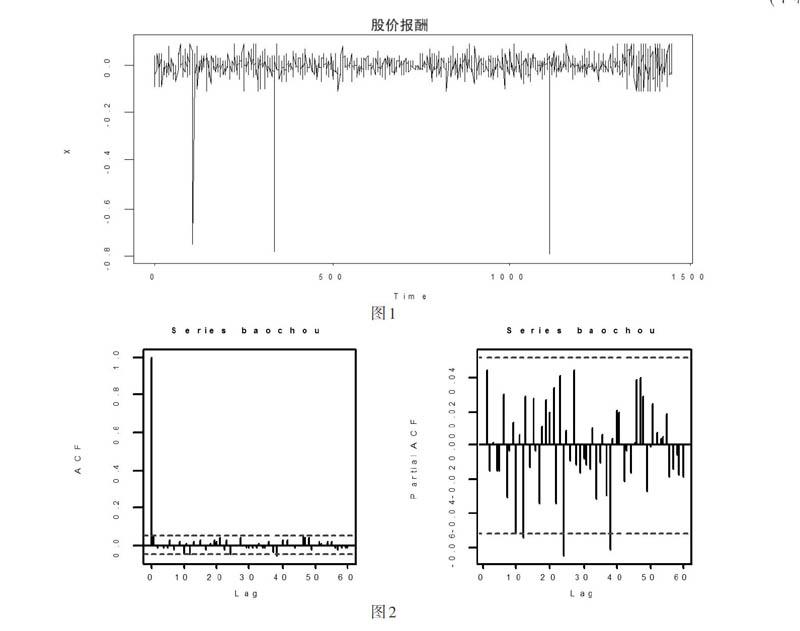
本研究采用自然对数的方法计算机器人股票的股价报酬率，计算方式是每日收盘价价FUPt 的对数差分再乘以100，即RFUPt =100*[ln（FUPt）-ln（FUPt-1）]，对股价报酬率画走势图。 见图1。

上图说明机器人的股价报酬率走势比较稳定，大的波动不多，基本在零左右上下波动。对其做单位根检验，其P-value值<0.01，显著说明股价报酬率是稳定的时间序列。

（二）ARIMA模型的建立

对股价报酬率做acf、bcf分析，如图2所示。

根据acf和bcf图对ARMA模型阶数进行判断，发现ARMA（1，0，0）比较适合。

模型统计结果为：

[RFUPt=0.0001（0.0013）+0.0443（0.0262）RFUPt-1]，t取值（1，2，...n）

模型的指标-2l（likelihood）=2320.93，AIC=-4637.该模型在相应数据下拟合良好。对其做Garch模型的检验，发现P-value均大于0.05，拒绝Garch模型的建立。

（三）股票价格的协整模型

通过对数据的平稳性检验发现 ，具有相同一阶阶差分平稳的指标有x1为最高价、x2为最低价、X3为市净率、x4为开盘价、x5为成交量、x6为市销率等指标。建立线性回归模型为：

[Y=-0.417+0.633X1+0.901X2-0.022X3-0.528X4-0.167X5+0.0550X6] （2）

（-5.06（23.65）（31.94）（-1.681（-20.276）（-2.81） （4.86）

系数P值均通过检验，但模型是否合理，我们用Johansen协整检验来对模型进行检验，检验结果表明r<=6通过检test=1.22，10pct=7.25，5pct=9.24，1pct=12.97.模型设定的六个指标均通过协整检验。模型（2）中最高价、最低价和市销率的系数均为正且显著，说明这三个指标对收盘价有正的效应。最低价的系数最高为0.901，说明该股的每日的最低价不能太低，否者会严重影响收盘价。市净率、开盘价和成交量均为负且显著，说明这三个指标对每日的收盘价有负效应。其中开盘价最高，说明当股票高开之后，很大概率以低价收盘，在长期这只股票是比较稳定的一直股票。

（四）误差修正模型

在对模型做误差修正模型，得到的回归模型为：

[Δy=-0.0047+0.619Δx1+0.643Δx2-0.462Δx3-0.0897Δx4-0.441Δx5+0.369Δx6+1.012εt-1]（3）

统计结果显示除[Δ]X3的统计量p值=0.272不显著，其他变量均显著，拟合优度为R2 =0.903说明模型拟合显著。在短期内市净率对股票收盘价没有显著影响，这个结论非常符合现实，市净率是市净率指的是每股股价与每股净资产的比率。在短期内，股票已经选定的情况下，市净率将不会再影响股票的价格。[εt-1]的系数为正且显著，说明在短期内前一天的股票指标还会影响今天的收盘价格，而且影响很大。

三、结束语

本文实证研究了机器人股票的数据指标间的关联性，协整检验表明，在长期每日收盘价受当日开盘价、最高价、最低价、市净率、市销率和成交量的影响很大，但在短期，根据误差修正模型，市净率对该股票的影响不显著。该股的ARIMA（1，0，0）模型表明酬率时间序列很平稳，如果前一天的收益每增加一个单位，后一天的收益率也很可能增加0.0443个单位，从中说明该股一直处于上涨的趋势中，适合长期投资。

参考文献：

[1]马超群，李科.基于协整和GARCH模型分析[J].求索，2004.12

[2]洪萬吉，楊永列，程淑樺，黃美裕.对富邦金融控股公司之股票市场报酬的风险因素分析[N].正学修报，2006.19

[3]林茜.中国股价行为相关性与协整性的实证研究[D].辽宁：东北财经大学，2006.10