子弹撞击Hopkinson杆的应力误差分析
2016-03-30朱倩倩尤文斌范锦彪
朱倩倩,尤文斌,范锦彪
(1.中北大学电子测试技术国家重点实验室,山西太原030051;2.中北大学仪器科学与动态测试教育部重点实验室,山西太原030051)
子弹撞击Hopkinson杆的应力误差分析
朱倩倩1,2,尤文斌1,2,范锦彪1,2
(1.中北大学电子测试技术国家重点实验室,山西太原030051;2.中北大学仪器科学与动态测试教育部重点实验室,山西太原030051)
摘要:针对在Hopkinson杆的中间对称位置放两片应变片测得时间-应力曲线不同的问题,采用ANSYS/LS-DYNA有限元分析软件建立子弹撞击小杆的实验模型;通过仿真得到沿着杆轴向不同位置的时间-应力曲线,该曲线的变化趋势和平头弹撞击Hopkinson杆实验数据得到的实测时间-应力曲线变化趋势一致,得出压力变化越快,应变率越大,导致应变快,相应的应力增大快的结论。由于应力波的衰减与弥散,前应变片测得的应力总是大于后应变片。
关键词:Hopkinson杆;ANSYS/LS-DYNA软件;时间-应力曲线;应变率
0 引言
Hopkinson压杆实验中的应力状态是一维应力,实验过程中波形易于控制,入射波(压力脉冲)和来自自由面的反射波(拉伸脉冲)较易测到[1]。但当持续时间大于L/C(L为入射杆的总长度,C为弹性波波速)时,会导致入射杆中间应变片上获得的入射应变波形和反射应变波形叠加。
目前,对叠加波形分离研究,主要是采用在入射杆的2个不同位置粘贴应变片的方法。这种方法最早是由Lundberg与Henchoz分别提出的,H.Meng 和Q.M.Li在他们的基础上,建立了应用于分离式霍普金森压杆(split Hopkinson pressure bar,SHPB)系统中的两应变片测试技术[2],采用两片应变片同时测量物体的应力,以便得到更精确的测量结果。
SHPB试验技术有两个基本假定,即压杆一维应力波假定和事件均匀性假定[3-4]。但是,由于应变片材料本构关系以及应力波在杆中的衰减与弥散的影响,往往两片应变片测量得的应力曲线不一致。
本文利用ANSYS/LS-DYNA有限元分析软件建立Hopkinson杆模型,模拟得到不同位置的时间-应力曲线,并与实测曲线进行比较,分析出两个曲线不同的原因,为实测曲线的处理提供一定的理论依据。
1 材料模型及参数
针对在Hopkinson杆的中间对称位置放两片应变片,同时测量物体的应力,得到不同时间-应力曲线的现象。在ANSYS中,用刚性材料的钢仿真平头弹,及塑性材料的钢仿真小杆,让子弹以30m/s的速度去撞击小杆。被撞小杆受到压力,产生应变,经处理得到它的应力。
1.1子弹的材料模型
仿真中弹丸采用刚性材料模型,模拟实测实验中的平头弹。具体参数如表1所示。

表1 子弹(钢)的材料模型参数
1.2Hopkinson杆的材料模型
本文中,Hopkinson杆采用Mat_Johnson_Cook材料模型,该模型的表达式为
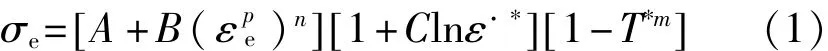
式中:σe——流动应力;
εpe——等效塑性应变;
ε.*=εpe/ε.0——相对等效塑性应变率,取ε.0=1.0s-1;
T*=(T-Tr)(Tm-Tr)——无量纲温度,其中,Tm和Tr为材料的熔点与室温。
上式中第1个因子给出的是当ε.*=1.0和Tm=0时流动应力与等效塑性应变的函数关系。第2个和第3个因子表示了应变率效应和温度效应[5-6]。模型中的经验型材料参数A为参考温度和参考应变率下材料的屈服应力,常数A、B和n反映了材料的应变硬化特征,C反映了应变率对材料性能的影响,m反映温度软化效应[5]。
杆的材料也是钢,采用Johnson_Cook塑性模型,该模型主要参数如表2[7]所示。

表2 Hopkinson杆的材料模型参数
2 仿真实验
2.1仿真模型
用ANSYS/LS-DYNA有限元分析软件建立子弹撞击小杆的实验模型。其中,子弹尺寸为:φ1.4 cm× 2cm,小杆尺寸为:φ1.4cm×40cm。用三维实体单元solid164进行网格划分,采用cm-g-μs单位体系。为了减少计算工作量,利用结构和载荷的对称性,建立1/4有限元模型,如图1所示。
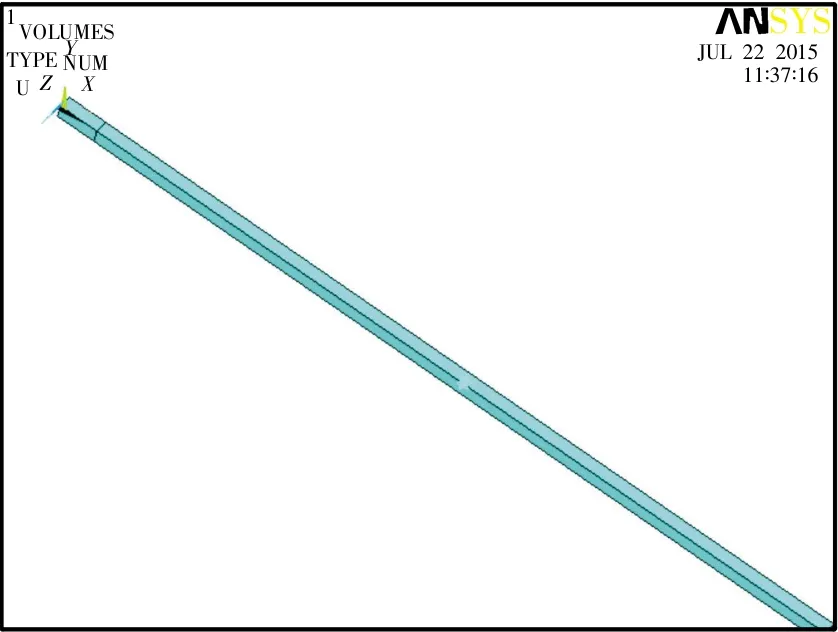
图1 仿真模型图
2.2仿真结果
让子弹以30m/s的速度去撞击小杆,历时80s。在软件LS-PrePost中观察撞击结果,发现杆上有应力波从子弹这一端向着另一端传播,且杆的应力有一个由小到大再逐渐减弱的过程。
沿着杆的轴向,取A、B、C 3点,分别间隔0.5cm。该模型中,X轴即为杆的方向,其他方向已经被约束不产生应力,对结果的影响可忽略不计,则可画得X轴方向的时间-应力曲线,如图2所示。
由图可得,A、B、C 3点应力峰值依次减小,且A点应力增大最快,B点次之,C点最慢。其中A点在时间16 μs处,达到了最大值171 MPa;B点在20μs处达到了最大值117 MPa;且C点在24μs处达到了最大值79 MPa。
3 实测实验
3.1实验装置
本文使用Hopkinson杆,对应变片的材料本构特性进行了研究。实测实验中,子弹是用2cm的平头弹,用一定的压力撞击小杆。在杆的中间位置,对称放置两片相隔5cm的应变片,实验原理如图3[8]所示。
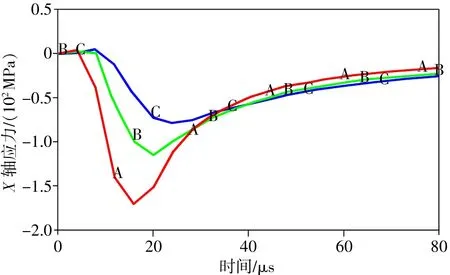
图2 杆轴向的时间-应力曲线
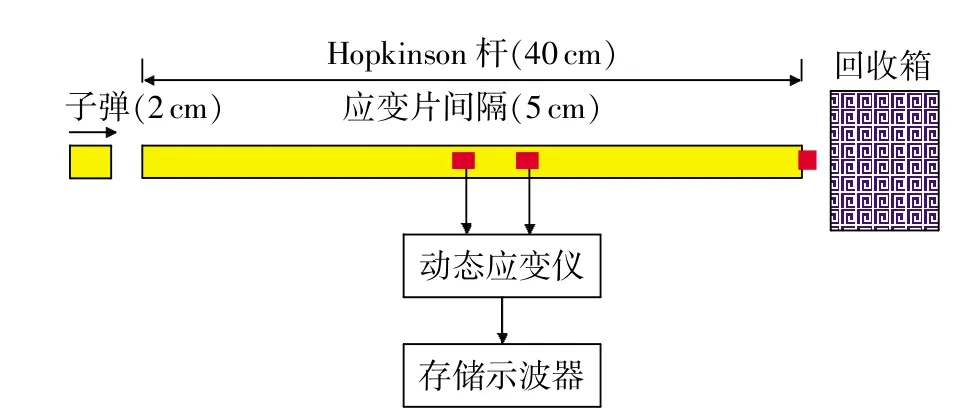
图3 Hopkinson杆原理图
在常温环境下,将被测芯片用工业黄油吸附在钢制Hopkinson杆的尾部,用压缩氮气发射一粒长为2 cm、直径为1.4 cm的钢制子弹,同轴撞击长为40cm、直径为1.4cm的钢质Hopkinson杆的另一端。
3.2结果与分析
3.2.1实测结果
为了确定应变片的电压信号和应变之间的对应关系,首先要对超动态应变仪进行校准。记校准阶跃高度为X,对应的应变为Xg。在冲击实验时,如果应变片经超动态应变仪放大后的输出信号为Ug(t),那么对应的应变[5]为
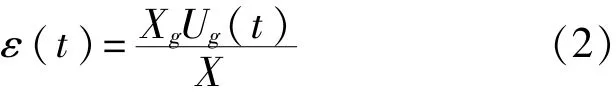
由于:

所以应力:
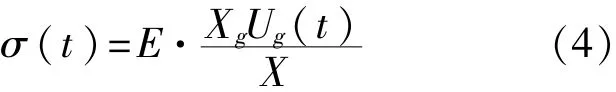
将存储示波器的数据调入Matlab处理,得到0.05 MPa和0.1 MPa脉冲压力下,两组应变片的时间-压力曲线,分别如图4、图5所示。放在前面的应变片,测得的数据称为前应力(图中曲线A),而后面的应变片测得的数据称为后应力(图中曲线B)。
3.2.2比较与分析
由图4和图5可得,不论脉冲压力的大小,前应力上升速度总是比后应力速度快,且前应力的峰值明显大于后应力。由误差=(前应力-后应力)/前应力×100%,计算可得误差如表3所示。
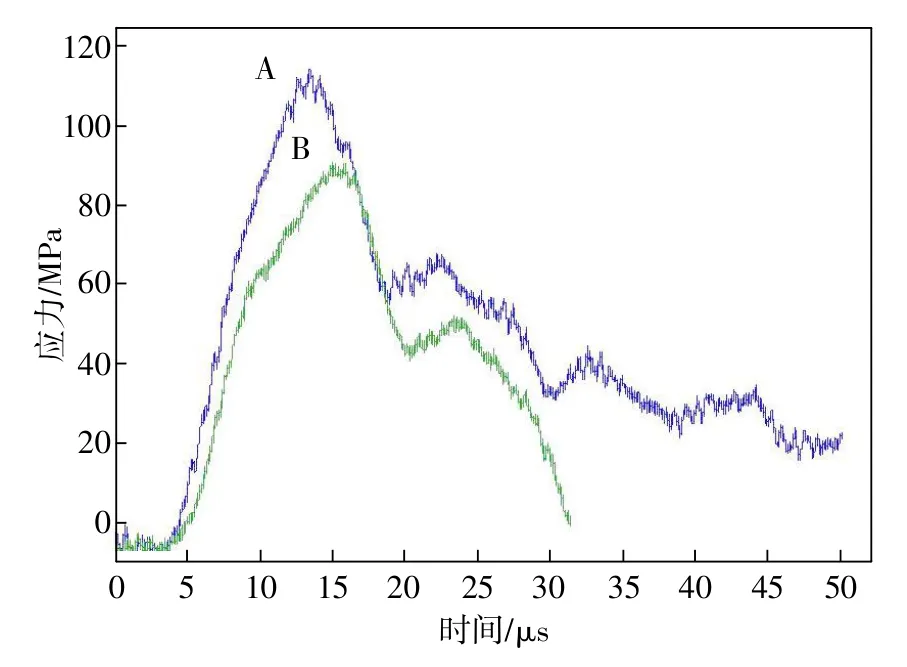
图4 0.05 MPa压力下的应力

图5 0.1 MPa下的应力

表3 前应力与后应力的误差
显然,实测的时间-应力曲线图和仿真得到的曲线图变化趋势一致。由式(1)分析可得,力在杆中的传播需要一个过程,A点(前应力)总是比B点(后应力)先接受到压力。施加同等压力,施加的速度越快导致应变片的应变率越大,则相应的应变大,应力增大快,即上升时间短。
这里,有两个因素影响应力的大小:
1)A点的应变率大,导致它的应变小,由式(3)可得A点的应力小于B点;
2)由于子弹撞击杆的力是一个脉冲压力,它产生的力波在传输过程中会逐渐衰减和
弥散,所以导致A点的压力比B点大,即A点的应力比B点大。
由仿真和实测结果皆可得,两个因素放在一起,后者占了主要作用,所以最后显示的结果A点应力(前应力)比B点(后应力)大。
4 结束语
ANSYS/LS-DYNA模拟仿真得到不同位置的时间-应力曲线与实测子弹撞杆的曲线趋势一致,说明:1)由于材料的本构关系,位置在前的应变片的应变率大,应变快,相应的应力增大快;2)由于应力波在杆中的衰减与弥散,位置在前的应变片测得的应力总是大于后应变片。同时用多个应变片测量应力的时候,应该将以上因素考虑到测量结果中。
参考文献
[1]胡时胜,张磊,武海军,等.混凝土材料层裂强度的实验研究[J].工程力学,2004,21(4):128-132.
[2]刘瑞堂,果春焕.改善Hopkinson压杆的波形分离技术[J].哈尔滨工程大学学报,2009,30(4):461-465.
[3]平琦,马芹永,袁璞. SHPB试验岩石试件应力平衡时间预估分析[J].振动与冲击,2013,32(12):55-60.
[4]平琦,马芹永,袁璞. SHPB试验中不同加载升时应力平衡时间对波阻抗比的敏感性[J].岩石力学与工程学报,2013,32(11):2128-2134.
[5]吕剑,何颖波,田常津,等.泰勒杆实验对材料动态本构参数的确认和优化确定[J].爆炸与冲击,2006,26(4):339-344.
[6]董菲,GERMAIN G E,LEBRUN J L,等.有限元分析法确定Johson-Cook本构方程材料参数[J].上海交通大学学报,2011,45(11):1657-1667.
[7]王泽鹏,胡仁喜,康士延,等. ANSYS13.0/Ls-DYNA非线性有限元分析实例指导教程[M].北京:机械工业出版社,2011:215.
[8]徐鹏,祖静,李乐. CPLD芯片抗高g值冲击性能分析[J].振动与冲击,2006,26(1):148-150.
(编辑:莫婕)
Stress error analysis of bullet impacting Hopkinson bar
ZHU Qianqian1,2,YOU Wenbin1,2,FAN Jinbiao1,2
(1. National Key Laboratory for Electronic Measurement Technology,North University of China,Taiyuan 030051,China;2. Key Laboratory of Instrumentation Science and Dynamic Measurement of Ministry of Education,North University of China,Taiyuan 030051,China)
Abstract:Two strain gauges put on the symmetrical position in the middle of a Hopkinson bar were measured to obtain different time-stress curves. As a result,the ANSYS/LS-DYNA finite element analysis software was used to build an experimental model for bullets hitting the bar. The time-stress curves in different positions along the stem direction were gained through simulation tests. The variation trend of these curves was consistent with that of the time -stress curves obtained through the experiment of head bullets hitting the Hopkinson bar. In conclusion,the faster the pressure changes,the greater the strain rate and the stress become. The measured stress of the former strain gauge is always larger than that of the latter one due to the attenuation and dispersion of the stress wave.
Keywords:Hopkinson bar;ANSYS/LS-DYNA software;time-stress curve;strain rate
作者简介:朱倩倩(1991-),女,江苏宿迁市人,硕士研究生,专业方向为动态测试与智能仪器。
收稿日期:2015-07-25;收到修改稿日期:2015-09-16
doi:10.11857/j.issn.1674-5124.2016.02.007
文献标志码:A
文章编号:1674-5124(2016)02-0033-03
