基于改进EMD和形态滤波的滚动轴承故障诊断

文　成，周传德

（重庆科技学院机械与动力工程学院，重庆401331）



基于改进EMD和形态滤波的滚动轴承故障诊断

文成，周传德

（重庆科技学院机械与动力工程学院，重庆401331）

摘要：针对滚动轴承故障振动信号的非平稳性特点，提出一种改进经验模态分解（EMD）和形态滤波相结合来提取故障特征信息的方法。该方法首先在原信号中加入高频谐波并进行EMD分解，减小传统EMD分解中存在的模态混叠现象，然后从高频本征模态分量（IMF）中去除高频谐波得到故障冲击成分，经形态滤波消噪后进行频谱分析，提取出故障特征信息。信号仿真分析该方法的实施过程，并将该方法成功运用于滚动轴承内圈和外圈故障的诊断。实验结果表明该方法能够有效提取滚动轴承故障特征信息，实现故障诊断。

关键词：改进经验模态分解；形态滤波；滚动轴承；故障诊断

0　引言

具有局部损伤类故障的滚动轴承在运行时会产生冲击性异常事件，振动信号为非平稳信号；因此，滚动轴承故障诊断的关键是如何从非平稳振动信号中有效提取反映特征信息的异常成分。经验模态分解（empirical mode decomposition，EMD）[1]是一种适用于非平稳信号的分析方法。EMD将信号分解成若干固有模态函数（intrinsic mode function，IMF）[2]，近年来在滚动轴承故障诊断中得到了广泛应用。然而，EMD方法存在模态混叠现象，易引起IMF分量失真[3]。文献[4]提出剔除异常数据法来抑制模态混叠，该方法只针对特定的异常信号，当异常事件为故障信息时无法提取特征信息。刘小峰[5]利用小波包对模态混叠的IMF进行分解并重构新的固有模态分量；但现场故障信号复杂，EMD处理后很难确定存在模态混叠的IMF阶次。Huang等[6]提出的总体平均经验模态分解（ensemble empirical mode decomposition，EEMD）成功解决了模态混叠问题，但分解效果与叠加的噪声水平和平均次数有很大的关系[7]，计算量过大，效率偏低。胡爱军等[8]采用叠加高频谐波后再进行经验模态分解的改进EMD方法，将异常事件限制在高频IMF中，从而改善了EMD分解质量，降低了模态混叠现象。文献[8]在没有噪声情况下研究了提取异常事件的方法，没有进一步阐述在噪声干扰下提高异常事件分析的准确度问题。当异常事件为故障信息时，就需要准确提取特征信息。通常高频IMF分量受噪声影响较大，直接进行频谱分析难以正确提取异常特征信息。因此，频谱分析前对高频IMF进行滤波是必要的。

数学形态滤波是一种非线性滤波方法，它的基本原理是利用移动结构元素来探测信号结构特征，从而达到抑制噪声和提取形状特征信息的目的。形态滤波弥补了线性滤波的不足，近年来在机械故障诊断中得到了广泛的应用，取得了较好的诊断效果[9-11]。

基于以上分析并结合滚动轴承故障特点，提出利用改进EMD和形态滤波相结合来提取滚动轴承故障特征信息的新方法。该方法首先用改进EMD方法对故障信号进行经验模态分解，得到冲击性异常事件的高频IMF分量，然后对高频IMF分量进行形态滤波，从而提取故障特征信息。实例表明，该方法可以有效提取滚动轴承故障特征信息，提高故障诊断的准确性。

1　基本理论

1.1改进EMD方法

EMD能将复杂信号分解成有限个不同尺度的固有模态函数之和，是一种自适应时变滤波过程。EMD分解效果与信号极值点及其分布有关，而冲击性异常事件往往导致信号极值点分布异常，造成模态混叠，难以反映信号的特征。

改进EMD方法能降低模态混叠现象，提高EMD分解质量，有效提取冲击性异常事件。改进EMD方法是将适当的高频谐波以线性叠加方法加入到原始信号中，然后再进行EMD分解。加入的高频谐波可以平滑异常事件，改变原始信号的极值分布，使信号包络更自然，从而提高EMD分解质量，降低模态混叠。EMD分解将信号从高频到低频分解成若干个IMF，第1个IMF往往是高频成分。由于冲击性异常事件（特征信息）是高频成分，所以高频谐波加入后再进行EMD分解可使异常事件限制在第1个IMF中，用第1个IMF减去加入的高频谐波即可提取特征信息。

设信号为x（t），改进EMD方法计算步骤如下：

1）将高频谐波x0（t）加入到原信号x（t）中，得到信号xm（t）：

2）对xm（t）进行EMD处理，分解得到若干个固有模态函数分量ci（t）与残余项r（t）。信号xm（t）可表示为

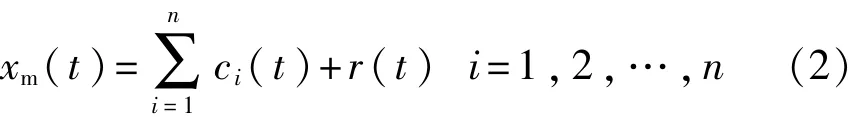
3）计算第1阶模态分量c1（t）（即IMF1）与高频谐波x0（t）的差，得到含异常事件的信号x1（t）。

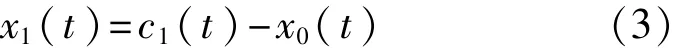
改进EMD方法的关键是确定待加入的高频谐波信号。如果高频谐波频率高于异常成分的频率，且幅值在原始信号峰值附近，那么高频谐波加入后将改变信号的包络分布，使EMD分解后将异常事件限制在第1个IMF（IMF1）中，从而提高EMD分解准确度，抑制模态混叠。

1.2形态滤波

形态滤波是数学形态理论在信号处理方面的重要应用。形态滤波通过特定的结构元素去探测信号，对信号进行各种形态变换，达到提取信号、抑制噪声的目的。形态变换包括膨胀、腐蚀、开运算和闭运算4种基本运算。

设信号x（n）和结构元素g（n）分别为定义在X= （0，1，…，N-1）和G=（0，1，…，M-1）上的一维函数，且N≥M，x（n）关于g（n）的膨胀、腐蚀、开运算和闭运算分别定义为

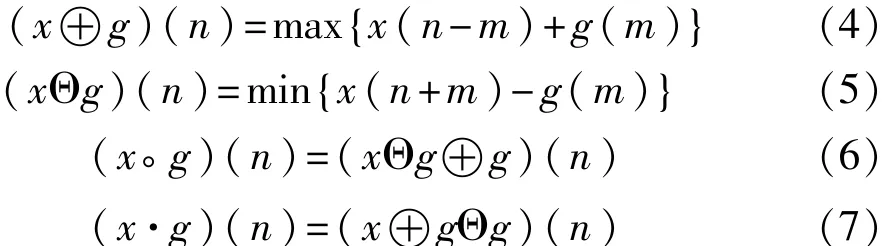
式中n∈[0，N-1]，m∈[0，M-1]，符号“⊕”、“Θ”、“。”和“·”分别表示膨胀、腐蚀、开运算和闭运算。

形态滤波是上述4个算子的各种组合运算。开运算和闭运算组合形成的闭-开形态滤波器兼有闭运算和开运算的优点，本文采用闭-开滤波器对滚动轴承故障进行研究。闭-开滤波器定义如下：

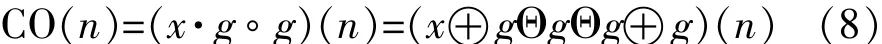
形态滤波效果与结构元素的形状和尺度有很大关系。直线型结构元素形状简单、计算量小且能完整地保留振动信号的特征信息，故本文采用直线型结构元素对改进EMD分解的高阶IMF进行形态滤波，提取出滚动轴承故障信息。

1.3改进EMD和形态滤波的信号分析方法

改进EMD和形态滤波信号分析流程如图1所示。首先将高频谐波x0（t）加入到故障信号x（t）中形成信号xm（t），对xm（t）进行EMD分解，得到有限个本征模态分量；然后将高频本征模态分量IMF1减去叠加的高频谐波x0（t），提取出含异常事件的特征信号x1（t），再经形态滤波得到xn（t）；最后对xn（t）进行频谱分析，即可提取异常事件，从而获得故障特征信息。

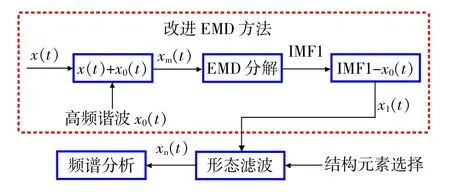
图1　改进EMD和形态滤波的信号分析流程图

2　信号仿真

以仿真信号x（t）为例，介绍改进EMD和形态滤波的信号分析过程。x（t）由低频正弦信号s1（t）与异常事件s2（t）叠加而成：

式中s1（t）=sin（20πt），s2（t）=0.1sin（200πt1）+0.2sin （200πt2），异常事件分别发生在0.3～0.36 s和0.6～0.66s处。

图2为信号x（t）直接进行EMD分解结果，其中，图2（c）为仿真信号x（t）时域波形；图2（d）～图2（f）为EMD分解得到的前3阶固有模态分量IMF1-IMF3，模态混叠现象十分明显，信号s1（t）与异常事件s2（t）均没有分解处理，分解质量很低。

图3为采用改进EMD方法分解信号x（t）的结果。图3（a）为叠加的高频谐波x0（t），图3（b）为原信号x（t）叠加x0（t）后得到混合信号xm（t）。对xm（t）进行EMD处理，图3（c）～图3（e）得到1～3阶固有模态分量IMF1-IMF3，显然IMF2就是s1（t），低频正弦信号被正确分解出来。图3（f）为IMF1减去高频谐波x0（t）得到的x1（t），明显看出x1（t）与s2（t）高度相似，即异常事件也被有效提取出来。对比可知，改进EMD方法可以减小模态混叠现象，提高了EMD分解的准确度。

现场采集的信号往往含有丰富的噪声成分，为考察噪声对改进EMD分解质量的影响，在原信号x（t）中加入有效值为0.05的随机噪声，得到图4（a）所示信号xs（t）。图4（c）～图（d）分别为xs（t）经改进EMD分解得到的IMF1和IMF2，显然，s1（t）在IMF2中被分解出来。图4（e）为IMF1减高频谐波后得到的信号x1（t），图中能够看出含有异常事件s2（t），由于噪声的干扰，s2（t）并不突出。图4（f）所示的信号xn（t）是x1（t）经闭-开形态滤波而得到的，显然，异常事件s2（t）已经非常明显。由此可见，改进EMD和形态滤波相结合的方法可以明显提高信号分析准确度。

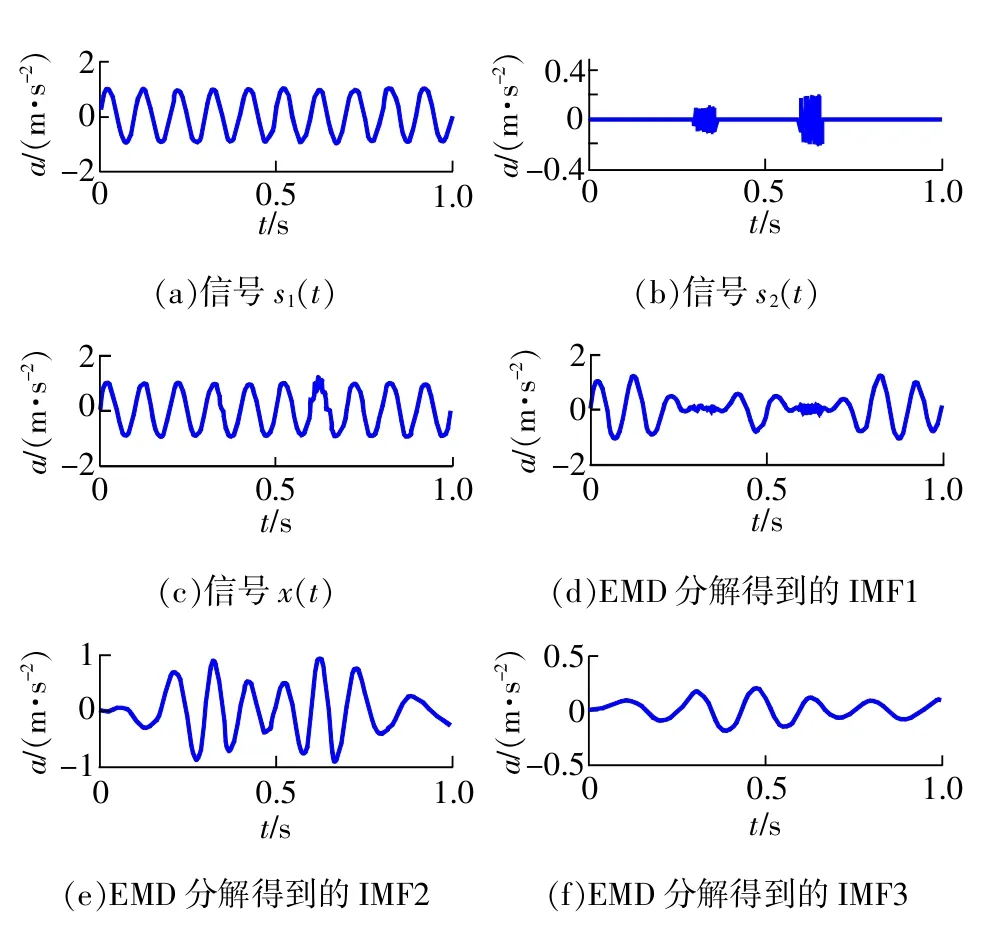
图2　信号x（t）直接EMD分解结果

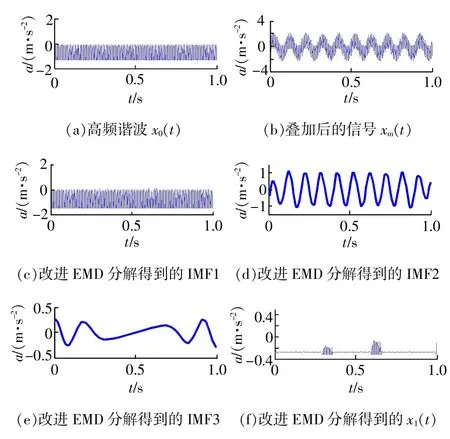
图3　信号x（t）改进EMD分解结果

3　工程应用

采用Case Western Reserve University提供的6203-2RS深沟球轴承现场振动信号，轴承节圆直径为28.5mm，滚珠直径为6.75mm，滚珠数为8。轴承故障利用电火花加工技术形成局部缺陷，故障直径为0.53mm。利用加速度传感器拾取电机壳体风扇端轴承振动信号，采样频率12kHz，分析长度为2048个采样数据点。在转速1750r/min工况下，分别测得内、外圈故障信号。由轴承几何参数和电机转速计算出内、外圈理论故障频率分别为fi=144.28 Hz和fo= 89.054 Hz，轴承内圈转频为fs=29.2 Hz。

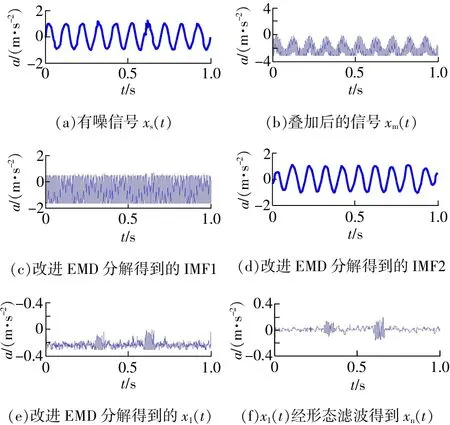
图4　有噪信号xs（t）改进EMD分解结果

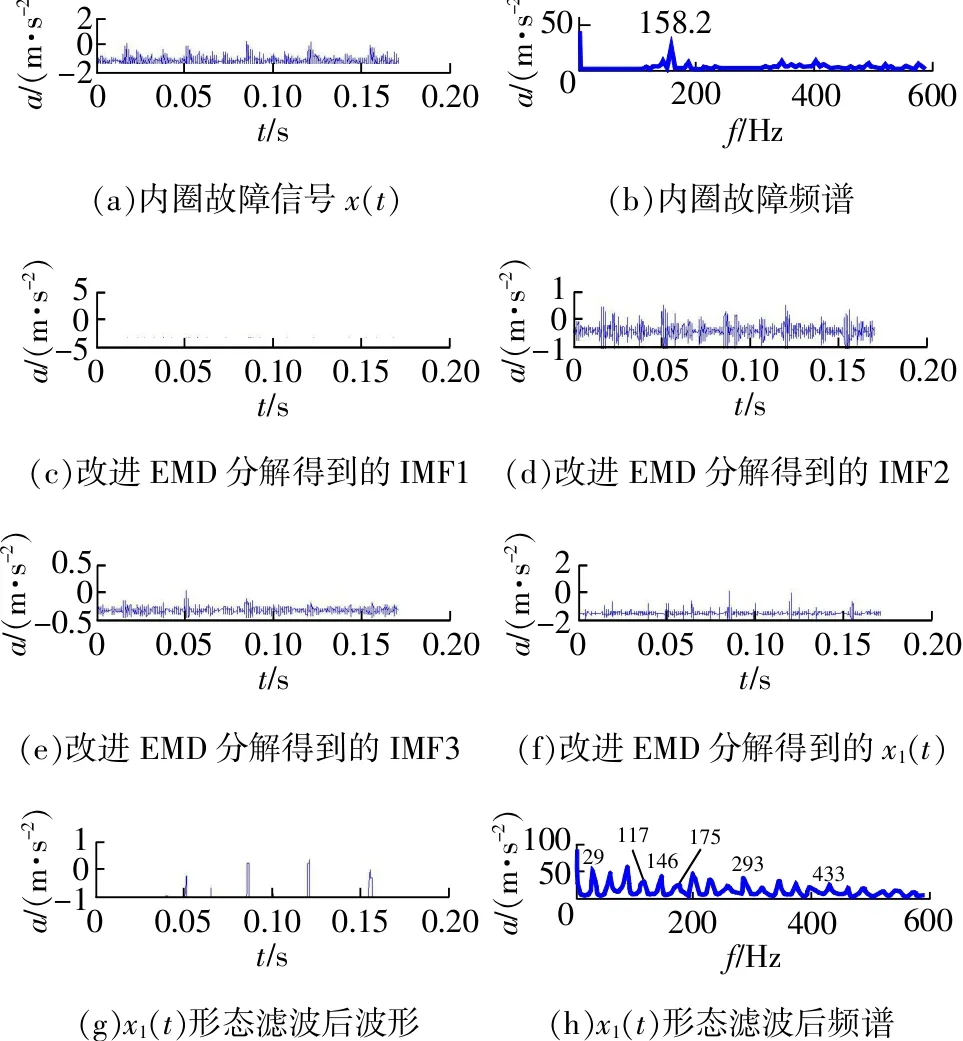
图5　内圈故障基于改进EMD和形态滤波分析结果

利用改进EMD和形态滤波方法对滚动轴承内圈故障信号进行分析，结果如图5所示。图5（a）和图5（b）分别为故障信号时域波形及其频谱图，频谱中158.2Hz与特征频率相差甚远，故障信息完全被噪声所淹没。图5（c）～图5（e）是改进EMD分解得到的前3阶模态分量，IMF1减去高频谐波后得到图5（f）所示异常事件x1（t）。图5（g）和图5（h）分别为冲击异常信号x1（t）经形态滤波后的时域波形及其频谱图，频谱中146Hz十分明显，这与内圈特征频率fi（144.28Hz）一致。在146 Hz两侧存在清晰的边频117 Hz和175 Hz，其中117≈fi-fs，175≈fi+fs，这是内圈特征频率与转频fs（29.2 Hz）调制而成。图5（h）中同时还有故障频率146 Hz的二倍频293 Hz、三倍频433 Hz以及以这些频率为中心的边频成分，边频成分之间间隔均为转频fs。由此可见，内圈故障特征十分明显，故障特征信息已完全提取出来。

图6为轴承外圈故障利用改进EMD和形态滤波方法分析结果。直接对原始信号作频谱分析，结果如图6（b）所示，故障特征频率成分fo完全消失。图6（h）是利用本文提出的方法得到的频谱结构，其中突出谱线87.9 Hz与外圈故障特征频率fo相符，外圈故障特征一目了然。

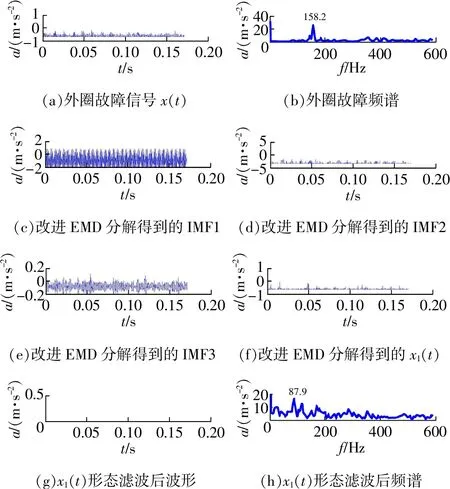
图6　外圈故障基于改进EMD和形态滤波分析结果

图7（a）为轴承内圈故障信号直接EMD分解的前4阶IMF分量频谱，图中频谱杂乱，特征信息无法呈现。图7（b）为对应IMF分量经形态滤波后再进行频谱分析的结果，可以看出谱线比滤波前有一定的改善，而且IMF1分量的滤后频谱中有故障频率成分146 Hz，但特征频率两侧的边频带不够清晰，比图5（h）中采用本文方法得到的效果要差一些。

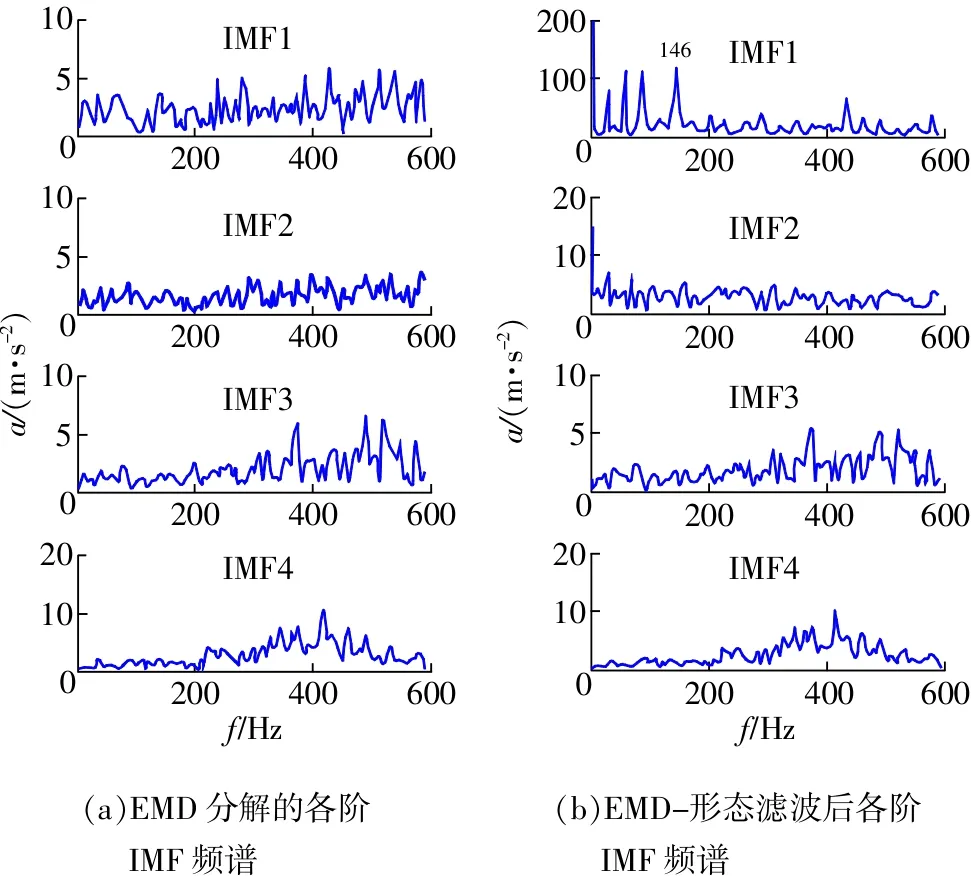
图7　内圈故障EMD及其形态滤波后频谱

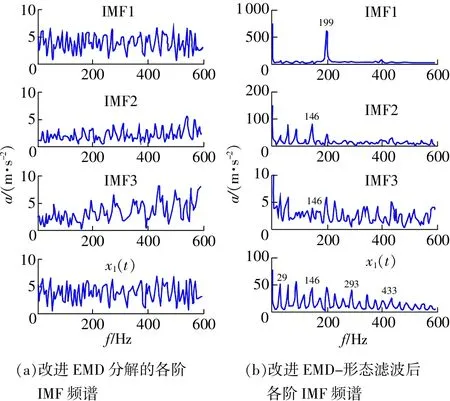
图8　内圈故障改进EMD及其形态滤波后频谱

图8（a）为轴承内圈故障信号利用改进EMD分解的前3阶IMF分量及异常事件x1（t）的频谱，图中很难分辨出故障特征频率。图8（b）为信号改进EMD后经形态滤波对应分量的频谱图，除了IMF1分量无法得到故障信息以外，其余分量均有146Hz成分，其中IMF3的特征频率能量较小，不够突出，IMF2和x1（t）信号中146 Hz非常突出，后者比前者有清晰的边频成分。对比分析可知，本文研究方法比其他几种方法更能取得满意的结果。

4　结束语

1）信号直接EMD处理由于存在模态混叠问题，导致分解质量下降，影响特征信号的提取。改进EMD方法是在原信号中加入合适的高频谐波后再进行EMD分解，使冲击性异常事件限定在高频固有模态分量中，不但改善了EMD分解效果，抑制了模态混叠现象，而且也有利于提取或消除冲击性异常事件。

2）提出基于改进EMD和形态滤波相结合的信号分析新方法。通过改进EMD来提取冲击性异常事件，然后利用形态滤波对冲击性异常事件进行处理，消除噪声干扰，从而有效提取冲击特征信息。滚动轴承故障往往具有周期性冲击特征，因此，该方法能够有效获取滚动轴承故障特征信息，实现故障诊断。

3）信号仿真和轴承故障诊断实例的结果表明，该方法能有效提高故障诊断的准确性，为滚动轴承故障特征提取提供了一种新的研究方法，具有一定的应用前景。

参考文献

[1] HUANG N E，SHEN Z，LONG S R. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceeding of Royal Society of London Series，1998（454）：903-905.

[2]杨江天，周培钰.经验模态分解和Laplace小波在柴油机齿轮系故障诊断中的应用[J].机械工程学报，2011，47（7）：109-115.

[3] HUANG N E，WU M，LONG S R. A confidence limit for the empirical mode decomposition and Hilbert spectral analysis [J]. Proceeding of Royal Society London A，2003（459）：2317-2345.

[4]赵进平.异常事件对EMD方法的影响及其解决方法研究[J].青岛海洋大学学报，2001，31（6）：805-814.

[5]刘小峰，秦树人，柏林.基于小波包的经验模态分解法的研究应用[J].中国机械工程，2007,18（10）：1201-1204.

[6] WU Z H，HUANG N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method [J]. Advances in Adaptive Data Analysis，2009，1（1）：1-41.

[7]陈略，訾艳阳，何正嘉.总体平均经验模态分解与1.5维谱方法的研究[J].西安交通大学学报，2009，43（5）：94-98.

[8]胡爱军，孙敬敬，向玲.经验模态分解中的模态混叠问题[J].振动、测试与诊断，2011，31（4）：429-434.

[9] NIKOLAOU N G，ANTONIADIS I A. Application of morphological operators as envelope extractors for impulsive-type periodic signals［J］. Mechanical Systems and Signal Processing，2003，17（6）：1147-1162.

[10]胡爱军，唐贵基，安连锁.基于数学形态学的旋转机械振动信号降噪方法[J].机械工程学报，2006，42（4）：127-130.

[11] WANG J，XU G H，ZHANG Q，et al. Application of improvedmorphological filter totheextractionof impulsive attenuation signals[J]. Mechanical Systems and Signal Processing，2009（23）：236-245.

（编辑：莫婕）

Rolling bearing fault diagnosis based on improved EMD and morphological filter

WEN Cheng，ZHOU Chuande
（College of Mechanical and Power Engineering，Chongqing University of Science and Technology，Chongqing 401331，China）

Abstract:A new technology is proposed to solve the non -stationarity in vibration signals of antifriction bearing faults in accordance with the improved empirical mode decomposition（EMD）and morphological filters. First，a high-frequency harmonic was added into the original signal and then decomposed by means of EMD to reduce the mode mixing phenomenon in traditional EMD. Next，the high-frequency harmonic was removed from the high-frequency intrinsic mode component （IMF）to obtain fault impact compositions. The fault characteristic information was extracted by spectrum analysis after morphological filter de-noising. At the same time，the above steps were simulated by signals. This method was applied to diagnose the faults in inner and outer races of antifriction bearings. The experimental results showthat the method can extract the fault characteristics and diagnose the faults of antifriction bearings.

Keywords:improved empirical mode decomposition；morphological filter；rolling bearing；fault diagnosis

作者简介：文成（1972-），男，副教授，硕士，研究方向为信号分析与处理、机电测试与故障诊断。

基金项目：国家自然科学基金项目（51205431）

收稿日期：2015-07-28；收到修改稿日期：2015-08-17

doi：10.11857/j.issn.1674-5124.2016.01.026

文献标志码：A

文章编号：1674-5124（2016）01-0121-05