温室滴灌系统支管水力性能及简化计算研究

丁法龙，王文娥，胡笑涛，徐竹涛，刘岭楠

(西北农林科技大学水利与建筑工程学院，陕西 杨凌 712100)

温室滴灌技术作为一项农艺节水新技术，不仅节水效果显著，而且可以改变温室内的小气候，使作物在较好的环境下生长，在应用实践中取得了显著成效[1]。微灌管网水力计算是微灌系统设计和校核的依据，是分析管网动态、实行优化运行的基础，但目前其设计理论及方法很不完善，大多沿用大田微溉系统的设计方法。由于温室面积、种植结构、密度等与大田差异较大，沿用其设计方法很不适宜。水力计算的任务主要是计算微灌系统管网的水头损失与压力分布，对于工程设计而言，水力计算结果的准确性直接影响到灌水均匀度和系统成本[2]。对于滴灌毛管的水力计算，国内外学者已经进行了较为充分的研究。Christiansen首先于1942年提出使用多孔系数法计算多孔管水头损失，避免使用精度高但计算繁琐的步进法。吴义伯(1992年)和Valiantzas(1998年)等人提出并修正了能量廓线方程确定滴灌毛管的沿程压力水头，使多孔管水力计算大为简化。Jain SK等人建立了毛管流量公式对滴灌毛管进行水力解析，Vallesquino等人提出连续近似(successive-approximation scheme)的方法用于毛管管路的简化计算，虽然取得了较高的计算精度，但相比于步进法，计算量并没有明显减少。近年来，随着新兴算法与计算机技术的发展，又相继出现了人工神经网络、数值模拟等方法来预测滴灌管路上的水头损失。以往对毛管的解析及简化计算，中外学者多基于管路沿线均匀泄流的假设，温室中的滴灌管铺设长度较短(一般6～10 m)，沿程压降较小，基于灌水器等量出流假定的计算结果与实际情况差异不大。但对于同为多口出流管的支管来说，由于管内流量大、管件扰流等因素的影响，其沿程的毛管出流量呈现出明显的差异，故等量出流的假设已经不适用于滴灌支管管路的水力解析，因此有必要对滴灌系统的支管进行水力性能试验研究及相关水力计算。

本研究的主要目的是分析不同毛管间距、不同支管长度、不同首部压力条件下温室滴灌支管水力性能的变化规律，基于量纲分析和实测数据建立支管水头损失及沿程压力分布形式的回归预测模型，为滴灌系统水力计算的简化提供参考。

1 材料与方法

1.1 试验装置与方案设计

试验在西北农林科技大学中国旱区节水农业研究院灌溉水力学实验厅内进行。根据普通单栋温室(60～80 m×6～8 m)滴灌系统的实际应用情况，滴灌支管采用目前国内较为多用的内径为32 mm的PE管，毛管为直径16 mm内镶圆柱迷宫流道滴灌管，单根毛管长6 m，在支管上单侧单向(沿温室跨度方向)布设，支管及毛管水平布置，滴头间距0.3 m，每根毛管含20个滴头。滴头流道宽1 mm，流道深1.5 mm，该试验前测定滴头的压力流量关系为Q=13.91H0.605(Q为滴头流量，L/h；H为滴头作用水头，MPa)。支管末端用堵头封堵，支管和毛管靠PE旁通连接件打孔连接。所有管道及管件均由陕西省杨凌秦川节水灌溉公司生产提供。

试验装置由恒压变频柜、蓄水箱、水泵、精密压力表、管式压差计以及连接好的支管单元等设备构成。水泵额定扬程为60 m；精密压力表的精度等级为0.25级，量程为0～0.25 MPa；变频装置是由宝鸡市秦川测控科技有限公司生产的QC-75变频恒压控制供水系统。试验布置见图1。

支管水力性能影响因素包括毛管间距、支管长度和首部压力，根据我国典型温室规格尺寸及作物种植结构、密度及系统运行要求设置各影响因素水平。温室作物的行距集中于30～120 cm，毛管间距s设置0.6、0.9、1.2 m 3个水平；单栋温室长度为60～100 m，支管长度L设置为20、40、60、80、100 m 5个水平；滴灌系统的常规操作压力一般为0.10 MPa，但在温室中该压力使滴灌系统对地形的适应能力被闲置，造成浪费[3]，从经济运行的角度出发，目前滴灌系统也向低压方向发展，因此首部压力h0设置为0.03、0.04、0.05、0.06、0.07、0.08、0.09、0.10 MPa 8个水平。共设置120组工况。每组试验开始时，首先打开恒压供水变频柜，设定所需压力水头。由于水泵到支管入口处有一定的水头损失，在支管首、末端安装精密压力表，首部压力表读数作为支管入口的压力值，管道运行平稳后，开始测量数据。支管上每隔5 m用压差计分段测量水头损失，在管首压力已知的条件下进而可求得支管上各个测点的实际压力值，每组试验分段测试完压差后，得到管道总的水头损失，再通过管道首、末端压力表读数之差校核压差计所得水头损失，保证误差控制在5 cm以内，否则重新测量。

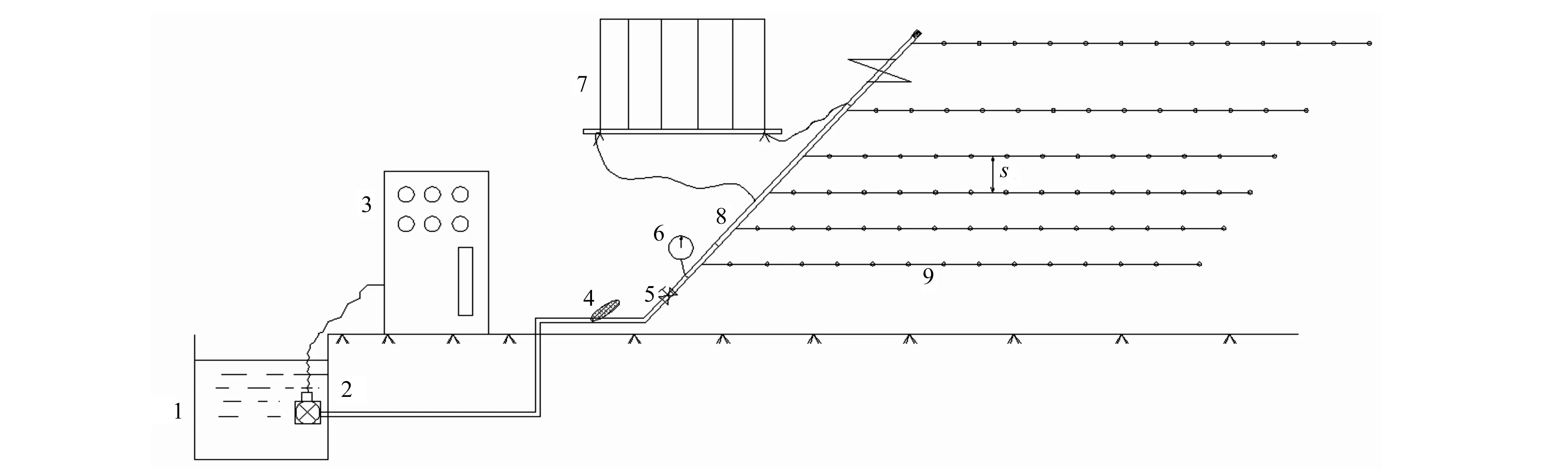
1-水箱；2-水泵；3-恒压变频柜；4-过滤器；5-球阀；6-精密压力表；7-压差计；8-支管；9-毛管图1 试验布置示意图

1.2 支管水头损失的量纲分析

支管上所测得的总水头损失包括各个无泄流支管段上的沿程水头损失和分流结点处的局部水头损失，局部水头损失主要是毛管连接件嵌入支管的部分对水流扰动产生(支毛管连接细部见图2)。由于该处水流及边壁条件较极为复杂，对产生局部水头损失的机理难以准确解析。对于多孔管，工程计算中一般先求取同径、等流量的完整管的沿程水头损失，然后分别乘上折减系数(多孔系数)和扩大系数来计算多孔管的沿程水头损失和总水头损失。实际上，相比于完整管，多孔管水头损失计算时的先折减、后扩大都是源于分流结点处水力条件的变化。结点分流导致支管中流量减小，沿程损失也相应地折减，但结点处也导致边壁条件变化从而产生局部损失，故再对多孔管沿程水头损失进行倍比扩大来估算支管总水头损失。该计算过程本质上依然是经验估算，由于多孔系数F和局部损失扩大系数K都是起因于分流结点，笔者认为在支管计算中没必要把二者分开，而且多孔系数F的现有公式都是基于多孔管沿程等量出流假定得来，支管内流量大、沿程压力变化大，即各毛管入口处压力不同，各毛管流量也不同，基于沿程均匀泄流管的水头损失计算方法对于支管的水力计算将产生较大误差。

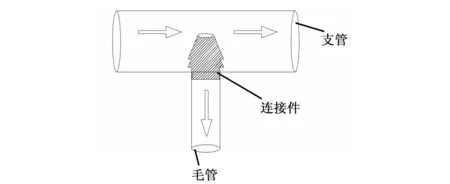
图2 支、毛管连接件细部图

因此本文采用量纲分析方法，以表征管网结构水力条件的无量纲量群为自变量，根据实测的支管总水头损失hw进行多元经验拟合。

根据支管总水头损失的构成可知：

(1)

用多孔系数法计算支管总损失时还可以写成如下形式：

(2)

式中：hw为支管总损失，m；i为支管段和连接件序号；hfi、hji分别为第i段支管上的沿程损失和第i个结点处的局部损失，m；N为管段和连接件的总数；λi为第i段上的沿程阻力系数；s为毛管间距，m；d为管径，m；υi为第i段上的支管断面平均流速，m/s；g为重力加速度，m/s2；α为局部损失系数；F多孔系数或沿程阻力系数的折减系数；λ为等流量完整管的沿程阻力系数；v为支管入口平均断面流速。

依据上式可得影响支管损失的基本变量(见表1)。以上参数中除支管入口流速υ与管道中的流量相关以外，其他量均为常数或者确定的技术参数，其中g取9.8 m/s2，ν按水温20 ℃取值为1.007×10-6m2/s。下面讨论入口流速υ的取值问题。

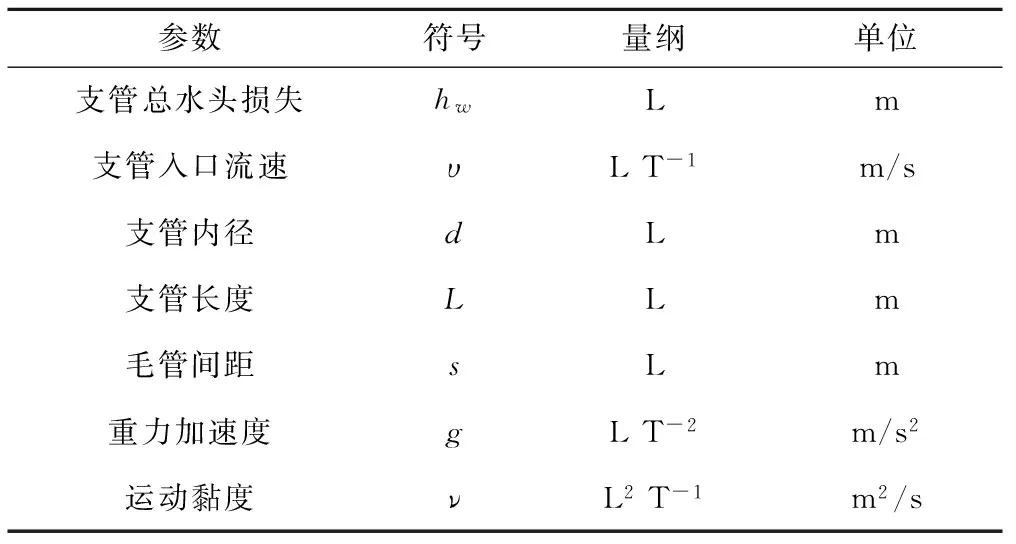
表1 影响支管水头损失的基本量

由于本试验中毛管长度是根据温室跨度布设，单根长度约6 m(包含20个滴头)，较短，同一根毛管沿程压力变化很小，滴头流量变化很小，为了简化试验过程，分析中采用每根毛管第1个滴头流量的20倍作为毛管入口流量，故毛管流量的简化公式可写成：

q毛=20×13.91h0.605

(3)

式中：q毛为毛管的入口流量，L/h；h为毛管的入口压力，MPa。

笔者选取若干典型毛管入口压力进行出流量实测，实测的毛管流量与首个滴头流量的20倍相差很小，都在1.1%以内，说明该简化计算可以较准确地表示毛管入口压力水头与流量的关系。在各个测点压力已知的条件下，各个毛管的入口压力可根据已知的测点压力由样条插值法获得。由式(3)可求出各毛管流量，进而求得支管入口流量(各毛管流量之和)及入口流速。

为方便和谐量纲公式的经验拟合，将以上基本量进行量纲的交叉运算，在保证没有变量缺失的前提下，确定了表2中所列出的一组无量纲量。

表2 影响支管水头损失的无量纲导出量

由于多孔管沿程不断泄流，管中的损失分布是非线性的，文中的支管总平均水力坡度J只是为了对支管损失hw去量纲时引入的一个中间变量；3个导出的自变量可分别反映支管结构参数及水力条件。表2中因变量J和导出量均为无量纲量，可根据试验实测数据对总平均水力坡度进行多元回归。

2 结果与讨论

2.1 试验结果分析

(1)支管长度。支管首部压力、毛管长度及间距一定时，支管越长，灌水面积越大，同时支管管首通过的流量也越大，单位长度支管的水头损失越大，灌水均匀度有可能无法保证。

图3给出了毛管间距为1.2 m，首部压力0.05 MPa，不同管长条件下的支管沿程压力分布曲线。压力分布曲线的横坐标为测压断面距支管始端的长度l与支管全长L的比值，即支管管线的相对长度，纵坐标为该点压力值与首部压力的比值，即该点的相对压力。需要说明的是，由于毛管分流及管件扰流造成的局部水头损失在接口处会表现为压力的间断跳跃，本文在绘制压力曲线时假定此处的局部损失平均分配到支管管线上，即采用了光滑、无跳跃间断点的曲线形式。由图3可知，沿程压力分布符合下降的凹形曲线趋势，即沿水流方向上单位管长的压降逐渐减小，这是因为支管沿程泄流，导致沿支管上流量逐渐减小，越靠近末端流量越小，因此水头损失也越小。在其他参数不变时，支管长度越短，支管沿程的相对压力越高，这是因为管长减小使得所连接得毛管减少，出水量随之减少，在首部压力不变的条件下使得管内压力升高，且支管内的沿程压力分布也更均匀。管长20 m时，支管总水头损失为首部压力的2.04%，而管长100 m时则升高至75.46%，且支管铺设越长，距离管首相同长度处的相对压力越低，如支管总长40 m时40 m处(管道末端)与管首的相对压力为0.898，而支管总长80 m时在40 m处(管道中点处)与管首的相对压力仅有0.57。

图3 毛管间距1.2 m首部压力0.05 MPa管长不同时的支管沿程压力分布曲线

根据滴灌设计规范，为保证所要求的灌水均匀度，灌水器流量偏差率不得大于20%，结合滴头的水力特性参数，在不考虑毛管上流量偏差和制造偏差情况下得出支管上的最大允许压力偏差为30.85%，即保证末端相对压力在69.15%(图3中虚线)以上，通过对毛管间距1.2 m时所有工况的分析，发现60 m及其以下的管长能够满足本试验所设计的所有首部压力下整个支管单元上的流量偏差要求，对于0.9 m和0.6 m的毛管间距，支管最大允许铺设管长分别为40 m和20 m，因此，在温室滴灌中，应根据灌水小区大小及常用的操作压力适当地选取支管铺设长度，以保证水力偏差在满足要求的范围内。

(2)毛管间距。作物种植的行距决定了毛管间距的大小，支管长度一定时，毛管间距越小，支管单位长度上通过的流量越大，水头损失也越大，但有可能使得支管末端的毛管作用水头太低，而无法满足作物对流量和灌水均匀度的要求。为使得试验设计水平更加全面且符合实际应用情况，在管长20 m时补充了毛管间距为0.3 m情况下水头损失的测量试验。图4给出了支管长度为20 m，典型首部压力分别为0.03、0.06、0.09 MPa条件下的支管沿程压力分布曲线。由图4可知，其他参数为定值时，毛管间距越小，支管上压力变化越显著，且毛管间距在0.6 m以上时压力分布曲线较为平缓，毛管间距0.3 m时损失急剧增大，造成其沿程压力分布极不均匀。图4中h0=0.09 MPa时，毛管间距为1.2、0.9、0.6 m的支管末端相对压力分别为0.978、0.96、0.932，而间距为0.3 m时相对压力快速降低到0.711。这是因为毛管间距越小，相同支管长度上的毛管数量增加，支管内流量及毛管接口数量的增加都会使得支管上的水头损失增大。

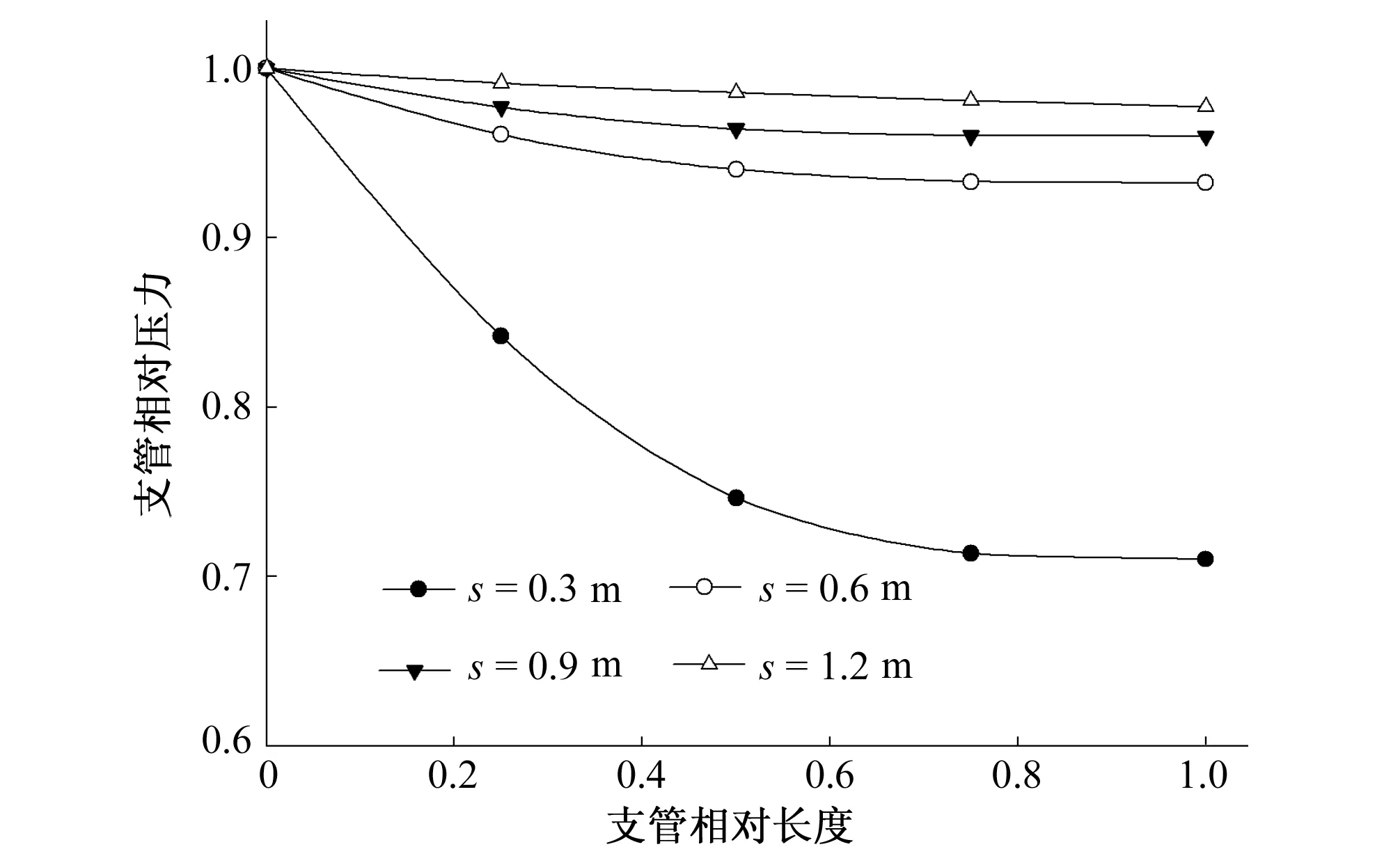
图4 管长20 m首部压力0.09 MPa毛管间距不同时的支管沿程压力分布曲线

(3)首部压力。在滴灌实际运行中，灌水器流量及一次灌水时长需要变换支管单元首部压力来调节。支管长度、毛管长度及间距一定时，支管首部压力越大，管首通过的流量越大，单位长度支管的水头损失越大。而且压力直接关系到系统的运行费用，因此是滴灌系统中很重要的技术参数。图5给出了毛管间距为1.2 m，管长60 m，不同首部压力条件下的支管沿程压力分布曲线。在其他参数不变时，首部压力越高，虽然损失值增加，但支管沿程的相对压力也越高，管内的沿程压力分布更均匀，如h0=0.03 MPa时，支管末端相对压力为0.675，h0=0.10 MPa时，末端相对压力为0.822，即首部压力升高使得压力降幅变小。

图5 管长60 m毛管间距1.2 m首部压力不同时的支管沿程压力分布曲线

2.2 支管水头损失预测模型

支管总平均水力坡度J的多元回归函数采用式(4)所示的形式，该形式相对简单且便于实现线性化：

(4)

式中：a，b，c，e为待定参数，其他符号意义同上。

对式(4)等号两端取对数运算，把原问题化为多元线性问题，然后运用MATLAB数学软件进行多元函数的线性回归，回归结果见表3,决定系数R2为92.4%。

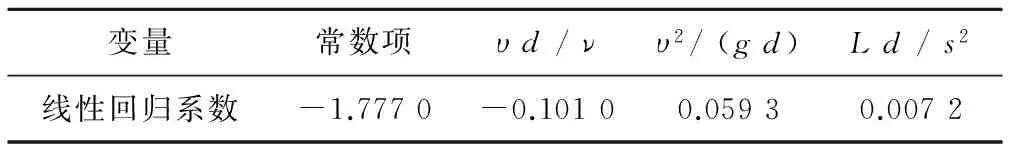
表3 支管总平均水力坡度的多元回归计算结果

由线性回归结果可得支管总平均水力坡度的回归预测模型：

(5)

将ν，g，s，d的值代入式(5)，经整理后，得到支管总水头损失的回归预测模型：

hw=0.048 5υ0.017 6L1.007 2s-0.014 4

(6)

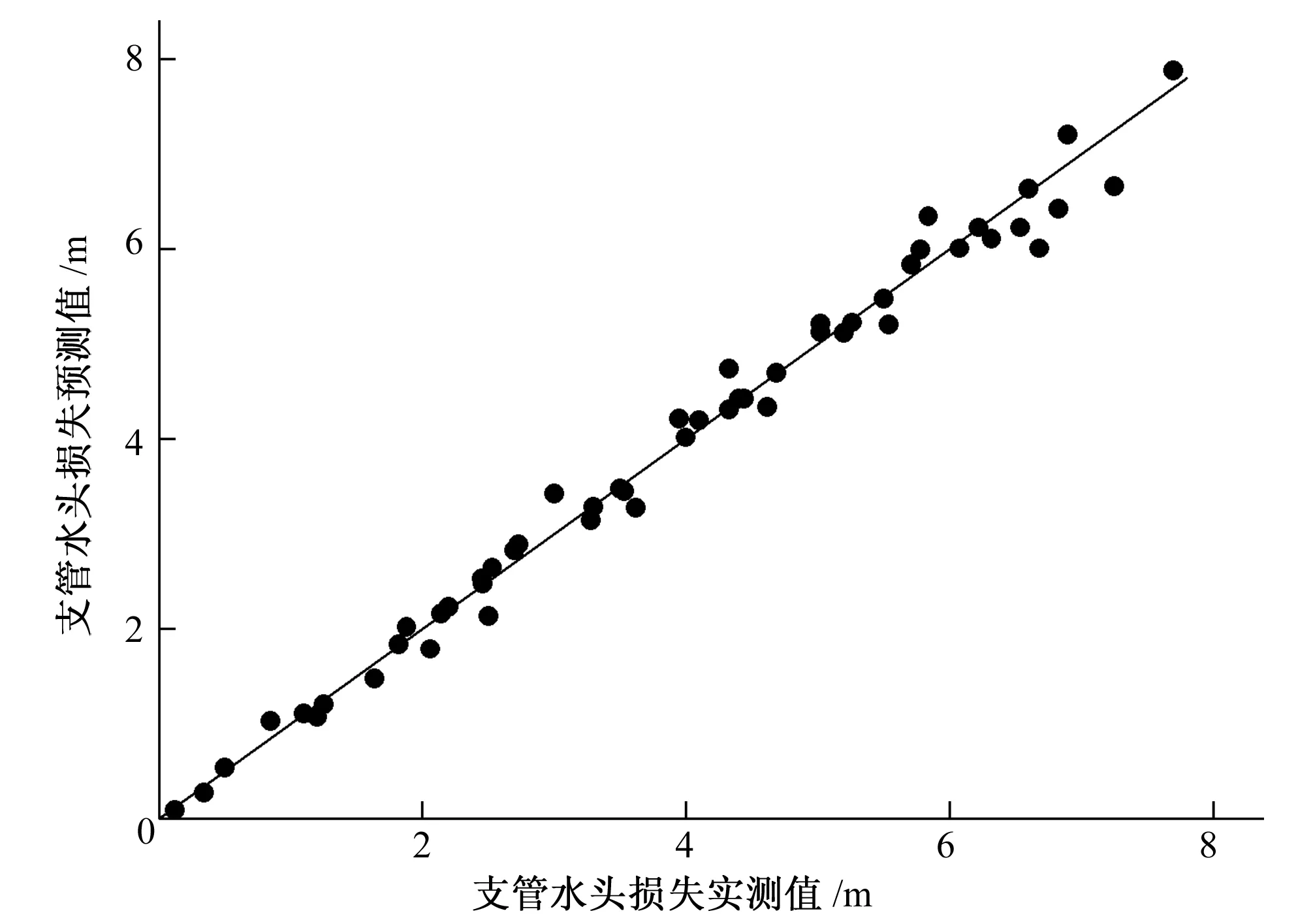
图6 支管水头损失实测值与计算值对比

图6给出了支管水头损失实测值与回归公式预测值的对照，可见实测数据集中分布于1∶1正比例直线附近，证明得到了较好的拟合结果。

2.3 支管沿程压力分布

已往学者在对滴灌毛管进行分析时，曾使用水头损失比Rx这一无量纲量来表示管路上的能量坡度线[4]：

式中：hx为x点处的压力，m；其余符号意义同前。

根据以上定义可知水头损失比Rx表示的是管路沿线水头损失的累积曲线，由于滴灌支管是沿程泄流的多孔管，单位管长上的水头损失逐渐减小，水头损失的累积速率也逐渐减小。若以管路相对坐标x为自变量，则支管上的能坡曲线是一个自变量和因变量变化范围都为0～1，且斜率逐渐减小的递增函数图像，由此可假定水头损失比分布为形如式(7)的指数型函数，其中c为待定参数：

Rx=1-(1-x)c

(7)

对试验所涉及工况进行公式(7)的经验回归，得到参数c的经验值为2.73，图7给出了4种不同典型工况下以水头损失比表示的支管能坡线实测值与回归公式预测值的对照。

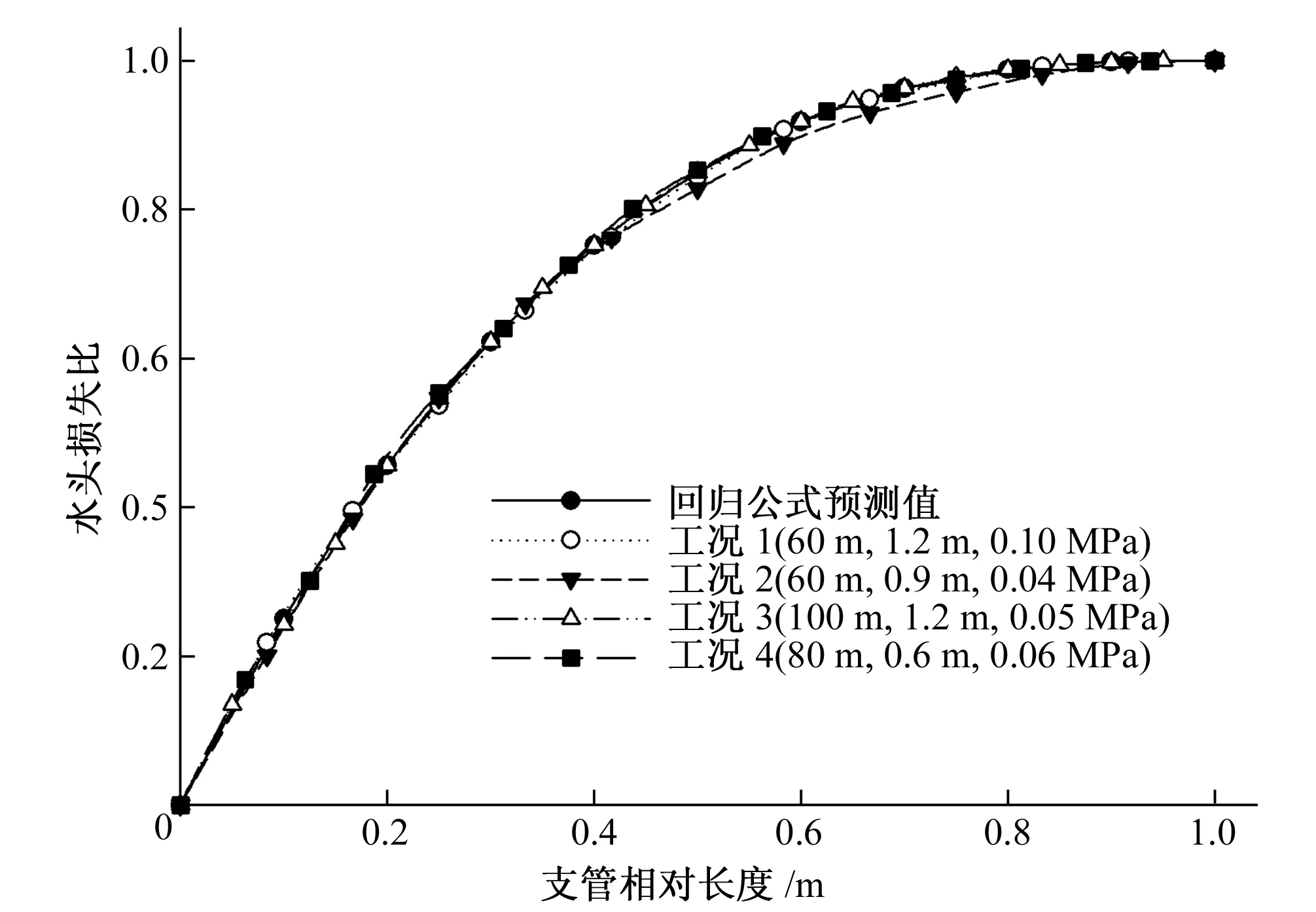
图7 典型工况下能坡线的实测值与公式预测值对照

在支管总损失及能坡曲线形式已知的条件下，支管沿程的压力分布可根据水头损失比定义并联立式(6)、(7)得到：

hx=h0-0.048 5υ0.017 6L1.007 2s-0.014 4[1-(1-x)2.73] (8)

取hx与首部压力h0的比值作为该点处的相对压力hxr，则：

hxr=1-0.048 5υ0.017 6L1.007 2s-0.014 4h-10[1-(1-x)2.73]

(9)

从图6、7可以看出，以上3种数学模型的预测值与实测数据拟合效果良好。式(5)～(9)是在本试验方案设计的条件下得出，在与试验条件类似的情况下，可由支管单元结构和水力参数直接计算得到支管损失、能量坡度及沿程压力分布形式，为温室滴灌系统支管单元的水力计算及设计、校核提供参考。

3 结 论

(1)支管上的水头损失随毛管间距的减小、支管长度的增大而增大。根据滴灌设计规范，为保证所要求的灌水均匀度，灌水器流量偏差率不得大于20%，结合滴头的水力特性参数得出支管上的最大允许压力偏差为30.85%，即保证末端相对压力在69.15%以上。通过对实测数据的分析，得到毛管间距在0.6、0.9和1.2 m条件下，满足水力偏差要求的支管最大铺设长度分别为20、40和60 m。在实际滴灌设计中，应根据灌水小区大小及常用的操作压力适当地选取支管铺设长度。对于毛管间距较小的铺设情况，可以通过合理划分轮灌组或在在支管沿线设置多个给水阀的方式来保证足够的灌水均匀度。

(2)入口压力增大在使得损失增大的同时也使得支管沿线压力分布更为均匀，如毛管间距为1.2 m，管长60 m条件下，h0=0.03 MPa时，支管末端相对压力为0.675，h0=0.10 MPa时，末端相对压力为0.822。但入口压力大小关系到系统运行费用的高低，不宜片面追求灌水均匀度来升高压力。

(3)针对目前温室滴灌支管水力计算需要推求多孔系数、估算扩大系数、计算量大等问题，运用量纲分析方法将影响支管水头损失的基本量导出为3个无量纲量υd/ν，υ2/ (gd)，和Ld/s2，通过多元回归建立支管水头损失的经验预测模型。分析了支管能坡曲线的函数形式，回归得到了支管水头损失比和沿程压力分布模型。以上3种预测模型都是由实测数据回归得到，在与试验条件类似的情况下可用于实际计算。

[1] 姚振宪,王三建.我国滴灌发展历程及建议[J].农业工程,2011,(2):54-58.

[2] 苏德荣.微灌系统压力变化对出流均匀度影响的概率分析 [J].水利学报,1991,(12):31-35.

[3] 张国祥,吴普特.滴灌系统滴头设计水头的取值依据 [J].农业工程学报,2005,21(9):20-22.

[4] 张志新.滴灌工程规划设计原理与应用[M].北京:中国水利水电出版社,2007.

[5] 谭 明,陈天胜,马卫兵,等.滴灌系统设计灌水均匀度问题的分析[J].节水灌溉,2003,(5):18,23.

[6] 蔡小超,刘焕芳,李 强,等.微灌自压软管毛管灌水均匀度的试验研究[J].节水灌溉,2005,(5):8-10.

[7] 王文元,董玉云.温室、大棚滴灌系统设计与管理中值得注意的问题[J].节水灌溉,2000,(3):15-16.

[8] Jain SK，Singh KK，Singh RP, et al. Microirrigation lateral design using lateral discharge equation [J].Journal of Irrigation and Drainage Engineering,2002,128(2):125-128.

[9] Vallesquino P, Luque-Escamilla P L. New algorithm for hydraulic calculation in irrigation laterals[J]. Irrig. Drain. Eng.,2001,27(4):254-260.