基于字典学习的机织物图像重构

毛兆华， 万贤福， 汪 军, 1b， 周 建， 卜佳仙，

陈 霞1a, 1b， 李立轻1a, 1b

(1. 东华大学 a. 纺织学院; b. 纺织面料技术教育部重点实验室, 上海 201620;

2. 江南大学 纺织服装学院, 江苏 无锡 214122)

基于字典学习的机织物图像重构

毛兆华1a， 万贤福1a， 汪 军1a, 1b， 周 建2， 卜佳仙1a，

陈 霞1a, 1b， 李立轻1a, 1b

(1. 东华大学 a. 纺织学院; b. 纺织面料技术教育部重点实验室, 上海 201620;

2. 江南大学 纺织服装学院, 江苏 无锡 214122)

首先对机织物图像进行窗口分割，将每个窗口展开成列向量，所有列向量联合组成一个矩阵；然后对该矩阵进行字典学习，得到个数最佳的字典，即基向量；最后应用该字典对待检测样本进行近似，并设计了基于信息熵的指标对原图像与近似图像之间的近似程度进行量化.重点探讨了字典模型类型和字典个数对图像重构效果的影响.结果表明，所提出的字典学习方法能够对机织物很好地近似，此外，有约束求解字典的模型对图像重构的效果优于无约束模型.

机织物； 图像重构； 字典学习； 纹理表征； 字典个数； 信息熵

(a. College of Textiles; b.Key Laboratory of Textile Science & Technology, Ministry of Education, 1. Donghua University, Shanghai 201620, China; 2. College of Textiles and Clothing, Jiangnan University, Wuxi 214122,China)

自然界中事物的纹理多种多样，纹理分析一直是计算机视觉的核心研究内容之一.对机织物图像进行重构的实质是寻找机织物的纹理信息.由于图像纹理的多样性与复杂性，目前对图像纹理的定义还不是特别精确，因此，所用的纹理分析方法也是建立在对纹理的不同理解的基础上，其大体分为4大类[1]:基于结构[2-3]、基于统计[4-5]、基于模型[6-7]和基于信号处理[8-10]，前3类都是基于空间域，最后1类是基于频率域.基于统计的方法通过定义一些统计量来对纹理结构在空间分布上的统计特征进行描述，该类方法包括灰度共生矩阵法、灰度直方图统计法，以及直接从像素灰度值中计算图像的一些直观统计量，如均值、标准差、熵等.基于结构的方法将纹理视为由许多结构基元在空间上的重复排列所形成，以结构基元为基础进行纹理描述.基于模型的方法以数学模型对产生纹理的随机过程进行建模描述，主要方法有随机场模型法、分形模型法等.基于信号处理方法则直接将纹理图像视为一维或二维的信号，以数学变换为主将纹理信息从空间域变换到频率域对纹理进行描述，主要有傅里叶变换方法、小波变换方法等.

傅里叶变换和小波变换等频域分析方法的出现为机织物图像的重构提供了有效的工具.前者采用正弦或余弦函数作为基函数对信号进行表达；后者采用满足一定条件下的小波基对信号进行表达.然而，由于傅里叶变换和小波变换皆采用固定的字典(基向量)，在对特征各异的信号进行表达时，对信号内容的适应性并不总是很理想，尤其是对高维信号的表达.近年来，使用字典学习进行信号的表达受到了广泛的关注，特别是在计算机视觉领域，与传统上使用固定的或预先定义的字典表达方法相比，通过学习所得的字典能够更好地适应信号特征，允许字典学习对输入信号进行更有效的表达.此外，目前字典学习方法主要应用于数字图像去噪[11]和人脸识别[12]等方面，很少有研究者将其用于机织物图像重构方面，因此，本文提出一种基于字典学习的机织物图像重构的方法.

1 基于字典学习的图像重构原理

在信号处理领域中，信号通常可以分解为一些基本元素或函数的线性组合来进行表达.对机织物纹理信号线性表达的基本思路是去寻找一些基元素(称为字典)，这些基元素的线性组合可以在一定的约束下对原信号进行最优的近似(重构).

1.1 字典学习

设m×n型的数据矩阵X= [x1, x2, …, xn]， xi∈Rm，i=1, 2, …,n，其中，n为样本个数，m为向量维数.在l2范数近似条件下，所要寻找的字典可以写成如下优化问题：

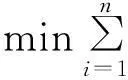
(1)

式中：D=[d1, d2, …, dk], dj∈Rm为所要学习的字典；k为字典个数；αi∈Rk为X中元素xi的系数向量.对d1, d2， …, dk约束主要是为了限制D中元素值.

显然，对式(1)进行最小化，也就意味着去寻找这样一个字典，该字典元素的线性组合能够对所有样本xi进行最小平方误差下的近似.

由于式(1)中D和α皆未知，如何构造D通常被称为字典学习问题，所得的字典称为学习字典.

1.2 算法原理

将织物图像分割为一定大小的子窗口，每个子窗口代表一个样本.在l2范数近似条件下，通过样本对式(1)进行优化求解，能对所有样本在最小平方差条件下进行最优近似表达.为了得到预期更好的学习字典，可以对式(1)施加额外的约束或构造新的目标函数，从而获得很好的表征效果.

1.2.1 无约束模型

无约束即是对字典和系数矩阵没有任何限制条件，在l2范数近似条件下，其构造模型如式(1)所示.

对式(1)进行最小化，所得的学习字典能够在最小平方误差下对所有样本进行最优近似.求解时可以将其中一个变量D或α固定，这样每一部分都可以看作一个最小二乘问题，使用交替最小化方法进行求解.

若令A= [α1, α2, …, αn]为系数矩阵，则迭代规则为

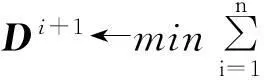
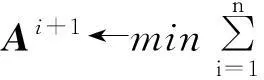
一直循环，直到‖Di+1Ai+1-DiAi‖F2<ε时停止运算，此时也就得到了学习字典D.

1.2.2 非负约束模型

基于重构误差最小建立数学模型，即

本文采用有效集(activeset)改进的非负矩阵分解算法[13]，即基于有效集方法的交替非负最小二乘算法.有效集方法是一个可行点方法，即每个迭代点都要求是可行点，每次迭代求解一个不等式约束的二次规划.该算法具有优异的收敛性能，故选取该算法来优化学习字典.

在学习阶段，本文先把机织物图像切割成一定大小的子窗口，并视每个子窗口为一个样本.接着将子窗口样本按列展成为列向量，并将所有的样本向量并列组合成为一个矩阵，并记为X.然后，对所得的矩阵实施字典学习并提取最佳个数为k的字典列作为最佳字典元素，D=[d1, d2, …, dk].

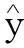
(3)

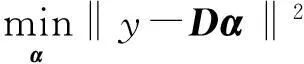
显然，若要使近似效果最佳，则有必要对所用的学习字典个数进行优选.

2 学习字典个数的优选

机织物由相互垂直的经纱和纬纱系统按一定规律交织而成，所形成的织物图像表面呈现出很强的周期性，即织物像素点间存在大量的相关性.当采用上述优化模型的算法所得的学习字典D进行表达时，通常很小的字典(字典个数k<20)就可以对机织物纹理的主体结构信息进行有效的表征，从而可以很好地近似机织物图像.

在得到机织物的学习字典之前，首先要确定字典的个数.从式(1)可以直观看出，学习字典的个数直接决定了重构误差的大小，即字典个数越多，重构误差会越小，但字典个数过多时，又会增加计算的复杂性，故本文需要选取一个适中的字典个数.

为了将学习字典对样本的近似程度进行量化，本文设计了一个称为近似指数(简记为E)的量化指标，其定义为

(4)

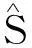
E所在的区间为0%～100%，当近似样本与原样本完全一致时，则E=100%.对于表征而言，E越大表示字典对该种织物的表征能力越强.

为了能清楚说明式(4)中所定义的量化指标的有效性，以平纹织物的样本为例，近似效果如图1所示.当k=3时，近似效果几乎达到90%，此后随着字典个数的增大，近似效果没有显著增加，故可以选定平纹织物最佳字典个数k=3.

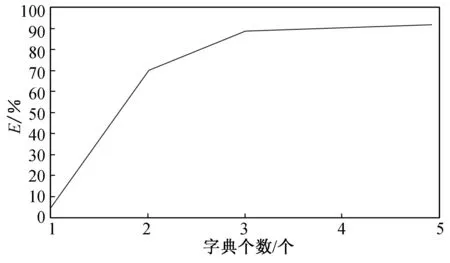
图1 平纹织物的近似指数随字典个数变化的曲线Fig.1 Approximate index curve of plain fabric with different dictionary number

3 试验结果与讨论

本文试验中所有测试图像都来自生产一线，为了方便起见，子窗口大小取32像素×32像素.按织物纹理，将织物图像分成平纹数据集和斜纹数据集，并采用式(4)提出的量化指标评价近似效果.为了验证算法的重构效果，本文选用27种不同背景纹理的织物样本进行统计，共包括平纹样本数据集60个和斜纹样本数据集48个，其中每种织物取4个样本图像进行测试，共测试平纹样本240次和斜纹样本192次.平纹织物和斜纹织物图像重构的近似指数统计如表1所示.

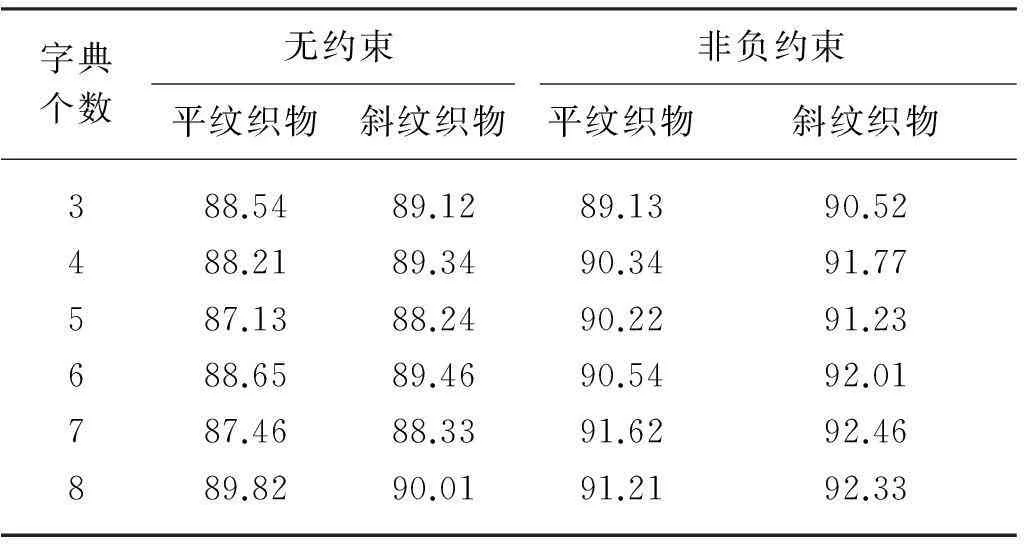
表1 平纹织物和斜纹织物图像重构的近似指数统计

由表1可以看出，当k=3时就能对平纹织物图像进行很好的近似重构，其后随字典个数的增大，近似指数并未有显著提高.如图2所示为平纹织物图像所得的3个字典元素，这3个字典很明显地包含了平纹结构的信息，故利用这些字典就可以对相应的平纹织物进行图像近似.

图2 平纹织物的学习字典(k=3)Fig.2 Learned dictionary for plain fabric (k=3)

斜纹织物的最优字典个数需要不断地尝试来选取.例如对于一些规则度很高的斜纹织物样本而言，仅需要2个字典元素就可以对机织物图像近似表达(如图3所示)，所得斜纹织物的学习字典很清晰地展示了斜纹的纹理结构.

图3 斜纹织物的学习字典(k=2)Fig.3 Learned dictionary for twill fabric (k=2)

由近似指数能明显得出基于非负约束模型的学习字典的近似效果优于无约束模型.这是因为非负约束使得字典元素都是非负，这就使得一些冗余的无用信息被剔除了，在相同的字典个数情况下，非负约束模型得到的学习字典的有用信息更多，近似效果也较好.

此外，从表1可以观察到， 有时当k较大时，相应机织物的近似指数反而会较小，即近似效果会稍微变差.这种情况大都出现在无约束模型中，其主要原因是在无约束模型中，字典个数越多时，相应得到的冗余信息也会越多，这样会使得样本与原图像之间的信息熵值比变小.非负约束模型中也会出现这种情况，但是差异很小，这可能是试验误差引起的.

为了更直观地了解机织物图像的重构效果，在不同字典个数的情况下，平纹样本和斜纹样本图像(图4所示)的重构效果，如图5所示.

(a) 平纹织物

(b) 斜纹织物

由图5可以看出，字典个数越大，织物图像的近似效果越好，不过当k=5， 7， 9， 11时近似图像相差不大，这与表1的结果趋势基本一样，故没有必要选取太大的字典个数.因为选取的字典元素过多，不仅重构效果改善不明显，而且计算量会增加，使得计算时间相应增加，从而影响织物图像重构的效率.此外，从图5还可以看出，斜纹织物图像的重构效果优于平纹织物，与表1中相应的统计结果相吻合，这是因为斜纹织物的纹理比平纹织物规整清晰.

4 结 语

本文在字典学习的基础上，提出了一种机织物图像重构的研究方法，着重探讨了字典个数对机织物图像重构效果的影响，并通过构造量化指标——近似指数来进一步确定最佳的字典元素.

试验结果表明，当k=3时，平纹织物就能得到近似效果比较好的重构图像，而斜纹织物则需各自探讨最佳字典个数.此外，在相同的学习字典个数下，非负约束模型的算法比无约束模型的近似效果好，因为非负约束只存在加法运算，所得字典的有用信息比较多，故近似效果比较好.

当然，本文利用字典学习方法对平纹样本和斜纹样本分别重构了240次和192次，考虑到样本容量和试验次数对重构结果的影响，下一步可以采集更多的样本织物来研究相应的图像重构效果，此外可将本文的近似结果进一步应用于机织物瑕疵检测的研究.

[1] TUCERYAN M, JAIN A K. The handbook of pattern recognition and computer vision [M].Singapore: World Scientific Publishing Co, 1998：207-248.

[2] 王锋,焦国太,杜烨.基于数学形态学的织物疵点检测方法 [J].测试技术学报,2007,21(6):515-518.

[3] 祝双武,郝重阳,李鹏阳,等.基于纹理结构分析的织物瑕疵检测方法 [J].计算机应用,2008,28(3):647-649.

[4] 韩立伟,徐德,王麟琨.基于统计信息的织物瑕疵自适应检测 [J].电子器件,2008，31(3)：979-983.

[5] 高晓丁,汪成龙,左贺,等.基于直方图统计的织物疵点识别算法 [J].纺织学报,2005,26(2):121-123.

[6] CAMPBELL J G,FRALEY C, MURTAGH F, et al. Linear flaw detection in woven textiles using model-based clustering [J]. Pattern Recognition Letters, 1997,18(14):1539-1548.

[7] 步红刚,黄秀宝,汪军.基于多分形特征参数的织物瑕疵检测 [J].计算机工程与应用,2007,43(36):233-237.

[8] 阮秋琦.数字图像处理学 [M].北京:电子工业出版社,2013:75.

[9] KUMAR A, PANG G K H. Defect detection in textured materials using Gabor filters [J]. IEEE Transactions on Industry Applications, 2002,38(2):425-440.

[10] DUNN D, HIGGINS W E. Optimal Gabor filters for texture segmentation [J]. IEEE Transactions on Image Processing, 1995,4(7):947-964.

[11] 解凯,张峰.基于双正交基字典学习的图像去噪方法[J].计算机应用,2012,32(4):1119-1121.

[12] 朱杰,杨万扣,唐振民.基于字典学习的核稀疏表示人脸识别方法[J].模式识别与人工智能,2012, 25(5):859-864.

Woven Fabric Image Reconstruction Based on Dictionary Learning

MAOZhao-hua1a,WANXian-fu1a,WANGJun1a, 1b,ZHOUJian2,BUJia-xian1a,

CHENXia1a, 1b,LILi-qing1a, 1b

Firstly, normal woven fabric image is partitioned into small sub-windows and vectorized into a column vector, then all the column vectors are combined into a matrix. Secondly, the matrix composed of column vectors is solved by dictionary learning, and the optimal dictionary(basis vectors)is extracted. Finally the dictionary is applied to reconstruct testing samples and the entropy-based index is calculated to qualify the proximity between original and reconstruction image. Effects of the model types and number of dictionary on image reconstruction are also investigated deeply. Experiments show that the proposed method of dictionary learning can achieve good approximation performance. In addition, learning dictionary with constraint performs better than unconstraint.

woven fabric; image reconstruction;dictionary learning; texture characterization; number of dictionary elements size; information entropy

1671-0444(2016)01-0035-05

2014 -12-05

国家自然科学基金资助项目(61379011)

毛兆华(1989—)，女，江苏南通人，硕士研究生，研究方向为机织物瑕疵自动检测.E-mail：h15006180077@163.com

汪 军(联系人)，男，教授，E-mail：junwang@dhu.edu.cn

TS 101.9

A