台阶式溢流坝消力池底板脉动压强特性研究

赵相航，解宏伟，郭 馨(青海大学水利电力学院，西宁 810016)

近几十年来，随着碾压混凝土技术的迅速发展，台阶式溢洪道因具有消能效果好，施工工期短、掺气浓度大等优点在各类中小型工程中广泛应用，同时可以大大缩减消力池长度，因此受到各国研究人员的关注，并进行了大量的研究工作[1-6]，但对台阶式溢流坝消力池内水力特性的研究较少。在台阶段与消力池之间不设反弧段时，下泄水流直接冲击消力池底板，加剧了水流的紊动混掺，其脉动压强变化具有周期性，其压强值时大时小，往复作用于消力池底板上，使消力池产生强烈的振动，当水流脉动优势频率与台阶式溢流坝自振频率接近时，可能使泄水建筑物发生共振破坏。Yasuda Y[7]通过模型试验对不同坡度溢洪道消力池内水跃的掺气浓度分布和紊动强度变化进行了分析，结果表明紊动强度极大值出现在主流附近；Meireles I[8]对1:0.75坡度的台阶式溢流坝坝后消力池底板上的时均压强沿程变化进行了研究，研究表明在试验范围内冲击点处的压强最大。但作用在消力池底板的脉动压强、峰值沿程变化及其频率特性需要进一步研究。本文结合某水库实际工程，采用物理模型试验方法，对台阶式溢流坝消力池底板脉动压强特性进行了系统研究，旨在为台阶式溢流坝消力池的优化设计提供参考。

1 模型设计

本文采用水工模型试验方法[9]，对某水库台阶式溢流坝消力池底板脉动压强特性进行了研究。该工程由溢流堰进口段、泄槽段、消力池和明渠组成。采用开敞式正槽溢洪道，溢流堰为实用堰型，台阶段与消力池直接连接，其间不设反弧段。模型根据重力相似准则，运用正态模型进行设计，选定模型长度比尺Lr=40，模型材料为有机玻璃。模型台阶段为固定坡度(θ=33.69°)，模型高度为102.75 cm，宽52.5 cm，消力池长50 cm，深10 cm，尾坎高5 cm。台阶式溢洪道共设置3种台阶高度(h=1.5，2.25，3.0 cm)，试验单宽流量为0.004 3～ 0.027 7 m3/(s·m)，流量利用设在下游的三角形薄壁堰测量，并对一些典型流况进行拍照。模型试验布置图见图1。

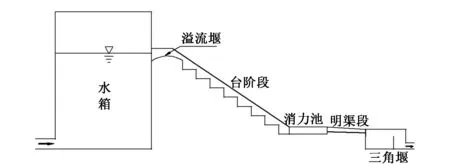
图1 模型试验布置图Fig.1 Schematic diagram of model test

为了观测台阶式溢流坝消力池底板上的脉动压强，沿消力池底板对称中心线布置一排测压孔，测点编号为测点1～测点11，如图2所示。脉动压强测量仪器选用中国水科院研制的DJ800系统进行数据采集和处理，试验采样频率为50 Hz，采样间隔为0.02 s，采样点数为4 096，采样时间为81.92 s。对采集的数据运用Matlab仿真软件进行傅里叶变换，得到台阶式溢流坝消力池底板压强脉动优势频率。

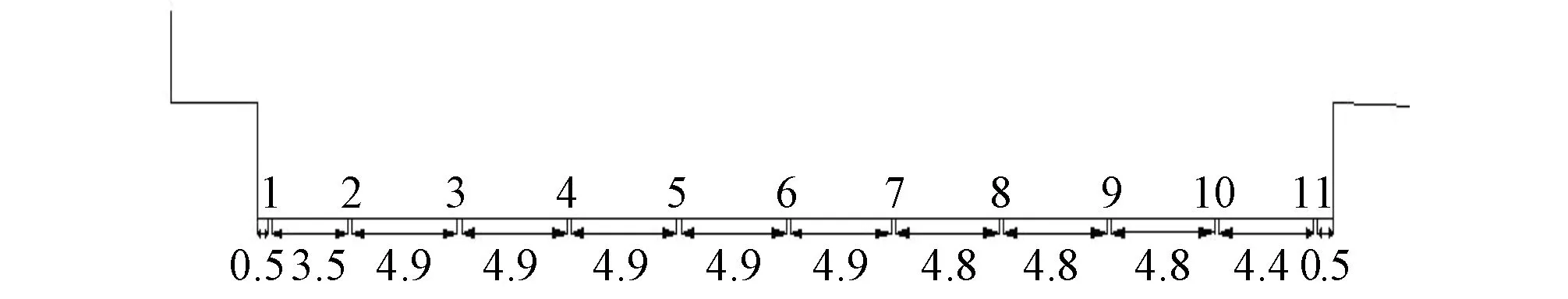
图2 模型测孔间距示意图(单位： cm)Fig.2 Schematic diagram of measuring point spacing

2 脉动压强波形图

通过采集台阶式溢流坝消力池底板脉动压强随时间的变化值，可以发现，消力池底板脉动压强随时间的变化是一个随机过程，在上游来流量恒定的情况下，水流脉动过程属于平稳各态历经的随机过程，同时发现，由于消力池内水流紊动剧烈，使脉动压强变化幅度较大。图3为试验单宽流量q=0.027 7 m3/(s·m)时消力池内不同测点脉动压强波形图，脉动压强值为模型值，下文分析中所提到的物理量也均为模型值。

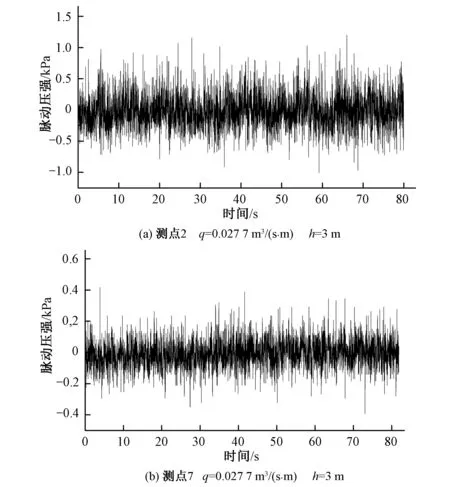
图3 脉动压强波形图Fig.3 Fluctuating pressure waveform

3 脉动压强强度分析

3.1 脉动压强强度沿程变化

我们通常把具有统计特性的脉动压强均方根称为脉动压强强度，它反映了水流的紊动强度，并表示水流脉动压强偏离其数学期望值的程度。图4为消力池底板脉动压强强度沿程变化图，图中X/L表示测点到消力池前端距离与消力池总长度的比值，下文相同。从图4中可以看出，消力池内脉动压强强度沿程变化规律较好，在跃前位置脉动压强强度较小，向下游逐渐增加，在水流冲击区出现最大值，最大值为0.274 kPa，主要原因是下泄水流冲击消力池底板，形成水跃，加剧水流的紊动和混掺，并在该位置附近形成水跃最大紊动强度区域；随后脉动压强强度沿程逐渐减小，并在减小的总趋势下有时会出现小幅起伏，最后趋于稳定，说明跃后脉动压强强度较弱，水流相对稳定，整体变化与消力池内水体紊动流态相一致。

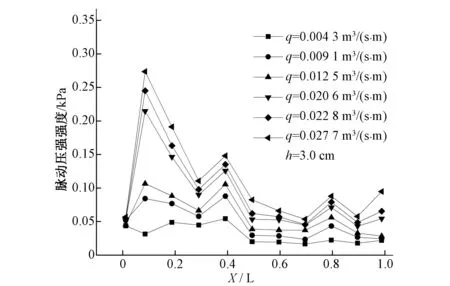
图4 消力池脉动压强强度沿程变化Fig.4 Development of fluctuating pressure intensity along the stilling basin

3.2 上游来流量对脉动压强强度的影响

对图4进一步分析发现，上游来流量是影响消力池底板脉动压强强度大小的一个重要因素，不同来流量条件下沿程变化规律一致。在单宽流量q=0.004 3 m3/(s·m)时，脉动压强强度沿程变化不明显，主要是下泄水流能量较小，对消力池底板影响不大，测点2处为水流冲击区，其脉动压强强度值为0.031 kPa，而在q=0.027 7 m3/(s·m)时变为0.274 kPa，脉动压强强度明显增加，是消力池内脉动压强强度极大区域；脉动压强强度随上游来流量的增加而增大，尤其是对水跃区的影响，分析其原因是上游来流量越大，消力池内水流紊动越剧烈，脉动压强幅值越大，从而脉动压强强度增加。

3.3 台阶高度对脉动压强强度的影响

本文还研究了台阶高度对消力池底板脉动压强强度的影响，如图5所示。从图中可以看出，脉动压强强度在不同台阶高度时沿程变化规律基本一致，均在水流冲击处(测点2)出现最大值，其脉动压强强度随台阶高度的降低而增大。在q=0.022 8 m3/(s·m)时，改变台阶高度，测点2处脉动压强强度依次增加13.31%、9.46%，主要原因是台阶式溢洪道对下泄水流产生阻碍作用，使水流发生掺气和碰撞，台阶高度越高，水流受到的阻力作用越强，水流掺气效果越明显，到达坝址处的紊动强度相对较低，进而消力池底板受到的惯性力较弱，紊乱程度随之减小，脉动压强强度也减小；在消力池内其他位置，改变台阶高度，脉动压强强度有所浮动，变化规律不显著，消力池末端脉动压强强度变化不到7%，受台阶高度影响较小。

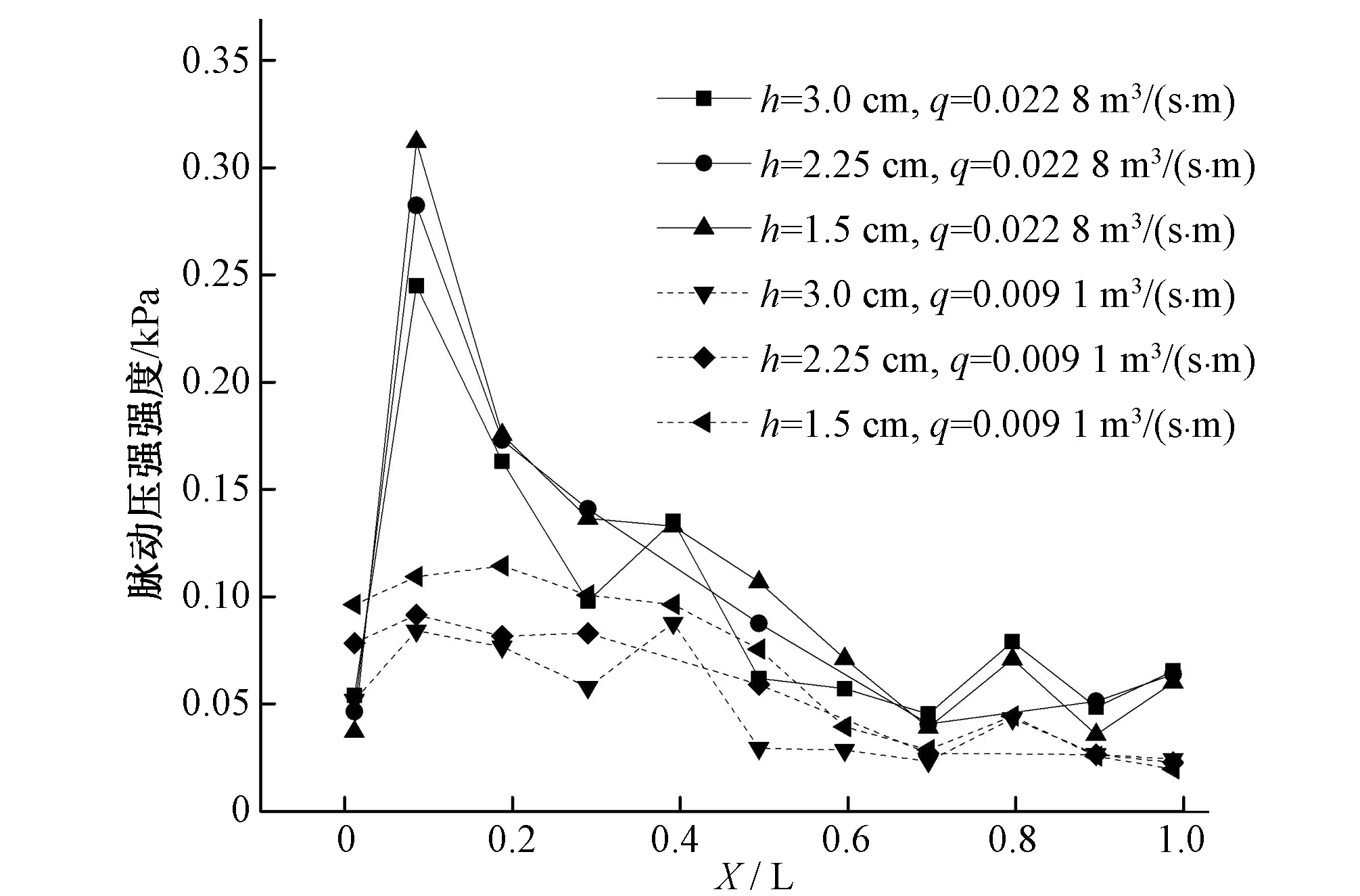
图5 不同台阶高度消力池脉动压强强度沿程变化Fig.5 Development of fluctuating pressure intensity along the stilling basin for different steps height

4 脉动压强峰值分析

4.1 脉动压强峰值沿程变化

通过提取消力池底板各测点量测时段内的脉动压强最大值和最小值，对脉动压强峰值沿程变化规律进行了分析，如图6所示。从图中可以看出，脉动压强最大值先沿程逐渐增加，在测点2处达到最大值，最大值为1.198 kPa，随后沿程逐渐减小，并逐渐趋于稳定；脉动压强最小值沿程变化与最大值变化恰好相反，脉动压强最小值先沿程逐渐减小，在测点2处出现最小值，最小值为-1.009 kPa，随后沿程逐渐增加，并逐渐趋于稳定。可见脉动压强幅值(即最大值和最小值的绝对值)越大，水跃区水流紊动越剧烈，消力池底板受水流的影响就越大，从而对底板稳定性造成的危害也越大，在实际工程中应引起注意。

4.2 上游来流量对脉动压强峰值的影响

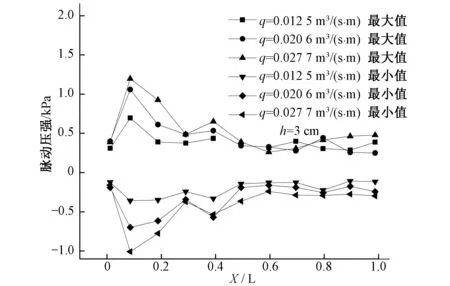
图6 消力池脉动压强峰值沿程变化Fig.6 Development of fluctuating pressure peak value along the stilling basin

通过图6研究上游来流量对脉动压强峰值的影响发现，流量对水流冲击区脉动压强幅值影响最为明显，当单宽流量q=0.012 5 m3/(s·m)时，脉动压强最大值为0.696 kPa，最小值为-0.359 kPa，脉动压强变化幅度为1.055 kPa，而q=0.027 7 m3/(s·m)时，脉动压强最大值为1.198kPa，最小值为-1.009 kPa，脉动压强变化幅度为2.207 kPa，说明随着上游来流量的增加，水流紊动加剧，脉动压强幅值增大，振动幅度随之加强。

4.3 台阶高度对脉动压强峰值的影响

台阶高度改变了溢洪道的水流性质，但是否会影响消力池内水流脉动，本文还分析不同台阶高度时消力池底板脉动压强峰值沿程分布。研究发现，脉动压强幅值在不同台阶高度时沿程变化规律一致，水流冲击区(测点2)脉动压强幅值基本上随台阶高度的降低而增大。改变台阶高度，脉动压强峰值依次增加7.75%、3.63%，增加幅度不大；而其他位置受台阶高度的影响不明显，消力池末端脉动压强峰值变化相对值不到10%，受台阶高度影响较小。图7为单宽流量q=0.022 8 m3/(s·m)时不同台阶高度脉动压强峰值变化图。

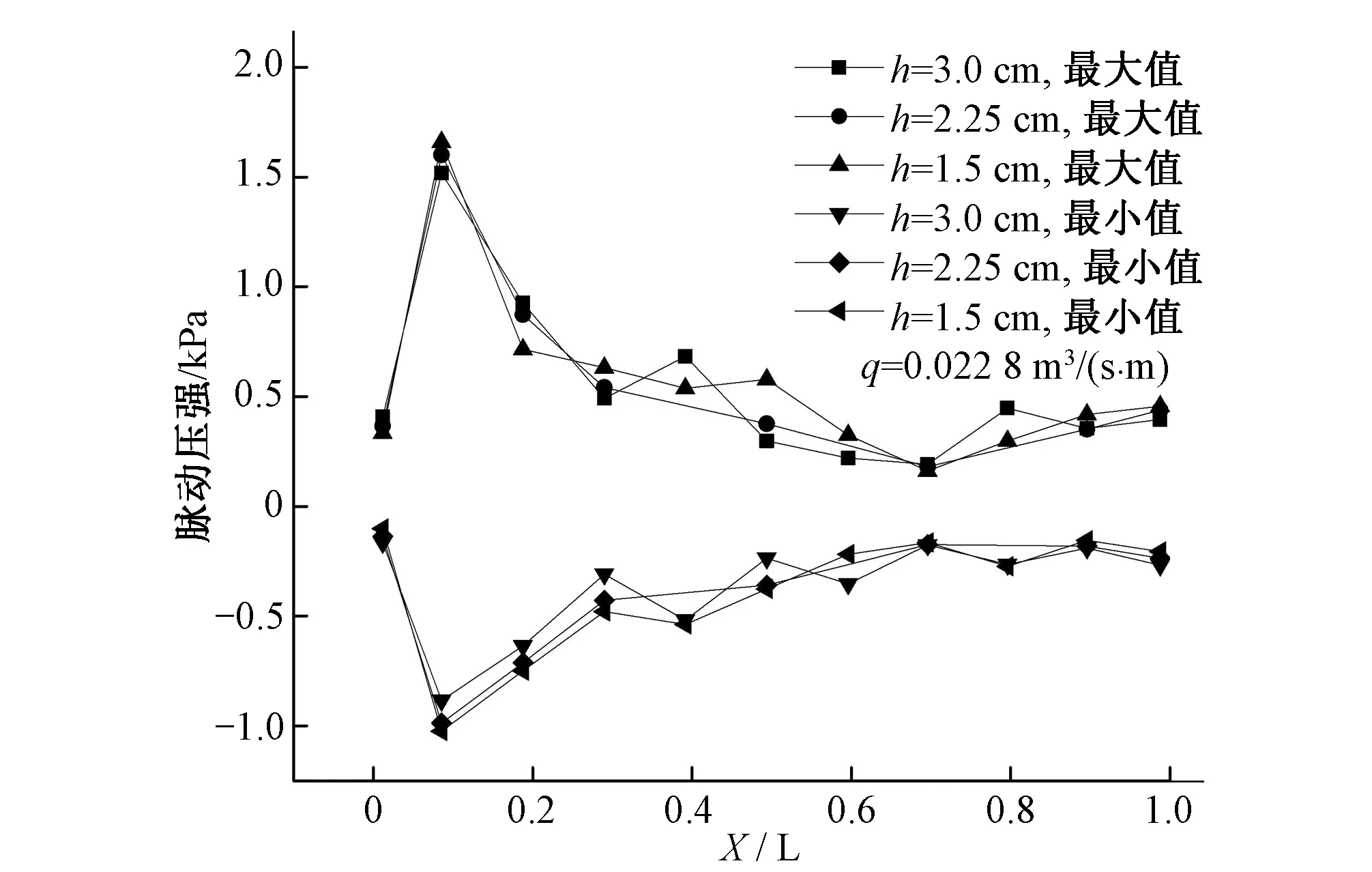
图7 不同台阶高度消力池脉动压强峰值沿程变化Fig.7 Development of fluctuating pressure peak value along the stilling basin for different steps height

5 脉动压强频率分析

通过分析可知，当上游来流量一定时，消力池内脉动压强变化是一个平稳各态历经的随机的过程。功率谱密度表示不同频率结构分量组成脉动压强的平均能量值，通过频谱分析，可以得到频谱密度最大时对应的优势频率，是水流脉动压强能量集中的代表频率，当水流优势频率与消力池自振频率接近时，将产生共振现象，使泄水建筑物发生破坏。

通过对消力池底板功率谱密度分析可知，消力池底板各测点压强脉动均属于低频振动，其水流脉动优势频率为0.01～4 Hz，水跃区脉动压强优势频率相对较大，但远远小于台阶式溢流坝和消力池的自振频率，故消力池底板产生共振破坏的可能性不大。

6 脉动压强概率密度分析

为了解台阶式溢流坝消力池内水流脉动压强随机信号的正态性，对消力池底板各测点脉动压强概率密度分布进行了研究。图8为不同单宽流量时测点2处的脉动压强概率密度分布图。由图8可知，消力池底板压强脉动概率密度不是标准的正态分布，而是偏态分布，在实际工程应用中，我们可以看成正态分布[10]进行分析。同时发现，随着流量的减小，概率密度分布曲线由矮胖型向瘦高型发展，说明脉动压强变化幅度逐渐降低。

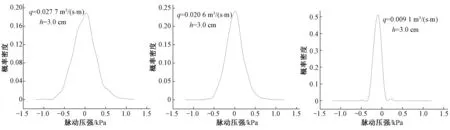
图8 脉动压强密度分布Fig.8 Probability density distributions of fluctuating pressure

7 结 语

随着台阶式溢洪道在中小型工程中的广泛应用，坝址处消力池稳定性机理的研究显得尤为重要。本文研究了台阶段与消力池之间不设反弧段时消力池内脉动压强特性。试验结果表明，消力池内水跃稳定且掺气充分，水流脉动过程属于平稳各态历经的随机过程；测点2处为水流冲击区，水流紊动剧烈，脉动压强较大，其最大值可达1.198 kPa，幅值变化也较大，对消力池底板影响显著，是其最不利点，应加强防护；随着下泄流量的增加，消力池内脉动压强增大；水跃区脉动压强随着台阶高度的降低而增大；消力池脉动优势频率为0.01～4 Hz，属低频振动，其概率密度分布属于偏态分布，不会对泄水建筑物产生共振破坏。研究成果对于台阶式溢流坝消力池的优化设计具有参考价值。

□

[1] 艾克明．台阶式泄槽溢洪道的水力特性和设计应用[J]．水力发电学报，1998,(4)，86-95．

[2] Gonzalez C A，Chanson H．Turbulence and cavity recirculation in air-water skimming flows on a stepped spillway[J]．Journal Hydraulic Research，2008，46(1)：65-72．

[3] Kiyoumars R，Samira A，Farzin S，etc．Modeling energy dissipation over stepped spillways using machine learning approaches[J]．Journal of Hydrology，2014,508：254-265．

[4] 杨吉健，刘韩生，张为法．台阶式溢洪道滑掠流时均压强影响因素分析[J]．长江科学院院报，2015，32(8)：57-60．

[5] 李布雳．台阶式溢流坝上压强特性的试验研究[D]．西安：西安理工大学，2005．

[6] 岳生娟，张法星，曲景学，等．某水库溢洪道泄洪消能的试验研究[J]．中国农村水利水电，2014，(10)：120-122．

[7] Yasuda Y，Takahashi M，Kobayashi J，et al． The effect of aerated inflow on characteristics of hydraulic jump in a sloping channel[J]．Journal of Hydraulic engineering，2002，46：601-605．

[8] Meireles I，Matos J，Falco de Melo J．PressureHead and Residual Energy in Skimming Flow on Steeply Sloping Steeped Spillways[C]∥ In：IAHR，31thCongress．Korea：Seoul，2005：2 654-2 662．

[9] SL155-2012，水工(常规)模型试验规程[S]．

[10] 郑阿漫．掺气分流墩台阶式溢洪道水力特性的研究[D]．西安：西安理工大学，2001．