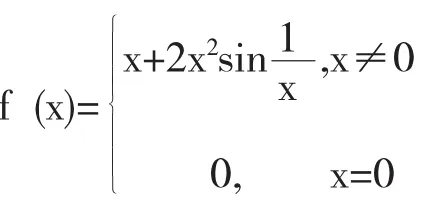函数的单调性与函数的导数之间的关系及反例
2016-03-22景慧丽杨宝珍
景慧丽,屈 娜,杨宝珍
(火箭军工程大学 理学院,陕西 西安 710025)
函数的单调性与函数的导数之间的关系及反例
景慧丽,屈娜,杨宝珍
(火箭军工程大学理学院,陕西西安710025)
摘要:利用函数的导数的正负来判断函数的单调性是导数的重要应用之一.文中把函数的单调性、函数在一区间内的导数的正负及函数在一点的导数的正负三者之间的关系进行了梳理,并给出相应的反例加以说明.
关键词:单调性;导数;反例
在微分学中,导数的重要应用之一是用来判断函数的单调性,即用函数在一个区间内的导数的正负来判断函数在该区间上的单调性,判定定理[1]是:设函数y=f(x)在[a,b]上连续,在(a,b)内可导.
(1)如果在(a,b)内f'(x)≥0,且等号仅在有限多个点处成立,那么函数y=f(x)在[a,b]上单调增加;
(2)如果在(a,b)内f'(x)≤0,且等号仅在有限多个点处成立,那么函数y=f(x)在[a,b]上单调减少.
当然,如果把判定定理中的闭区间换成其他区间(如果是无穷区间,要求在其任一子区间上满足定理的条件),那么结论依然成立.
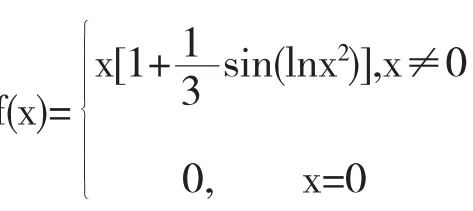
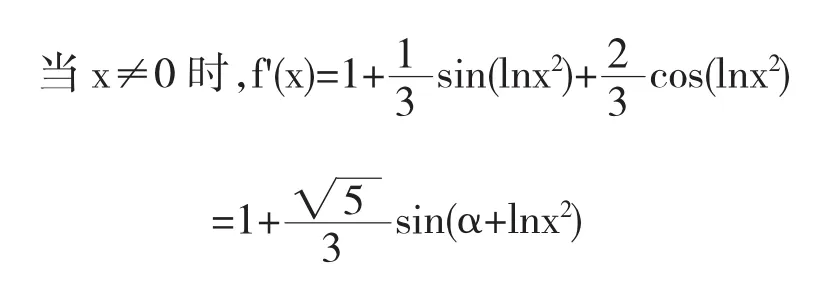
所以,当x≠0时,f'(x)>0.因此,函数f(x)在(-∞, 0)内是单调增加的,故当x1<0时,有f(x1) 一般地,如果已知一个函数在一个区间上单调增加(单调减少),是不能得到其导函数一定大于零(小于零)的.但是如果已知函数y=f(x)在区间I上是可导的,即f'(x)存在,且y=f(x)在区间I上单调增加(单调减少),那么在区间I上一定有f'(x)≥0(f'(x) ≤0)成立. 当k→∞时,显然有xk1→0,xk2→0,因此在点x=0的任何邻域内,f'(x)的取值有正有负,从而f(x) 在x=0的任何邻域内都不单调. 由此可知,函数的单调性、函数的导数的正负及函数在一点的导数的正负三者之间的关系是:如果在区间I上f'(x)≥0(f'(x)≤0),且等号仅在有限多个点处成立,则函数y=f(x)在区间I上一定单调增加(减少);反之,如果函数y=f(x)在区间I上单调增加(减少),则在区间I上未必有f'(x)≥0(f'(x)≤0)成立.另外,不能用函数y=f(x)在点x=x0处的导数f'(x0)的正负来判断函数y=f(x)在点x=x0的邻域内的单调性. 总之,用函数的导数的正负来判断函数的单调性这个看似简单的问题,学生也经常理解有偏差,通过上述总结尤其是反例的说明,可以帮助学员加深对这三个概念之间关系的理解.在《高等数学》课程的教学中教员要恰当地利用反例进行辅助教学,因为反例是反驳与纠正错误的一种有效方法[4],而且在数学的发展过程中,反例所占的重要地位同等与证明,正如美国数学家B.R.盖尔鲍姆和J.M.H.奥姆斯特德所说:“冒着过于简单化的风险,我们可以说(撇开定义、陈述以及艰苦的工作不谈)数学由两大类——证明和反例组成,而数学发现也是朝着这两个目标——提出证明和构造反例”[5]. 参考文献: 〔1〕同济大学数学系.高等数学(上)[M].第七版.北京:高等教育出版社,2007.145. 〔2〕陈汝栋.数学分析中的问题、方法与实践[M].第一版.北京:国防工业出版社,2012.20. 〔3〕马知恩,王绵森.高等数学疑难问题选讲[M].第一版.北京:高等教育出版社,2014.96. 〔4〕李春.反例在泛函分析教学中的作用[J].西南师范大学学报,2012,37(6):230-232. 〔5〕盖尔鲍姆,奥姆斯特德.分析中的反例[M].第一版.上海:上海科学出版社,1980.4. 基金项目:火箭军工程大学2015年度教育教学立项课题(EPGC2015008) 收稿日期:2015年9月19日 中图分类号:O174 文献标识码:A 文章编号:1673-260X(2016)02-0004-02