基于AIC法则和极大似然法的系统辨识分析探讨

刘海

（江西服装学院商贸分院　计算机教研室,江西　南昌　330201）



基于AIC法则和极大似然法的系统辨识分析探讨

刘海

（江西服装学院商贸分院计算机教研室,江西南昌330201）

摘要：系统辨识在当今社会中获得了广泛的应用，本文运用参数辨识方法对带有白噪声的系统进行辨识，分析研究关于系统辨识的原理和辨识过程.并设计M序列作为系统的输入与干扰信号，运用AIC法则对系统的阶次进行辨识，然后用极大似然法则对系统参数采取辨识并对结果进行了分析讨论.

关键词：AIC法则；极大似然法；系统辨识

前言

在当今社会中系统辨识被广泛的应用，可以说，只要进行实验数据确定数学模型和估计参数的场合，都需要用到辨识技术.而系统辨识的基本思想是根据系统运行或者是试验测得的数据，并按照给定的“系统等价准则”从一群候选数学模型集合里，确定一个与系统特性等价的数学模型.也就是说只要是系统的输入输出来确定描述系统行为的数学模型，是系统辨识研究的对象.在进行系统分析的一个重要方面是根据输入时间函数与系统的特性来确定输出信号，系统辨识主要有模型阶次辨识与参数辨识两种.今后，随着社会的发展，人类将更加深入地研究大范围复杂工程的应用，涉及的系统辨识会更多，包括非线性系统辨识，高维时变系统的辨识，多变量开环或闭环系统的系统辨识，整体和多级辨识以及辨识的可分离性理论等方面.本文将运用参数辨识方法对带有白噪声的系统进行辨识，白噪声在工程上人为是不可产生的，实际工程上，通常用M序列来代替白噪声输入信号.本文用AIC法则来判定系统的阶次，应用确定阶的Akaike信息准则确定系统模型的阶，根据确定系统模型阶的算法阐述程序编制思路；辨识出模型阶之后，选择极大似然算法对系统进行参数辨识，并且列表与真值和辨识算法计算结果的比较和分析.

1　系统辨识的基本步骤

在系统辨识中，系统辨识主要是根据系统的输入输出时间函数来确定描述系统行为的数学模型，所以在系统辨识的基本步骤中，首先是先验知识，先验知识主要包括系统运动规律、数据和其他方面的已存在的知识.其作用是对选择的模型结构、设计实验与决定辨识方法等都非常重要的.并且用在不同目的的模型中都表现出很大的差别.其次是建模，建模的目的对于确定模型的结构和辨识方法也有重要意义.然后是辨识，辨识是从实验数据中提取有关系统信息的过程，设计实验的目标之一是要使所得到的数据能包含系统更多的信息.主要包括输入信号设计，采样区间设计，预采样滤波器设计等.结构辨识也就是选择模型类中的数学模型M的具体表达形式.除线性系统的结构可通过输入输出数据进行辨识外，一般的模型结构主要通过先验知识获得.系统辨识的基本步骤，具体流程如图1所示.

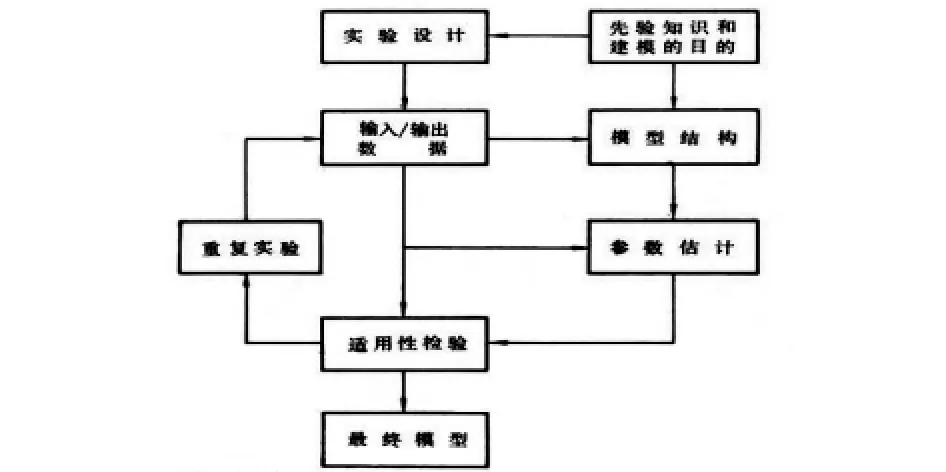
图1系统辨识的具体流程

2　辨识输入信号M序列发生器的设计

m序列是一种线性反馈的移位寄存器产生的周期很长的也是最常见的伪随机序列，也是最长线性反馈移存器，简称m序列,如图2.

图2 M序列的产生原理图

从图2序列的产生原理图所示，伪随机序列是由反馈移位寄存器产生，并分成了两类，包括线性反馈移位寄存器与非线性反馈移位寄存器.而周期最长的二进制数字序列也被叫做最大长度线性反馈移位寄存器，是由线性反馈移位寄存器产生的.图2则是一个一般线性反馈移存器的组成，图中一级移存器的状态用xi表示，xi=0或1，i=（1-4）.m序列的设计是数字电路在通信里非常常用的一种形式，其硬件设计组成有五片74HCl64串连构成，反馈信号则是由异或门MC40送出，需要注意的是钟振荡器不能由非门构成的RC多谐振荡器组成，原因是频率特别低，我们用计数器分频后实现(此处省略关于具体的硬件电路设计).

m序列作为一种最常用的伪随机码，在实际电路里M序列是由移位寄存器产生的，而本文是通过在MATLAB中用软件来实现的.通过编写一个M函数来实现要求的实际硬件电路.通过仿真可得M序列的图形如图3所示.

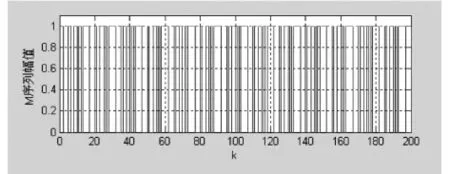
图3 M序列

3　利用AIC准则对系统的阶数的辨识

AIC信息准则是20世纪70年代日本学者赤池提出的，基于信息度量的信息准则及利用信息准则判定模型阶次的方法.AIC信息准则的定义为l1:MC(m)=-21ogL(0lz)+2M(16)上式中的logL(0lY)=logL(0IYi)为模型参数极大i=l似然估计的对数似然函数,它是各观测对数似然函数之和,为独立的模型参数个数.采用的是模型阶次判定准则，使得随机变量的真正概率分布相对于它的估计的概率分布的熵为最大，也就是使观测数据z所估计的随机变量的y的概率分布g (y)与其真正的概率分布的f(y)之间的拟合度B（f,g）为最大.

B(f,g)为信息熵,由于具有真正概率分布的f（y）的随机变量y的熵是一定的，所以式（3-2）第二项为常数，而第一项可写成

可见，要使J（g）最大，也就是要求式（3.2-3）最大，因此必须对EyIng[y/θ(z)]做出估计，利用极大似然法，经过推导，可以得

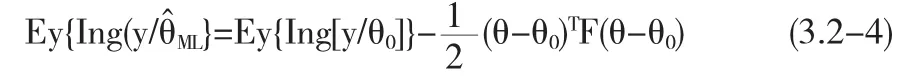
式中θ0-为真实参数；F-Fisher信息矩阵.

根据极大似然估计值的渐近性及正态随机变量和随机变量之间的关系，式（3-3）第二项渐近的具有自由度为r 的x2分布.并可得到

从上而得到，采用最小AIC方法判定模型阶数，可以归结为在不同的模型阶次下，先利用极大似然法估计出相应阶次模型下的各个参数，然后再考虑到独立参数数目下，求出在该模型阶次下的AIC值.于是，具有最小AIC值的模型阶次就是应确定的模型阶次.设干扰信号为白噪声系统模型一般表达式为：

a(z-1)y(k)=b(z-1)u(k)+ε(k)（3.3-13）

式中：a(z-1)=1-1.8z-1-1.3z-2+0.4z-3b(z-1)=1.1z-1+0.288z-2

开始任意取一组于模型相对应的阶数，由已知的输入，输出根据极大适然法就可以求相应的系数赞N，并且计算此时AIC的值，在取一组模型的任意阶数值，重复以上过程，通过比较得到AIC取得最小值时候，就是该模型所辨识的最优阶数.

通过对源程序的仿真可得到AIC值，其最小的值对应的阶次就是系统要辨别的阶次，可得na=3，nb=2可见与给点题目的阶次相同.

4　基于递推极大似然法的模型参数辨识

极大似然法由高斯提出，并由费希尔(R．A．Fisher)发展，是现代辨识的参数估计方法之一.从本质上讲是一类概率性贝叶斯估计方法，是一种应用比较广泛的常用估计方法，这种估计方法用于动态系统辨识，可以获得良好的估计

?效果.极大似然法需要构造一个以测量数据和未知参数有关的似然函数，并通过极大化这个函数获得模型的参数辨识.由上可知，极大似然法将参数估计问题归结为似然函数值为最大时候的最优化问题，所以极大似然函数法进行参数估计时候，必须掌握可观测变量y的联合概率密度分布，也就是合理确定相应的似然函数.通过仿真可辨识得到系统的参数

a1=1.813, a2=-1.1989, a3=-0.421

b1=1.098, b2=0.289

可见辨识的参数与实际值还是存在一定的误差，一方面可能数据的长度取得还不够长，实验证明数据的长度越长，得到的值越准确，所以要求获取的数据尽可能长些，另一方面可能存在一些因客观原因而存在的一些误差.

5　结论

系统辨识的过程分为几个阶段，开始是对系统的阶次进行辨识，并在阶次已知的前提下再对对系统的参数进行辨识的过程.AIC法则得到了广泛的应用，已经解决了许多系统的阶次问题，在本设计中准确的辨识出了系统的阶数，并且在得到系统阶数的前提下，利用极大似然法对系统参数进行了辨识，基本上与给出的参数相同.但是该方法也存在一些问题，按此方法估计出来的模型阶次不是渐近一致的，并且只适用于低阶系统，对于高阶系统会引起较大的误差，并且AIC估计的模型的阶数偏高，为此Kashyap和Schwar利用贝叶斯方法提出了BIC准则，可以看做是对它的改进.

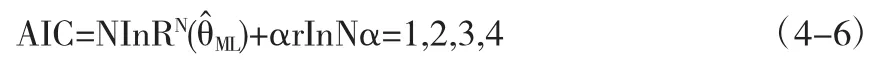
其中α可以看做是对高阶的惩罚，αInN=2时候，也就就变成了AIC准则了.

参考文献：

〔1〕黄添强，吴铁浩，袁秀娟，等.利用模式噪声聚类分析的视频非同源篡改检测[J].计算机科学与探索，2011，5（10）：914-920.

〔2〕齐晓慧，田庆民，董海瑞.基于Matlab系统辨识工具箱的系统建模[J].兵工自动化，2006，25（10）：88-90.

〔3〕张新国，马义德，李守亮，等.非线性电路：基础分析与设计[M].北京：高等教育出版社，2011.

〔4〕张聚.基于MATLAB的控制系统仿真及应用[M].北京：电子工业出版社，2012.

〔5〕刘娣，许有熊林健.基于MATLAB的“系统辨识”课程实验教学改革[J].中国电力教育，2013（1）：139-140.

收稿日期：2015年10月19日

中图分类号：TP273

文献标识码：A

文章编号：1673-260X（2016）02-0014-02