包含反应阶数变化的分形煤焦颗粒燃烧模型的建立与实验验证

刘雨廷，何榕

（清华大学热能工程系，热科学与动力工程教育部重点实验室，北京 100084）



包含反应阶数变化的分形煤焦颗粒燃烧模型的建立与实验验证

刘雨廷，何榕

（清华大学热能工程系，热科学与动力工程教育部重点实验室，北京 100084）

摘要：为了深入研究煤焦燃烧的机理并提高对煤焦燃烧过程的预测精度，建立了一个综合的煤焦燃烧模型。该模型考虑了煤焦颗粒孔隙内二次反应与扩散的耦合作用、煤焦燃烧反应阶数的变化和反应过程中CO/CO2比例等问题。使用热天平（TGA）对11种煤焦的燃烧特性进行分析，测得各种煤焦的表观活化能与指前因子，以确定模型中的待定参数。在沉降炉（DTF）中对这11种煤焦做燃烧实验，用TGA基于灰分守恒测得DTF炉管出口处的煤焦样品的转化率。运用建立的模型模拟这些煤焦的燃烧过程，预测的转化率与实验结果有较好的吻合度，相比传统的本征动力学模型，该模型预测的精度有了较大提高，证明了该模型能适用于从褐煤到无烟煤的较广煤焦范围。研究还发现，煤焦燃烧的表观反应阶数在燃烧过程中不断减小并最终趋于稳定。

关键词：煤焦燃烧；模型；模拟；沉降炉；实验验证；表观反应阶数；分形

2015-06-15收到初稿，2015-07-07收到修改稿。

联系人：何榕。第一作者：刘雨廷（1988—），男，博士研究生。

Received date: 2015-06-15.

引 言

在我国，煤是一种储量相对丰富、价格相对便宜的化石燃料。随着石油资源的日益枯竭，煤的价值与地位越发突显，如何高效地利用煤炭资源成为我国经济发展不可回避的问题。目前，对煤最主要的利用方式是直接燃烧[1]以获得热能，以火力发电为代表。

煤的燃烧大致可分为热解与煤焦燃烧两个过程。已有的研究[2-5]表明，煤燃烧发热量的80%以上来源于煤焦燃烧，且煤焦燃烧所需时间比热解要长几个量级。因此，煤的燃烧特性主要由煤焦的燃烧特性决定。所以，建立精确的煤焦燃烧模型，对于煤的高效利用，以及燃煤设备的设计与运行，都有着极为重要的意义。

煤焦是典型的多孔介质，其孔隙结构极为复杂，而且具有分形特性[6-8]。煤焦的燃烧反应不只在煤焦的外表面进行，而更多的是通过气体扩散进入孔隙内部，在孔隙的内表面进行，煤焦的孔隙结构对煤焦的燃烧特性有着重要的影响[9-15]。因此，精确的煤焦燃烧模型必须考虑煤焦孔隙结构对煤焦燃烧反应的影响。

研究者们已针对煤焦燃烧模型进行了大量的研究[1-3,16-19]，建立了许多不同的煤焦燃烧模型。其中包含了煤焦孔隙结构影响的模型之中，经典的本征动力学模型[3,17-18]应用最为广泛，而He等[2]建立的具有分形孔隙特性的煤焦燃烧模型则是通过理论推导得到的。该两种模型都认为不同煤焦的本征活化能相同，而煤焦燃烧反应速率由于煤焦孔隙结构的不同而存在很大的差异。前者[3,17-18]通过引入弯曲因子表征煤焦孔隙结构的复杂性，弯曲因子越大，煤焦孔隙结构越复杂。但弯曲因子并无严格的物理定义，且无法通过独立的实验测量或计算得到。而后者[2]则采用孔隙率、比表面积、分形维数[8]3个参数表征煤焦孔隙结构的复杂性，并与颗粒粒径这一参数共同表征煤焦的结构特性。与前者相比，后者的优点在于其计算精度更高，能更好地反映煤焦的结构参数对煤焦燃烧特性的影响，且孔隙率、比表面积、分形维数定义明确，易于独立的实验测量，用于表征煤焦孔隙的复杂程度较之弯曲因子更为合理。但是，无论本征动力学模型[3,17-18]还是He等[2]建立的煤焦燃烧模型，都假设煤焦燃烧反应的阶数恒定为1，这与实际情况不符[20-21]，难免会给计算带来误差。而且He等[2]所建立的模型中的待定参数是通过试算法得到的，方法不太严密，而且用于对比的煤焦燃烧实验数目也很有限。

本文在He等[2]所建立的煤焦燃烧模型的基础上，引入表观反应阶数的变化规律[21]和燃烧产物中CO/CO2的比例的定量描述[21-22]，并用更加严格的方法确定其模型中的待定参数，从而建立了一个可靠的煤焦燃烧模型。该模型考虑了煤焦孔隙内复杂的扩散与反应耦合的过程，不仅能预测瞬时的煤焦燃烧速率，可以方便地嵌入到一些商用计算流体力学软件（如Fluent）中，还能获得煤焦燃烧过程中更多的细节，便于对煤焦燃烧机理进行研究。使用热天平（TGA）分别对11种煤焦的燃烧特性进行研究[23]，并测得它们的表观活化能与指前因子，用来确定模型中的待定参数。在沉降炉（DTF）中对这11种煤焦进行燃烧实验[23]，用TGA测得这些煤焦在DTF炉管出口处的转化率。运用本文中所建立的模型，从最基本的流动传热传质方程出发，对这些煤焦的燃烧过程进行模拟并与实验结果对比，以验证模型的可靠性。计算的结果还与采用本征动力学模型[3,17-18]的计算结果进行比较。最后，对煤焦燃烧过程中一些关键量的变化规律进行分析。

1 模型的建立

本文所建立的分形煤焦燃烧模型主要包括3个部分：煤焦燃烧瞬时速率表达式、煤焦燃烧的表观反应阶数和燃烧产物中的CO/CO2比例。这些内容均是比较复杂的问题，但在此之前已经对它们做了大量的研究工作。

1.1 煤焦燃烧瞬时速率表达式

He等[2]通过理论推导的方法建立了煤焦燃烧速率的表达式。煤焦颗粒的示意图如图1所示，rp为煤焦颗粒的半径。假设燃烧过程中煤焦内部达到稳定状态，煤焦颗粒结构各向同性且均匀。

在r处，单位时间内扩散的氧气量为

图1 煤焦颗粒示意图Fig.1 Schematic diagram of a char particle

其中，De为氧气的等效扩散系数，c为r处氧气的浓度。

在r～ r+ d r微元体内，单位时间内消耗的煤焦可表示为

其中，ρa是煤焦的表观密度，Sg是煤焦的比表面积，ki为本征反应常数，其表达式为

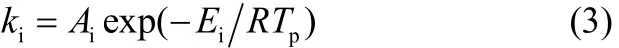
稳定状态下，微元体内所消耗的氧气量等于净扩散进入该微元体内的氧气量，故有

化简得

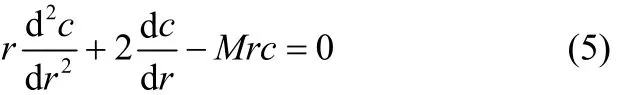
已知氧气浓度的边界条件为

其中，cs为煤焦外表面氧气浓度。

根据边界条件式（6），求解微分方程式（5），可得煤焦内部氧气浓度的分布

因此，煤焦的总反应速率可表述为

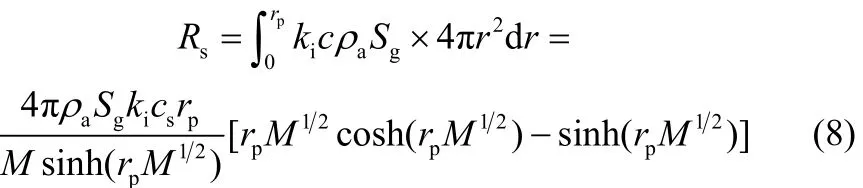
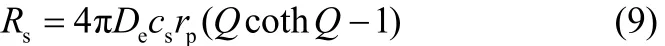
煤焦燃烧的表观反应常数ka可定义为

其中，m为煤焦颗粒质量。将Q的定义代入可得

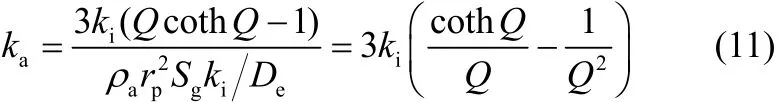
现引入模数f

式中，z为比例系数，M0为氧气分子摩尔质量，Tp为煤焦颗粒的温度，(Tp/ M0)1/2项是为体现温度对扩散系数的影响。则有

为方便分析与处理，引入新的模数c，将煤焦孔隙的所有结构参数整合到一起，其定义式为

其中，ρi为煤焦的真密度。因此，煤焦燃烧的瞬时速率表达式为

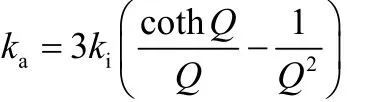
其中

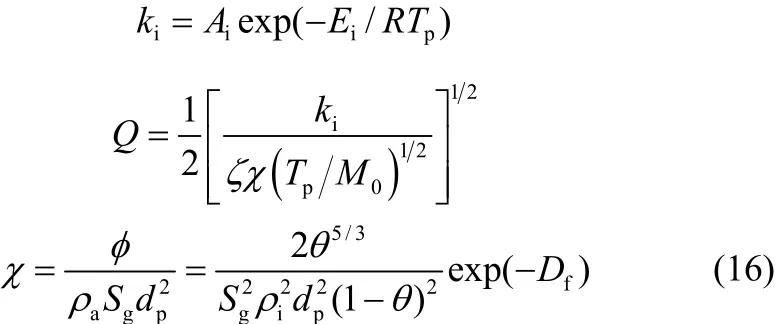
式中，Ai、Ei和z为待定参数，由实验确定。

He等[2]进一步研究表明，模数c的值越大，煤焦孔隙结构对气体扩散的阻力越小，该种煤焦就越好烧。

1.2 煤焦燃烧的表观反应阶数

目前，包括本征动力学模型在内，绝大多数煤焦燃烧模型都将煤焦燃烧的表观反应阶数取为1或其他常数，以简化计算，但这与实际情况并不相符[20-21]，难免会给计算带来误差。也有很多学者对煤焦燃烧反应的阶数进行了大量实验研究，但他们大多只给出了在特定反应条件下、对特定煤焦的反应阶数值，并没有给出一个通用的规律来[21]。这也是前面大多数模型将反应阶数取为常数的原因。

Liu等[21]采用数值模拟的方法对这一问题进行研究，归纳出了一个能够描述不同煤焦、在不同条件下的反应阶数的表达式，并与实验结果进行对比，取得了较好的效果。要介绍Liu等[21]的结果，先要对一个分形孔隙模型进行介绍。

Liang等[26]采用随机漫步算法生成了一种分形孔隙模型，它可以用来模拟真实的煤焦颗粒。图2是这种孔隙模型的示意图，可以看出它与真实的煤焦在外形上很相近。He等[8]基于对煤焦的压汞实验，定义了一种煤焦的分形维数

其中，Sa是煤焦的累积表面积，rpore是煤焦孔隙的半径。分形维数表征了煤焦孔隙结构的复杂程度，对孔内的气体扩散影响很大，是描述煤焦孔隙结构的一个重要参数。根据压汞实验的原理，Liang等[26]也给出了该种数值煤焦颗粒分形维数的计算方法。

Liu等[21]采用图2所示的分形孔隙模型模拟煤焦燃烧。在他们的模拟中，化学反应（包括碳与O2、碳与CO2及CO与O2的反应）是用简单碰撞理论描述的，煤焦孔内的气体扩散则是用分形孔隙内的气体扩散定律[24]来描述。这里并不需要对煤焦的整个燃烧过程进行模拟，而只需要得到在某一个具体条件下煤焦总的反应速率，也就是说，只需要计算出一个极短时间内整个煤焦颗粒中消耗的碳分子总数。假设两个反应温度相同、浓度相差一个小量的工况的反应阶数近似相等，通过模拟得到这两个工况下的反应速率值，便可以很容易地求得该条件下的反应阶数了。一共计算了600组工况，得到了300组有效的数据。通过对这些数据的归纳分析，得到了煤焦燃烧表观反应阶数的表达式

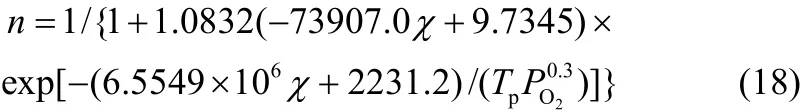
其中，χ是模数，其定义与式（16）中的χ相同，代表了孔隙结构对表观反应阶数的影响；Tp是煤焦颗粒的温度，K；PO2是颗粒表面O2的分压，atm。

Liu等[21]进一步证明了模数χ是煤焦颗粒孔隙扩散阻力的度量，χ越大，对应的孔隙扩散阻力越小。他们还给出了χ的临界值为1.3171×10-4，当煤焦颗粒的χ值大于此临界值时，孔隙扩散对煤焦燃烧速率的影响可以忽略不计。

1.3 煤焦燃烧产物中的CO/CO2比例

燃烧产物中的CO/CO2比例是影响煤焦燃烧的重要因素之一。同样质量的煤焦氧化生成CO2所释放的热量是生成CO所释放热量的3.5倍[22-23]，由于生成不同产物所释放的热量存在巨大差异，会给煤焦颗粒温度的计算带来上百度的误差。

He等[22]基于煤焦燃烧活化能高斯分布假设，并结合气体分子运动论的相关内容，对O2分子与碳分子碰撞结果进行了分类，使用概率论的相关方法计算出生成各种产物及不发生反应的概率，进而得到碳与O2反应的一次CO/CO2比例

其中，x1(ε)和x2(ε)是中间函数，具体形式见文献[22]，f(ε)是O2分子平动能的麦克斯维分布函数。之所以称它是一次CO/CO2比例，是因为它并不包括煤焦颗粒孔隙内的气体扩散与二次反应的作用，这用实验方法是很难得到的。

Liu等[21]将式(19)运用到煤焦燃烧的模拟中，通过使用图2中的数值煤焦颗粒模型，引入煤焦颗粒孔隙内的扩散与化学反应等因素，得到煤焦颗粒燃烧的表观CO/CO2比例

其中，Tp是煤焦颗粒的温度，K；PO2是颗粒表面O2的分压，atm。这与Tognotti等[27]的实验结果非常接近。

2 实 验

使用热天平（TGA）分别对11种煤焦的燃烧特性进行研究[23]，测得它们的表观活化能与指前因子，用来确定模型中的待定参数。在沉降炉（DTF）中对这11种煤焦进行燃烧实验[23]，用TGA测得这些煤焦在DTF炉管出口处的转化率。运用本文中所建立的模型对这些煤焦的燃烧过程进行模拟并与实验结果对比，以验证模型的可靠性。

2.1 实验材料

表1和表2分别为这11种煤焦对应的原煤的工业分析和元素分析结果。这些煤中既有高挥发分的烟煤，也有不太好烧的无烟煤与褐煤。将这些原煤在沉降炉中、1200℃高温、N2气氛下进行热解，以制得后面实验用的煤焦样品。热解时气体的流量为0.5 m3·h-1，气体平均流速为0.33 m·s-1，给粉速率为1 g·h-1。所得煤焦样品中残余挥发分含量很低，对后面煤焦燃烧影响很小。

要对这些煤焦的燃烧过程进行模拟，需要测量这些煤焦样品的平均粒径与孔隙参数。对于平均粒径的测量，使用的是Mastersizer 2000激光粒径分析仪，它的量程是0.02～2000 μm，测量误差在1%以内，重复测量的误差小于0.5%。对于其他孔隙参数的测量，使用的是Autoscan 33压汞仪，其操作压力范围是0～232 MPa，能测量的最小孔径是3.23 nm，非线性度为满量程的±0.05%。测得的这11种煤焦的平均粒径与孔隙参数列于表3中，其中分形维数的定义为式(17)。

表1 原煤的工业分析结果（空干基）Table 1 Proximate analyses of parent coals (dry air basis)

表2 原煤的元素分析结果（干燥基）Table 2 Ultimate analyses of parent coals (dry basis)

HV 　71.39 　4.78 　1.56 　9.81 　0.46

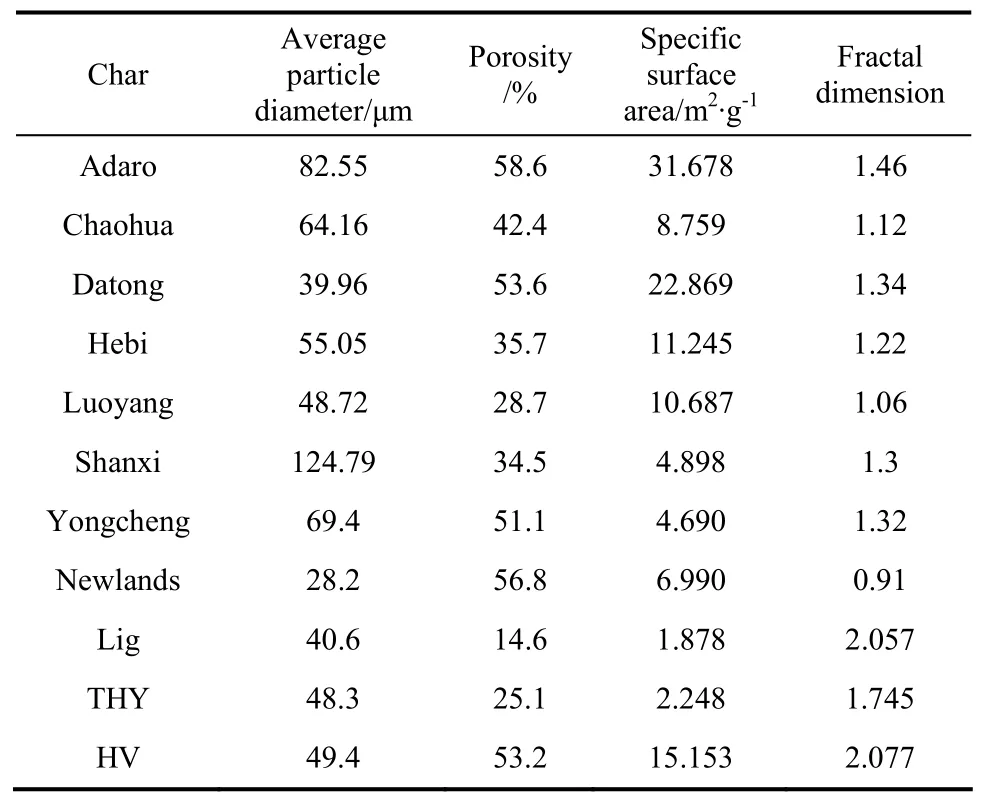
表3 煤焦样品的平均粒径与孔隙参数Table 3 Average particle diameters and pore structure parameters of chars

2.2 热重分析（TGA）实验

将煤焦样品分散均匀地置于热天平上，样品上面所通气体为空气，热重采用程序升温，温度与时间呈线性关系。由于实验过程中加热速率很慢，可以保证煤焦颗粒温度与气流温度近似相等。各种煤焦实验时温度与时间的关系如表4所示，其中，t为时间，s；T为气体和煤焦颗粒的温度，K。

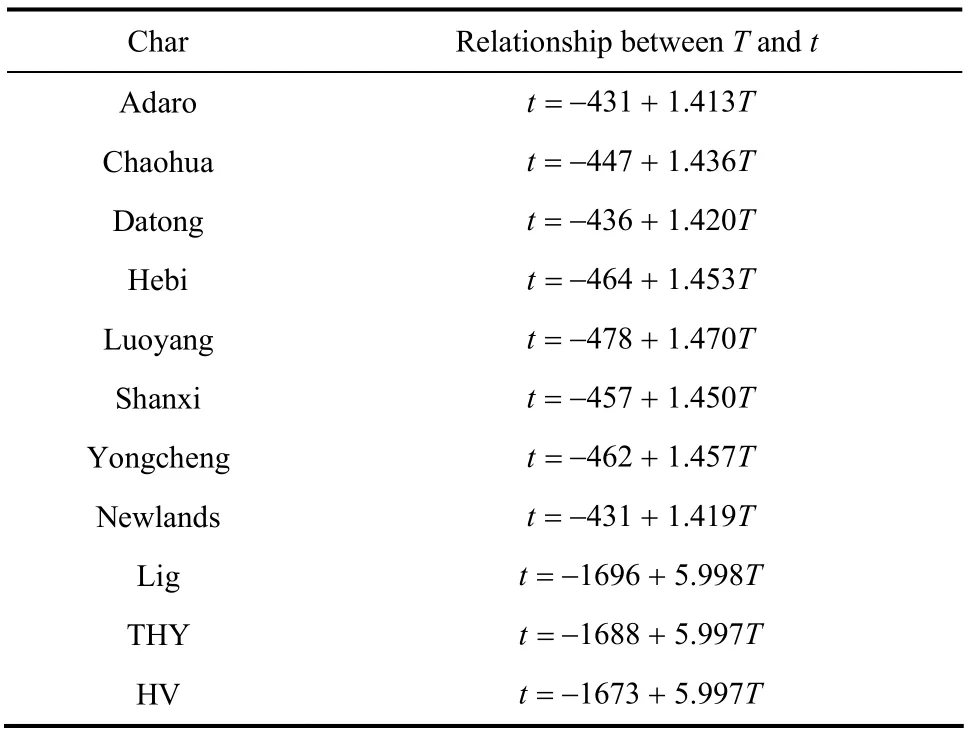
表4 TGA实验升温曲线函数Table 4 Heating curve function in TGA experiments

由于煤焦颗粒燃烧过程中粒径和孔隙结构是不断变化的[3]，只有得到与煤焦燃烧前的粒径和孔隙参数（表3中所列）相对应的燃烧动力学参数，才能确定本文所建立模型中的待定参数（Ai，Ei和）的值。于是，在处理TGA数据时，仅取煤焦转化率在0～20%之间的数据进行分析。在该段数据中，煤焦的转化率最多只有20%，用文献[3,28]中的经验公式估算得到此时的粒径与孔隙参数变化相对初始值不超过5%，因此，颗粒的粒径与孔隙参数变化均不明显，可以近似将用此段数据得到的表观动力学参数与表3中的粒径和孔隙参数对应起来。

具体求解煤焦燃烧表观动力学参数（表观活化能Ea和指前因子Aa）的方法见文献[23,29]。这里只将通过最后迭代求解的结果列于表5中。

表5 TGA实验得到的煤焦燃烧表观动力学参数Table 5 Apparent kinetic parameters of char combustion obtained in TGA experiments

2.3 沉降炉（DTF）燃烧实验

实验所用沉降炉系统的结构如图3所示。沉降炉使用电加热，炉管的内径为50 mm，炉管高为750 mm，煤焦颗粒注入炉管的位置距离炉管进口200 mm，煤焦取样点设置在炉管出口处。

图3 沉降炉结构示意图Fig.3 Schematic diagram of drop tube furnace

各种煤焦的燃烧实验条件是相同的，即沉降炉壁温为1000℃，炉内所通气体为空气，流量为0.5 m3·h-1，气体平均流速为0.33 m·s-1，煤焦颗粒的给粉速率为1 g·h-1，煤焦颗粒在沉降炉内的平均停留时间约为1.67 s。煤焦的给粉速率足够小，以保证燃烧过程中煤焦颗粒之间互不影响。

沉降炉炉管出口处所取的煤焦样品的转化率由式（21）计算

其中，X为煤焦的转化率，ash0为反应前煤焦颗粒的灰分含量，ash为燃烧后煤焦颗粒的灰分含量。ash0和ash的值均由TGA实验测得，结果列于表6中。

表6 煤焦在沉降炉中燃烧的最终转化率Table 6 Final conversions of chars in DTF experiments

3 分析与讨论

3.1 模型参数的确定

1.1节中经理论推导得到了煤焦颗粒燃烧的表观反应常数ka的表达式（16），其中包括待定的模型参数Ai，Ei和z。同时，表观反应常数ka还可以由式（22）计算

其中，Ea为表观活化能，Aa为对应的指前因子。这样式（16）与式（22）对相同煤焦、在相同温度下便可建立起一个等式关系

表5中给出了用TGA测得的11种煤焦的表观活化能Ea和指前因子Aa的值，表3又给出了式（23）等号左边项计算所需的煤焦粒径值与孔隙参数值，则对11种煤焦分取800 K、1000 K、1200 K、1400K、1600 K和1800 K这6个温度，便可得到66个等式，运用最小二乘法拟合，让这66个等式的误差最小，这时的Ai，Ei和z值即为所求。计算得到它们的值分别为

为了更直观地显示拟合精度，现将温度为800 K和1000 K时的拟合结果与实验结果的对比分别作于图4和图5中。图中实线为由式（16）结合式（24）中的参数值所作，为拟合结果；图中的点则为式（22）结合表5中的表观动力学参数计算得到，为实验结果，点与横坐标c的对应关系可以由对应煤焦颗粒的孔隙参数与粒径计算得出。可以看出拟合的效果还是不错的。

这样，式（16）、式（18）、式（20）以及式（24）中的参数值一起，构成了本文所构建的分形煤焦燃烧模型。该模型中，模数c是所有孔隙参数与粒径的组合，表征了孔隙扩散对煤焦燃烧影响[2]，c的值越大，孔隙的扩散阻力就越小，对煤焦燃烧速率的影响也就越小。当c的值大于1.3171×10-4时，可以认为煤焦孔隙扩散的影响可以忽略不计[21]。

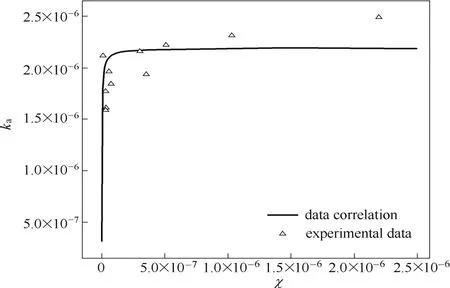
图4 800 K时拟合结果与实验结果的比较Fig.4 Comparison of data correlation results with experimental results at 800 K temperature

图5 1000 K时拟合结果与实验结果的比较Fig.5 Comparison of data correlation results with experimental results at 1000 K temperature

3.2 沉降炉燃烧实验的模拟方法

运用本文所建立的煤焦燃烧模型对2.3节中介绍的沉降炉燃烧实验进行模拟，并将预测的煤焦最终转化率与表6中的实验结果进行比较，以验证模型的可靠性。同时，再采用本征动力学模型[3,17-18]对这些实验进行模拟，也与本文模型模拟的结果进行比较。

沉降炉中的流动是一个典型的气固两相流，可以用Euler-Lagrange方法对此进行模拟。作为连续相的空气用基本的Navier-Stokes方程进行描述，而作为离散相的煤焦颗粒通过跟踪已确定的流场中颗粒的运动轨迹来描述。在计算当中，煤焦颗粒与空气流场不断交换质量、动量与能量。由于煤焦颗粒的尺寸较小，颗粒之间的相互作用以及颗粒对流场的影响被忽略。

计算时使用的三维网格如图6所示，一共有22万个节点。空气从气体入口（gas inlet）进入炉管，煤焦颗粒从离进口200 mm的颗粒源（particle source）注入，忽略了颗粒注射器对流场的影响。模拟中使用的具体方程见文献[2]，这里只对煤焦燃烧模型嵌入部分进行介绍。

图6 沉降炉的三维网格Fig.6 3D-grid of drop tube furnace

煤焦颗粒燃烧速率方程为

其中，ka为煤焦燃烧的表观反应常数，由1.1节中建立的燃烧速率模型[式（16）]来描述，m为煤焦颗粒的质量，Sg为煤焦颗粒的比表面积，CO2为煤焦颗粒表面O2的浓度，n为煤焦燃烧的表观反应阶数，由1.2节中式（18）描述。燃烧产物中CO与CO2的比例由1.3节中的式（20）来描述。这样，就把前面建立的分形煤焦燃烧模型嵌入到了对沉降炉实验的模拟中。

3.3 模型的验证及计算结果分析

运用3.2节中介绍的方法，分别采用本文建立的分形煤焦燃烧模型和传统的本征动力学模型对2.3节中11种煤焦在沉降炉中的燃烧进行了模拟。将实验测量与模型预测的煤焦最终转化率列于表7中。为了对结果进行更直观的分析，将表7中的数据作于图7中。

表7 煤焦最终转化率的实验结果和模拟结果Table 7 Measured and predicted final conversions of all chars

图7 沉降炉实验结果与模拟结果的比较Fig.7 Comparison of DTF experimental results with model predicted results

可以看到，两种模型计算结果的大部分数据点都接近直线y= x，说明对实验所用的大部分煤焦，这两个燃烧速率模型都有较好精度。仔细比较可以发现，对于同一种煤焦，本文构建模型的数据点要比本征动力学模型的数据点更靠近直线y= x，这也就说明本文所构建模型的精度要更高。

以Luoyang、Yongcheng、Hebi和Newlands 4种煤焦为例，图8和图9分别给出了用本文构建的燃烧速率模型模拟得到的煤焦颗粒温度Tp和转化率X随时间变化的曲线。

图8 煤焦燃烧过程中颗粒温度的变化Fig.8 Variation of char particle temperature during combustion

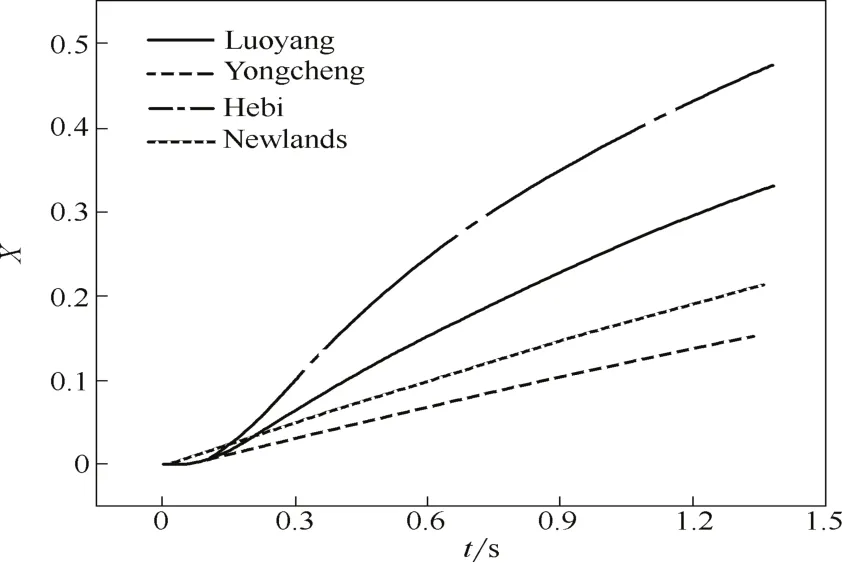
图9 燃烧过程中煤焦颗粒的转化率Fig.9 Char particle conversions during combustion

由图8可知，煤焦颗粒初始为室温（27℃）状态，由于颗粒尺寸很小，沉降炉壁温与周围气流温度很高，颗粒升温很快，随着燃烧的开始，又有大量的热量释放，因而颗粒最高温度会高出壁温许多，最后随着燃烧速率的减慢，颗粒的温度开始缓缓下降。

由图9可知，煤焦转化率随时间不断增大，刚开始增长较快，随后逐渐减慢。不同煤焦的转化率相差很大，这与煤焦本身特性有关，反映在模型中便是煤焦的孔隙结构是否有利于O2向颗粒内部扩散，这可以由模数c的值来度量。

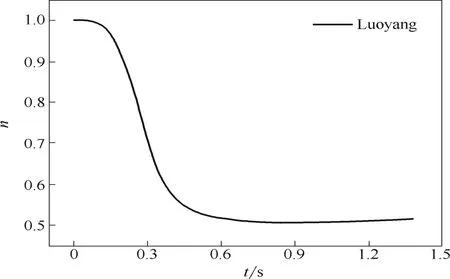
图10 煤焦燃烧过程中表观反应阶数的变化Fig.10 Variation of apparent reaction order during combustion

图10中给出了Luoyang煤焦燃烧过程中表观反应阶数n的变化，其他煤焦情况与此类似。煤焦燃烧之初，颗粒温度较低，燃烧反应处于RegimeⅠ，属于动力学控制区，燃烧速率与煤焦颗粒外表面O2浓度呈正比，因此n的值近似等于1。随着反应温度的升高，燃烧反应渐渐向Regime Ⅱ或Regime Ⅲ过渡，孔隙扩散对煤焦燃烧的影响越来越大，因此，当煤焦颗粒外表面O2浓度发生变化时，煤焦颗粒孔隙内表面的O2浓度变化总会有延迟，这一作用体现到反应阶数上便是使其减小。因此，表观反应阶数n在煤焦燃烧过程中是逐渐减小，最终趋于稳定的。

对于各孔隙结构参数（孔隙率、比表面积、分形维数）和粒径对煤焦燃烧表观速率常数ka的影响，He等[2]已在其论文中分析过了，这里不再赘述。只给出最后结论：表观速率常数ka随着分形维数、比表面积、颗粒粒径的增大而减小，而随着孔隙率的增大而增大。

4 结 论

本文建立了一个综合的煤焦燃烧模型，考虑了颗粒孔隙内扩散与反应的耦合作用，煤焦燃烧过程中表观反应阶数变化和燃烧产物中的CO/CO2比例也有可靠的定量描述。表观速率常数ka随着煤焦颗粒的分形维数、比表面积、粒径的增大而减小，而随着孔隙率的增大而增大。

用热重分析法（TGA）测得11种煤阶跨度较大的煤焦的表观活化能与指前因子，用以确定模型中的待定参数。在沉降炉内对这11种煤焦进行燃烧实验，测得其最终转化率。分别用本征动力学模型及本文所建立的煤焦燃烧模型对这些煤焦的燃烧过程进行模拟，本文所建立的模型预测的转化率与实验数据符合较好，而且比本征动力学模型精度更高，从而证明该模型可以适用于从褐煤到无烟煤的较广煤焦范围。

研究还发现，燃烧过程中煤焦颗粒的最高温度会比周围的环境温度更高，这是由反应放热所致；表观反应阶数n由1开始逐渐减小，并最终稳定下来，这说明反应过程中煤焦孔隙扩散作用随着颗粒温度的升高而不断增强。

符 号 说 明

References

[1] 尧志辉, 旷戈, 林诚, 等. 单颗粒煤焦燃烧反应动力学研究方法[J].化工学报, 2009, 60 (6): 1442-1451. YAO Z H, KUANG G, LIN C, et al. Methodological study on combustion reaction kinetics of single coal char particle [J]. CIESC Journal, 2009, 60 (6): 1442-1451.

[2] HE W, LIU Y, HE R, et al. Combustion rate for char with fractal pore characteristics [J]. Combustion Science and Technology, 2013, 185 (11): 1624-1643.

[3] SMITH I W. The combustion rates of coal chars: a review [J]. Symposium (International) on Combustion, 1982, 19 (1): 1045-1065.

[4] 王芳, 曾玺, 王永刚, 等. 微型流化床与热重测定煤焦非等温气化反应动力学对比 [J].化工学报, 2015, 66 (5): 1716-1722. WANG F, ZENG X, WANG Y G, et al. Comparation of non-isothermal coal char gasification in micro fluidized bed and thermogravimetric analyzer [J]. CIESC Journal, 2015, 66 (5): 1716-1722.

[5] 虞君武, 陈永利, 何榕, 等. FD模型应用于煤热解过程的数值模拟 [J].化工学报, 2014, 65 (9): 3592-3598. YU J W, CHEN Y L, HE R, et al. Numerical simulation of coal pyrolysis using FD model [J]. CIESC Journal, 2014, 65 (9): 3592-3598.

[6] AVNIR D, FARIN D, PFEIFER P. Surface geometric irregularity of particulate materials: the fractal approach [J]. Journal of Colloid and Interface Science, 1985, 103 (1): 112-123.

[7] HE R, SATO J, CHEN C H. Modeling char combustion with fractal pore effects [J]. Combustion Science and Technology, 2002, 174 (4): 19-37.

[8] HE R, XU X, CHEN C, et al. Evolution of pore fractal dimensions for burning porous chars [J]. Fuel, 1998, 77 (12): 1291-1295.

[9] EVERSON R C, NEOMAGUS H W J P, KAITANO R. The random pore model with intraparticle diffusion for the description of combustion of char particles derived from mineral and inertinite rich coal [J]. Fuel, 2011, 90 (7): 2347-2352.

[10] FEI H, HU S, XIANG J, et al. Study on coal chars combustion under O2/CO2atmosphere with fractal random pore model [J]. Fuel, 2011, 90 (2): 441-448.

[11] 费华, 胡松, 向军, 等. 随机孔模型研究煤焦O2/CO2燃烧动力学特征 [J].化工学报, 2011, 62 (1): 199-205. FEI H, HU S, XIANG J, et al. Kinetics of coal char combustion with random pore model under O2/CO2atmosphere [J]. CIESC Journal, 2011, 62 (1): 199-205.

[12] FENG B, BHATIA S K. Variation of the pore structure of coal chars during gasification [J]. Carbon, 2003, 41 (3): 507-523.

[13] 任轶舟, 王亦飞, 朱龙雏, 等. 高温煤焦气化反应的Langmuir-Hinshelwood动力学模型 [J].化工学报, 2014, 65 (10): 3906-3915. REN Y Z, WANG Y F, ZHU L C, et al. Langmuir-Hinshelwood kinetic model of high temperature coal char gasification reaction [J]. CIESC Journal, 2014, 65 (10): 3906-3915.

[14] SADHUKHAN A K, GUPTA P, SAHA R K. Characterization of porous structure of coal char from a single devolatilized coal particle: coal combustion in a fluidized bed [J]. Fuel Processing Technology, 2009, 90 (5): 692-700.

[15] SU J L, PERLMUTTER D D. Effect of pore structure on char oxidation kinetics [J]. AIChE Journal, 1985, 31 (6): 973-981.

[16] BARRANCO R, ROJAS A, BARRAZA J, et al. A new char combustion kinetic model (1): Formulation [J]. Fuel, 2009, 88 (12): 2335-2339.

[17] FORTSCH D, ESSENHIGH R H, SCHNELL U, et al. On the application of the Thiele/Zeldovich analysis to porous carbon combustion [J]. Energy and Fuels, 2003, 17 (4): 901-906.

[18] MA L, MITCHELL R. Modeling char oxidation behavior under Zone Ⅱ burning conditions at elevated pressures [J]. Combustion and Flame, 2009, 156 (1): 37-50.

[19] ROJAS A, BARRAZA J, BARRANCO R, et al. A new char combustion kinetic model (2): Empirical validation [J]. Fuel, 2012, 96: 168-175.

[20] HURT R H, CALO J M. Semi-global intrinsic kinetics for char combustion modeling [J]. Combustion and Flame, 2001, 125 (3): 1138-1149.

[21] LIU Y, HE R. Variation of apparent reaction order in char combustion and its effect on a fractal char combustion model [J]. Combustion Science and Technology, 2015, 187 (10): 1638-1660.

[22] HE W, HE R, ITO T, et al. Numerical investigations of CO/CO2ratio in char combustion [J]. Combustion Science and Technology, 2011, 183 (9): 868-882.

[23] 何威. 煤焦燃烧模型[D]. 北京: 清华大学, 2011. HE W. Study of char combustion model [D]. Beijing: Tsinghua University, 2011.

[24] CAO L, HE R. Gas diffusion in fractal porous media [J]. Combustion Science and Technology, 2010, 182 (7): 822-841.

[25] KNUDSEN M. The law of the molecular flow and viscosity of gases moving through tubes [J]. Annals of Physics, 1909, 28 (3): 75-130.

[26] LIANG Z, HE R, CHEN Q, et al. Fractal generation of char pores through random walk [J]. Combustion Science and Technology, 2007, 179 (3): 637-661.

[27] TOGNOTTI L, LONGWELL J P, SAROFIM A F. The products of the high temperature oxidation of a single char particle in an electrodynamic balance [J]. Symposium (International) on Combustion, 1991, 23 (1): 1207-1213.

[28] BHATIA S K, PERLMUTTER D D. A random pore model for fluid-solid reactions(I): Isothermal, kinetic control [J]. AIChE J., 1980, 26 (3): 379-386.

[29] HE R, SATO J I, CHEN Q, et al. Thermogravimetric analysis of char combustion [J]. Combustion Science and Technology, 2002, 174 (4): 1-18.

Foundation item: supported by the National Natural Science Foundation of China (51176096).

Development and experimental validation of fractal char particle combustion model with effect of various reaction order

LIU Yuting, HE Rong
(Key Laboratory of Thermal Science and Power Engineering of Ministry of Education, Department of Thermal Engineering, Tsinghua University, Beijing 100084, China)

Abstract:A fractal char particle combustion model was developed to study the char combustion mechanism and improve the prediction accuracy of the char combustion characteristics. This model considered the coupling effects of the secondary reactions and gas diffusion within the char pores. The apparent reaction order of char combustion changed with the particle temperature, the O2partial pressure at the particle surface and the particle pore structure parameters instead of keeping constant 1. The primary CO/CO2ratio was obtained by theoretical derivation. The combustion characteristics of eleven different chars were analyzed by a thermogravimetric analyzer (TGA) with their apparent activation energies and pre-exponential factors measured which were used to solve the undetermined model parameters. These chars were also combusted in a drop tube furnace (DTF) and the char samples were collected at the outlet of the DTF. The conversions of these char samples were measured by TGA based on the ash conservation method. The combustion processes of these chars were simulated by this model. The predicted char conversions by this model were matched very well with the measured data and the accuracy was significantly improved compared with the intrinsic model, proving that this model had good accuracy over a wide range of char particles from lignite to anthracite. The study also showed that the apparentbook=340,ebook=348reaction order of char combustion first decreased and then gradually stabilized in the char combustion process.

Key words:char combustion; model; simulation; drop tube furnace; experimental validation; apparent reaction order; fractals

Corresponding author:Prof. HE Rong, rhe@mail.tsinghua.edu.cn

基金项目：国家自然科学基金项目（51176096）。

中图分类号：TQ 534

文献标志码：A

文章编号：0438—1157（2016）01—0339—10

DOI：10.11949/j.issn.0438-1157.20150934