考虑波浪自由表面作用的海底管道局部泥沙冲刷数值研究

刘名名， 吕 林， 滕 斌， 唐国强

(大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024)



考虑波浪自由表面作用的海底管道局部泥沙冲刷数值研究

刘名名， 吕 林， 滕 斌， 唐国强

(大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024)

该文利用有限元方法，在任意拉格朗日-欧拉(Arbitrary Lagrangian-Eulerian，ALE)观点下求解不可压缩粘性流体的Navier-Stokes方程和泥沙输运方程，建立了可充分考虑波浪自由表面影响作用的海底管道局部冲刷数值分析模型。其中，流动的湍流效应通过SST k-ω模型进行模拟，波浪自由表面及底床变形通过动网格方法进行实时界面追踪，模型同时考虑了悬移质输沙和推移质输沙。通过与已发表研究成果的对比验证，该文所建立的模型具有良好的数值精度。在进一步考虑波浪自由表面效应的基础上，对海底管道局部冲刷问题开展了数值研究，考察了入射波高和波浪周期对局部冲刷以及管道受力的影响作用。该文所建立的数值模型是对以往长期采用简化的振荡流模型(忽略波浪自由表面效应)进行海底管道局部冲刷数值研究的重要发展。

波浪；海底管道；局部冲刷；自由表面；数值模拟

0 引言

海底管道是进行海洋油气资源开发的重要工程设施，铺设于海底的管道在水流、波浪等复杂海洋环境条件作用下，极易发生局部冲刷、管道悬空和涡激振动疲劳破坏，这将给海洋油气生产企业带来巨大的经济损失，甚至引起严重的海洋环境污染。因此，有必要对海底管道的局部冲刷问题展开研究。

针对海底管道局部泥沙冲刷问题，Breuser[1]认为，当外部流动速度小于某一临界流速时，局部冲刷深度会随着流速的增大而不断增大，当达到临界流速之后，流速的增大不会导致冲刷深度的进一步增加。Kjeldsen[2]等对海底管道局部泥沙冲刷开展了实验研究，结果表明，管道的几何尺寸、来流流速等都会对冲刷深度产生较大的影响，并基于实验结果建立了海底管道局部冲刷深度与管道直径及来流流速之间的经验关系。Bijker和Leeuwestein[3]对具有一定埋深的海底管道局部冲刷问题开展了实验研究，结果表明，平衡冲刷深度随着埋深比的增大而减小。Ibrahim和Nalluri[4]通过对实验结果的分析指出，应将冲刷问题分为清水冲刷(θ < θcr)和动床冲刷(θ > θcr)两类(θ为泥沙底质的希尔兹参数，θcr为临界希尔兹参数)。Sumer和Fredsфe[5]分别对清水冲刷和动床冲刷这两类问题开展了实验研究，结果表明，在清水冲刷情况下，冲刷深度会随着底床切应力系数(Sheilds parameter)的变化而发生明显变化，在动床冲刷的情况下，冲刷深度对希尔兹参数的依赖性不大。

除实验手段外，数值模拟也是研究管道局部冲刷的重要手段。Hensen[6]通过势流模型，对单向流作用下的海底管道局部冲刷问题开展了研究，数值结果表明，势流模型能够较为准确地预测管道下方的最大冲刷深度，但对管道周围冲坑形态的模拟结果与实验值存在较大的差别。Li和Cheng[7]认为，势流模型的这一缺陷主要是由于无法模拟管道后方的旋涡脱落所致，因此，考虑涡旋运动对管道局部冲刷的影响作用，Li和Cheng[8]建立了基于Navier-Stokes方程的粘性流模型。该模型中基于底切应力平衡的概念来模拟稳定平衡剖面，虽然获得了与实验观测一致的平衡冲刷剖面，但是不能预测管道周围泥沙冲刷的时间发展历程。Liang和Li[9]发展了能够描述冲刷剖面随时间发展的局部冲刷模型，并基于该模型对管道自埋问题开展了数值研究。Zhao和Cheng[10]进一步对单向流作用下，振动管道周围的局部冲刷问题开展了数值研究。对于波浪作用下海底管道局部冲刷问题的数值研究，目前只有少量的研究成果，具有代表性的研究工作为Liang和Cheng[11]所建立的振荡流数值分析模型。在该模型中，波浪运动被简化为振荡流，忽略了自由表面对管道冲刷的影响作用，数值结果与Sumer和Fredsфe[12]实验结果的对比表明，简化的振荡流模型能够对管道局部冲刷给出比较合理的预报。但是，当波浪的非线性作用显著时，完全忽略自由表面作用可能会引起较大的误差。由于振荡流模型是一个水质点运动严格水平对称的模型，对于受地形显著影响或存在流量净输运的问题都不再适用。

目前，对于水流作用下的海底管道局部泥沙冲刷问题，国内外学者已经通过实验或数值方法取得了丰富的研究成果，研究工作已日趋完善。而对于波浪作用下的海底管道局部冲刷问题，现阶段主要依靠实验手段，在模型比尺相似方面还存在很大的技术挑战。相关的数值分析工作，主要依靠简化的振荡流模型，其适用范围还存在较大的限制。因此，有必要建立能够全面考虑自由表面影响作用的海底管道局部冲刷数值分析模型，通过开展详细的数值分析，进一步认识泥沙输运过程的物理机理及平衡剖面的演化特征，从而为海底管道的设计、施工及安全服役提供有力的科学依据及技术参考。

1 数值模型

1.1 流动控制方程

在任意拉格朗日-欧拉(ALE)观点下，不可压缩粘性牛顿流体的雷诺平均Navier-Stokes方程，可写成如下的形式：

(1)

(2)

(3)

该文采用SST k-ω(Menter和Menter)[13，14]湍流模型对上述流动控制方程进行封闭。SST k-ω湍流模型的对流输运方程为：

(4)

(5)

1.2 数值造波与消波

该文通过在入流边界指定速度和波高的方法进行数值造波。线性波的波面升高η可以写为：

(6)

式中：H为入射波波高；σ为波浪的圆频率，σ= 2π/T，T为波浪周期。

根据线性波理论，入流处的速度可以通过以下表达式得到：

(7)

(8)

式中：k为波数；d为水深。

对于二阶Stokes波而言，波面升高η为：

(9)

速度为：

(10)

(11)

出流端采用Sommerfeld边界条件：

(12)

式中：f代表速度、压力等物理量；cw为波浪相速度。

为更好的消除反射波，该文采用Sommerfeld边界条件的同时，在出流端采用与Zhao等[15]相同的阻尼层方法吸收波浪。

1.3 自由表面及底床动边界

波浪自由表面需要同时满足运动学和动力学边界条件，在忽略空气作用条件下，有

(13)

式中：us为波浪自由表面的切线速度分量；n为指出流体的外法线单位矢量。

由泥沙局部冲刷引起的地形变化，可通过以下的底床变形程描述：

(14)

式中：yb为底床高程；λs为孔隙率；qb为推移质输沙率；qs为悬移质输沙率。

1.4 泥沙输运方程

悬移质输沙率可以通过如下的方式求解：

(15)

式中：qs为悬移质输沙率；ys为波浪自由面的高度；c为泥沙颗粒的浓度；ya为悬移质输沙和推移质输沙的分界高度，文中取ya= 2.0d50，d50为泥沙颗粒的中值粒径。

泥沙颗粒的浓度c通过如下的悬移质浓度扩散方程得到：

(16)

式中：σc为湍流的Schmidt数，在该文的计算中取1.0；ws为泥沙颗粒的沉降速度，通过Richardson和Zaki[16]公式计算：

(17)

式中：m = 5.0，ws0根据Soulsby[17]公式给出：

(18)

式中：D*为无量纲化的泥沙粒径，

(19)

式中：s为泥沙密度与流体密度的比值。

推移质输沙率采用Van Rijn[18]公式进行计算：

(20)

式中：qb为推移质输沙率，参数T0的定义如下：

(21)

式中：τ0为底床切应力；ρs为泥沙密度；ρ为流体密度；θ = τ0/[gd50/(ρs-ρ)]为希尔兹参数，其临界值θcr(临界希尔兹参数)的表达式如下：

(22)

式中：α为局部地形坡度，φ为泥沙休止角，θcr0可以通过Soulsby和Whitehouse[19]推荐的公式求得，即：

(23)

1.5 网格更新

该文采用ALE观点下的动网格方法，对波浪自由表面和底床变形进行准确的追踪模拟。在完成每一个时间步计算后，由于波面和底床位置发生改变，需要对内部计算网格进行实时更新。在进行网格运动位移计算时，将计算域假设成为一个弹性体[20]，并通过求解弹性方程来确定网格节点在下一时刻的位置。根据弹性理论，应力张量σ满足如下的方程：

(24)

σ与应变ε的关系为：

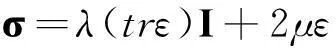
(25)

λ和μ为Lame常数，并有：

(26)

式中：S为待求的节点位移向量。

在计算域的外边界(入流边界、出流边界)，节点的水平位移和垂向位移均为零。而在自由表面和底床，节点位移分别通过求解自由表面方程和底床变形方程得到，由此构成上述控制方程的边界条件。

当通过式(24)得到单元的节点位移后，单元节点在下一时间步的坐标可更新为：

(27)

式中：Si为单元节点位移在第i个坐标分量。

在该文中，新的网格节点运动速度通过文献[21]的方法进行计算:

(28)

2 模型验证

2.1 线性波和二阶Stokes波的生成与传播

为了验证该文所建立的数值模型能够准确描述波浪的生成与传播问题，图1和图2分别给出了该文数值结果与线性波及二阶Stokes波解析解的对比情况。计算中，线性波波高H = 0.04 m、周期T = 1.2 s、水深d = 0.5 m，二阶Stokes波的波高H = 0.1 m、周期T = 1.6 s及水深d = 0.5 m。

通过图1和图2可知，该文计算得到的数值结果与解析解吻合较好，说明该文所建立的模型在模拟线性波浪、非线性波浪的传播问题中都具有良好的数值精度。

图1 线性波的数值验证(距离造波边界10.0 m处波面时间历程线) 图2非线性二阶Stokes波的数值验证(距离造波边界10.0 m处波面时间历程线)

2.2 波浪作用下海底管道局部冲刷

Sumer和Fredsфe[12]对波浪作用下的海底管道局部冲刷问题开展了实验研究。实验中，水深为40 cm，管道铺设在13 cm厚度的沙床上，波浪参数以及泥沙特性参数见表1。需要说明的是，在Sumer和Fredsфe[12]的原始文献中，只给出了入射波的周期和近底处的最大水平流速，而没有给出实验中的入射波波高。该文在开展数值模拟时，根据波浪周期和近底流速，通过二阶Stokes波理论来估算入射波周期，从而获得与Sumer和Fredsфe[12]实验相同的波浪周期及近底最大流速。

表1 Sumer和Fredsфe实验中的波浪参数及泥沙特性参数表

图3给出了不同时刻计算得到的冲刷剖面与Sumer和Fredsфe的实验结果对比情况。通过图3可以看出，该文计算得到的冲刷深度、冲刷范围以及冲刷剖面在t = 5 min和55 min两个代表性时刻均与实验观测结果吻合良好，进一步证明了该文所建立的数值模型的可靠性。

图3 波浪作用下海底管道局部冲刷剖面

3 波浪作用下海底管道局部冲刷的数值研究

利用前述建立的数值模型对波浪作用下海底管道局部冲刷问题开展数值研究，研究中考虑不同入射波波高和周期下，海底管道的局部冲刷以及受力问题。采用的计算参数为：水深d = 0.4 m；波高H = 0.08 m、0.10 m和0.12 m；入射波周期T∈[1.6 s, 3.0 s]，间隔为0.2 s；管道直径D=50 mm；泥沙颗粒中值粒径d50= 0.18 mm。

图4以周期T = 2.8 s为例，给出了不同入射波波高条件下，海底管道的平衡冲刷剖面。从图4中可以看出，随着入射波波高增大，管道附近的冲坑整体变深。入射波周期也是影响管道周围局部冲刷的另一个重要参数，图5以波高H = 0.1 m为例，给出了不同入射波周期下，管道周围的平衡冲刷剖面图。从图5中可以看出，随入射波周期的增大，管道下方的最大冲刷深度逐渐增大，并且最大冲深出现的位置向管道上游偏移。此外，波浪周期对管道周围冲坑的范围也有较大的影响作用，较大的波浪周期会导致更大的冲刷范围。

图4 不同入射波高下管道周围平衡冲刷剖面(T= 2.8 s) 图5 不同波浪周期下管道周围平衡冲刷剖面(H= 0.1 m)

图6 管道最大冲深随波浪KC数的变化情况

以上的数值模拟结果表明，入射波浪的波高和周期都会对管道周期的局部冲刷产生较大的影响。为综合反映波高和周期的联合作用，该文基于数值模拟结果给出了管道正下方冲刷深度随KC数的变化情况，如图6所示，其中：KC数定义为KC = UT/D，U为底床处最大流速，T为波浪周期。Sumer和Fredsфe通过物理模型实验研究发现，波浪作用下海底管道附近的相对冲刷深度与KC数之间满足如下的关系：

(29)

从图6可以看出，该文得到的数值结果与Sumer和Fredsфe的经验公式吻合良好，随着KC数的增大，管道正下方的冲坑深度也随之增大。

波浪作用下悬空海底管道的受力是影响海底管道的在位稳定性的重要因素。以下将对局部冲刷达到稳定状态后，海底管道的波浪力特性开展数值研究。图7以入射波波高H = 0.1 m、波浪周期T = 1.6 s为例，分别给出了管道所受到的水平力及垂向力的时程曲线。对比图7(a)和图7(b)可知，作用于管道上的水平力幅值要远大于垂向力的幅值，并且水平力的时间历程线较垂向力相对规则。为获得管道受力的频率特性，图8给出水平力和垂向力的傅里叶分析结果。从图8(a)中可知，水平力的主控频率与波浪频率相同，其它的频率成分的响应幅值远小于主控频率，且均为入射波浪频率的整数倍。从图8(b)中可知，垂向波浪力的主控频率为波浪频率的2倍，其中1、3、4倍波频的响应幅值约为主控频率下的1/3，对总体垂向波浪力的作用不可忽视。

图7 管道所受波浪力的时间历程线(H= 0.1 m，T = 1.6 s)

图8 管道受力的FFT分析(H= 0.1 m，T= 1.6 s)

图9进一步给出了作用在管道上的无量纲波浪力的均方根值随KC数的变化情况。从图9中可以看出，在该文所计算的KC数范围内，管道所受水平力和垂向力的均方根值与KC数均呈线性关系。

图9 管道受力随KC数的变化情况

4 结论

针对波浪作用下的海底管道局部冲刷和受力问题，建立了可考虑波动自由表面作用的数值分析模型。该模型通过求解不可压缩粘性流体的Navier-Stokes方程、SST k-ω湍流方程以及泥沙输运方程来模拟海底管道的局部冲刷过程。其中，由底床冲刷变形以及波浪自由表面所引起的动边界通过任意拉格朗日-欧拉方法进行实时追踪。通过对比分析，表明该模型能够对管线局部冲刷问题进行准确预测，从而克服了长期沿用简化的振荡流模型，忽略非线性波浪自由表面效应的局限性。

基于该文所建立的数值模型，重点考察了波高和周期对管道局部冲刷以及受力的影响作用。数值模拟结果表明：随着入射波波高和周期的增大，管道局部冲刷深度加大，相对冲刷深度S/D与波浪KC数之间满足S/D=0.1KC0.5的近似关系，这与Sumer和Fredsфe的实验观测结果是一致的；当局部冲刷达到平衡状态后，作用在管道上的无量纲水平力和垂向力均随KC数呈线性关系增长，其主控频率分别体现在1倍和2倍波浪频率上。

[1] Breusers H N C. Local scour near offshore structures[M]. Delft Hydraulics Laboratory, The Netherlands, 1972.

[2] Kjeldsen S P, Gjorsvik C, Bringaker K G, et al. Local Scour near offshore pipelines[C]. Proceedings of the Second International Conference on Port and Ocean Engineering Under Arctic Conditions, University of Iceland,1973．

[3] Bijker E W, Leeuwestein W. Interaction between pipelines and the seabed under influence of waves and currents, in seabed mechanics[M]. Springer, Netherlands, 1985.

[4] Ibrahim A, Nalluri C. Scour prediction around marine pipelines[C]. Proceedings of 5th International Symposium on Offshore Mechanics and Arctic Engineering, ASME, New York, 1986．

[5] Sumer B M, Fredsфe J. The mechanics of scour in the marine environment[M]. World Scientific, Singapore, 2002.

[6] Hansen E A, Fredsae J, Mao Y. Two dimensional scour below pipelines[C]. Proceedings of 5th International Symposium on Offshore Mechanics and Arctic Engineering, ASME, Tokyo, Japan, 1986.

[7] Li F J, Cheng L. Numerical model for local scour under offshore pipelines[J]. Journal of Hydraulic Engineering. 1999, 125(4): 400-406.

[8] Li F J, Cheng L. Prediction of lee-ewake scouring of pipelines in currents[J]. Journal of Waterway, Port, Coastal and Ocean Engineering, 2001, 127(2): 106-112.

[9] Li F J, Cheng L. Modelling of local scour below a sagging pipeline[J]. Coastal Engineering, 2003, 45(2): 189-210.

[10] Zhao M, Cheng L. Numerical investigation of local scour below a vibrating pipeline under steady currents[J]. Coastal Engineering, 2010, 57(5): 397-406.

[11] Liang D F, Cheng L. Numerical model for wave-einduced scour below a submarine pipeline[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2005, 131(5): 193-202.

[12] Sumer B M, Fredsфe J. Scour below pipelines in waves[J]. Journal of Waterway Port Coastal and Ocean Engineering,1990, 116 (3): 307-323.

[13] Menter F R. Two-eequation eddy-eviscosity turbulence models for engineering applications[J]. AIAA Journal,1994, 32(8): 1598-1605.

[14] Menter F R, Kuntz M, Langtry R. Ten years of industrial experience with the SST turbulence model[M]. Turbulence, Heat and Mass Transfer. Begell House, Inc., 2003.

[15] Zhao M, Teng B, Tan L. A finite element solution of wave force on submerged horizontal circular cylinder[J]. China Ocean Engineering, 2004, 18(3): 335-346.

[16] Richardson J F, Zaki W N. Sedimentation and fluidization: Part I[J]. Transactions of the Institution of Chemical Engineers,1954, 32(1), 35-53.

[17] Soulsby R. Dynamics of marine sands[M]. Tomas Telford, London,1997.[18] Van R L C. Mathematical modeling of morphological processes in the case of suspended sediment transport[D]. Delft University of Technology, Delft, The Netherlands,1978.

[19] Soulsby R, Whitehouse R. Threshold of sediment motion in coastal environments[C]. Proceedings of the Pacific Coasts and Ports Conference. Christchurch, New Zealand, 1997.

[20] Johnson A A, Tezduyar T E. Mesh update strategies in parallel finite element computations of flow problems with moving boundaries and interfaces[J]. Computer Methods in Applied Mechanics and Engineering, 1994, 119(4): 73-e94.

[21] Guermond J L, Quartapelle L. On stability and convergence of projection methods based on pressure Possion equation[J]. International Journal for Numerical Methods in Fluids, 1998, 26(6): 1039-1053.

Numerical Investigation of Local Scour Around Pipeline under Surface Waves

(State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology, Liaoning Dalian 116024, China)

A two-dimensional finite element numerical model is developed to predict the local scour around submarine pipelines induced by orbital fluid motion of surface water waves. The numerical model is based on the two-dimensional Navier-Stokes equations with Shear-Stress Transport (SST) k-ω turbulent closure. Both suspended load and bed load sediment transportations are considered. The moving boundaries of wave free surface and the evolution of the seabed due to local scour are tracked by using Arbitrary Lagrangian-Eulerian (ALE) method. Comparisons with available theoretical and experimental data show satisfactory agreements. The proposed numerical model is then used to investigate the nonlinear wave-induced local scour around pipelines. The effects of wave height and wave period on the local scour and the wave forces on the pipelines are examined. The present numerical model is a further development for the investigation of local scour around pipeline compared with oscillatory flow model.

water wave； submarine pipeline； local scour； free surface； numerical simulation

2015-07-23

国家自然科学基金(51409035，51279029)；国家“973”计划(2014CB046803)。

刘名名(1986-)，男，博士研究生。

1001-4500(2016)01-0042-08

P75

A