大型回转窑筒体强度分析

田国富，唐媛媛，周学飞，张西栋，高 峰

(1.沈阳工业大学机械工程学院，辽宁 沈阳110870；2.北方重工集团有限公司矿山机械分公司，辽宁 沈阳110141)

大型回转窑筒体强度分析

田国富1，唐媛媛1，周学飞2，张西栋1，高 峰1

(1.沈阳工业大学机械工程学院，辽宁 沈阳110870；2.北方重工集团有限公司矿山机械分公司，辽宁 沈阳110141)

回转窑是一种大型的冶金设备。为了保证回转窑筒体的强度，依据梁理论和有限元的方法，对不同温度和不同壁厚下的回转窑筒体强度进行了分析，得到了不同工况下的筒体的应力、应变和挠度。结果表明，在不同条件下，筒体强度均在安全域度之内。对回转窑筒体强度的分析验证了梁理论和有限元方法在类似力学模型求解中的有效性，为整机和筒体设计优化奠定了理论基础。

回转窑；梁理论；应力分析

0 前言

回转窑在冶金、化工、水泥和环保行业被广泛应用，如图1所示，回转窑主要是由筒体、轮带、齿圈、托轮等组成[1]，其中筒体是回转窑的核心部件。回转窑的筒体是由厚度不同的钢板焊接而成，筒体直径一般4～5 m，长度50～100 m，因为长度较长，所以一般有着4～9档的支撑[2]。回转窑工作时，筒体内部温度较高，为了避免筒体表面温度过高，在筒体内部砌有耐火砖。筒体、耐火砖和物料的总重量可达千吨，托轮和筒体承受着较大的压力。回转窑具有大口径、大跨距、复杂载重和内部高温的特点，要求筒体有足够的刚度。回转窑筒体是由厚度为20～90 mm的钢板卷制而成。如果筒体的壁厚整体减少1 mm，大概可以节约5～7 t的钢材。减少壁厚是降低成本，节约钢材最有效的方法。因此本文主要校核了原壁厚、壁厚减2 mm和壁厚减4 mm情况下筒体的强度，又因为筒体表面有一定的温度，此温度不能忽略，同样对不同温度下的筒体强度进行了校核。以现有的筒体厚度为28 mm(最薄处)的回转窑为例，在此基础上进行不同壁厚和不同温度下的筒体强度的校核实验。

图1 回转窑实物图Fig.1 Rotary kiln

1 采用梁理论对筒体的受力进行分析

采用梁理论[3]对回转窑进行分析时，假设筒体是水平的连续梁，不考虑筒体的倾斜，不计物料重心对窑体轴线的影响，对所有的重力按均布载荷加载到简支梁上(包括筒体、耐火砖和物料)，将齿轮等效为集中载荷作用在筒体上。

1.1 梁理论下的筒体应力分析

1.1.1 简化模型求各档弯矩

已知回转窑筒体重650 t，耐火砖重888 t，物料重222 t，齿圈重20 t。筒体材料为Q235，轮带材料ZG35CrMo。简化筒体模型为图2所示简支梁。图中l1=4 m，l2=22.9 m，l3=25.8 m，l4=26.8 m，l5=11.9 m，δ1=45 mm，δ2=30 mm，δ3=30 mm，δ4=28 mm，δ5=28 mm ，L1=5 m，L2=25 m，L3=28 m，L4=29 m，L5=13 m，a=4 m。

图2 回转窑连续梁模型Fig.2 Continuous beam model of rotary kiln

支撑处的距离分别为2.2 m、2 m、2 m、2 m，厚度为75 mm。由于支撑处占的比例较小，所以图2中未做标注。

窑头集中力：P=qL1=0.88 MN·m

(1)

(2)

窑尾集中力：P=qL5=2.288 MN

(3)

(4)

采用三弯矩法计算各档弯矩[4]。

2档方程式：

(5)

3档方程式：

(6)

解得M2=-12.2746 MN·m，M3=-11.4007 MN·m

利用三弯矩法解出弯矩后，利用各档弯矩图(图3到图5)和所得的弯矩计算支座反力。

图3 1-2跨支撑简图Fig.3 1-2 support of cross

(7)

(8)

图4 2-3跨支撑简图Fig.4 2-3 support of cross

(9)

(10)

图5 3-4跨支撑简图Fig.5 3-4 support of cross

(11)

(12)

各档支座反力：R1=3.184 MN；R2=4.6198 MN；R3=5.0365 MN；R4=4.9597 MN。

根据所求的支座反力，可以求出各跨间的最大弯矩点：x1=13.09 m；x2=14.34 m;x3=13.82 m。

分别求出各跨中间的最大弯矩，即

(17)

(18)

(19)

1.1.2 筒体应力的计算

筒体的应力计算公式为

(20)

滚圈中心线处KS=1；其他部位KS=0.9。KT与筒体温度有关，筒体温度为250 ℃，KT=0.83[5]

W与厚度δ有关，即

(21)

筒体的厚度只有在筒体应力计算的公式中有体现，只要重新计算W，在带入筒体应力公式，就可计算出不同壁厚的应力大小。代入不同的W，得到的表1。

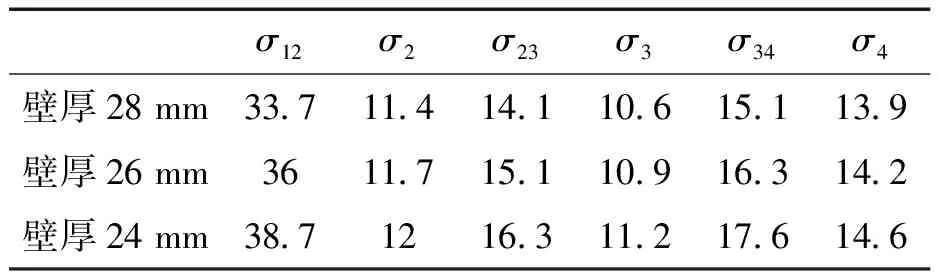
表1 不同厚度下的筒体应力大小/MPa

1.2 筒体挠度分析

采用梁理论校核筒体强度时，不仅要考虑筒体的应力，而且要分析筒体的变形。梁理论分析筒体的变形，主要是分析筒体的挠度。筒体表面有一定的温度，则取E=1.88×1011Pa(筒体表面温度300 ℃)。挠度与惯性矩有关，不同壁厚下的惯性矩不同(a为内外径的比)。

(22)

不同壁厚下的挠度计算公式一样，只有惯性矩大小会改变，以壁厚28 mm的筒体不同段的挠度为例。

在L1段：

I1=1.77 m4

(23)

挠度：

(24)

L2和L3段筒体壁厚相同，但L3段长度较长，且有齿轮的作用，L3段挠度大于L2段的挠度，所以只对L3段做计算。

I3=1.17 m4

(25)

(26)

(27)

y2=y31+y32=6.4369×10-3m

(28)

L4段和L5段的分别为

I4=1.09 m4

(29)

(30)

I5=1.09 m4

(31)

(32)

计算不同壁厚下的挠度，列出表2。

表2 不同壁厚下的回转窑筒体挠度

2 采用有限元方法进行分析

2.1 模型的建立

采用梁理论是通过将筒体简化成简支梁的力学模型再计算，忽略了筒体的直径，由于筒体的长度远大于直径，采用梁理论计算是合理的。但采用梁理论计算是也存在一定不足，采用梁理论计算时，载荷视作均布载荷，而实际筒体载荷的部分在筒体的下半部[6]。采用有限元方法更能反应出载荷的实际加载情况，因此本文也采用有限元方法对筒体做进一步分析，以弥补梁理论在计算时的不足之处。

按照项目方提供的图纸，建立不同厚度的有限元模型，轮带与筒体间通过垫板连接，筒体内部建筋板，保证筒体的刚度和强度，支撑处采用V型块模拟托轮，如图6所示。因为只考虑壁厚对应力的影响，所以部分零件做简化处理。

图6 回转窑轮带模型Fig.6 The rotary kiln tie model

2.2 加载求解

图7是将零件导入Ansys Workbench ，定义材料属性，弹性模量取E=1.88×1011Pa。进行网格划分，网格单元尺寸是200 mm。

图7 回转窑有限元模型图Fig.7 Finite element model of rotary kiln

由于不考虑筒体的倾斜和转动，加载时只需限制V型块的Y方向位移，筒体重力和耐火砖的总重量作用到筒体表面，物料重量作用在筒体下表面，如图8所示。

图8 回转窑筒体受力分析图Fig.8 Stress analysis of rotary kiln cylinder

加载求解，得到了不同壁厚下的应力和应变云图，如图9和图10是筒体壁厚28 mm的应力应变图。改变筒体的壁厚，再重新加载，得到不同壁厚的应力和应变的最大值。

图9 筒体壁厚28 mm应力云图Fig.9 Stress cloud of 28 mm thickness cylinder

图10 筒体壁厚28 mm应变云图Fig.10 Strain cloud of 28 mm thickness cylinder

3 不同温度下数据对比分析

回转窑的内部进行着氧化还原反应，内部温度可达1 450 ℃，即使窑体内部砌有耐火砖，但表面也可达250 ℃左右。在高温下不仅筒体的弹性模量等参数发生变化，材料的许用应力应变的值也发生变化，所以有必要进行不同温度下的分析。改变梁理论和有限元分析时有关温度的参数，再进行分析，得到不同温度下应力、应变和挠度的值，见表3～5，分别是筒体温度100 ℃、250 ℃和300 ℃下各结果的值。材料的许用应力随温度的升高而降低，如表6是不同温度下弹性模量和许用应力的值。将结果与不同温度下材料的许用应力的值进行比较，发现结果均满足要求。

表3 100 ℃筒体分析结果

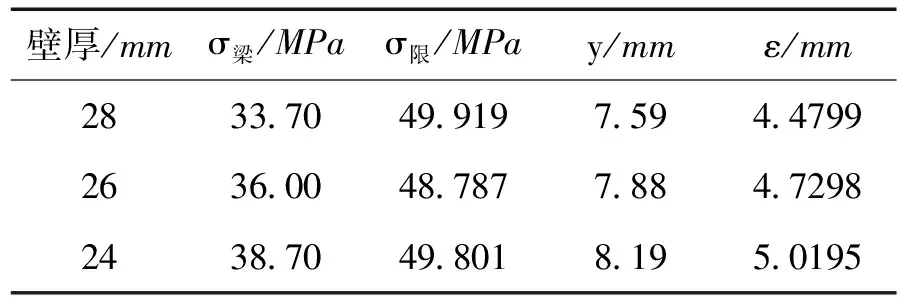
表4 250 ℃筒体分析结果

表5 300 ℃筒体分析结果

表6 不同温度下的弹性模量和许用应力表

4 结论

本文采用梁理论和有限元两种方法，分别对不同壁厚的回转窑筒体的强度进行了分析，将得到的应力应变值与许用值进行比较，均满足要求。在具体工况下筒体表面存在250 ℃到350 ℃温度变化，因此本文对100 ℃、250 ℃和300 ℃下的不同壁厚的应力应变进行了分析，分析结果满足强度要求。筒体强度按照两种方法的分析结果表明均满足要求，为后续筒体整体优化提供了理论基础。

[1] 陈明非. 大型回转窑支撑部位应力与应变有限元分析[J].机械设计与制造, 2014(6):62-64.

[2] 李学军,刘义伦,肖友刚. 大型多支承变截面回转窑支承系统力学行为分析[J]. 重型机械, 2002,5(7):19-20.

[3] 王和慧,谢可迪,陈一凡,等.大型回转窑支撑系统的力学行为分析[J].机械强度,2010,34(4)：606-616.

[4] 张波.大型回转窑筒体力学分析与计算[D].北京：北方工业大学.2012：13-19.

[5] 《回转窑》编写组.回转窑设计、使用与维护[M].冶金工业出版社.1978:240-248.

[6] 董艳芳.回转窑筒体变形有限元分析.武汉:武汉理工大学.2014：30-35.

Strength analysis of large-scale rotary kiln

TIAN Guo-fu1，TANG Yuan-yuan1，ZHOU Xue-fei2, ZHANG Xi-dong1,GAO Feng1

(1.School of Mechanical Engineering, Shenyang University of Technology, Shenyang 110870, China；2. The North Heavy Industry Group Limited mining machinery branch，Shenyang 110141, China)

Rotary kiln is a large metallurgical equipment. In order to ensure the strength of the rotary kiln cylinder, the paper is based on the beam theory and the finite element method to analyze the cylinder strength under different temperature and different wall thickness, the stress, strain and deflection of the cylinder are obtained under different conditions. The results show that the cylinder strength is within the safety range of the different working conditions. Strength analysis of rotary kiln to verify the beam theory and finite element method similar effectiveness in solving the mechanical model, and it can lay a theoretical foundation for the design optimization of the whole machine and the cylinder.

rotary kiln；beam theory；stress analysis

2016-01-05；

2016-02-19

沈阳市科技创新专项资金-工业科技攻关专项(F15040200)。

田国富(1968-)，男，吉林长春人，博士后，副教授，研究领域为机械系统的CAD/CAE技术、工程车辆设计与试验等

唐媛媛(1990-)，女，辽宁沈阳人，硕士研究生，研究方向为机械设计及理论。

TH123.4

A

1001-196X(2016)04-0061-05