对永磁同步电主轴的齿槽转矩的分析
2016-03-15钟双双于慎波
钟双双,于慎波
(沈阳工业大学 机械工程学院,辽宁 沈阳 110870)
对永磁同步电主轴的齿槽转矩的分析
钟双双,于慎波
(沈阳工业大学 机械工程学院,辽宁 沈阳 110870)
永磁同步电主轴被广泛使用在各种高性能的速度和位置控制系统中,但为了保证其高质量的运行,应降低齿槽转矩。文章分析了齿槽转矩产生原因和削弱方法,提出了梯形磁体和阶梯磁体两种永磁体结构,研究其对永磁同步电主轴的齿槽转矩的影响。并运用Ansys对这两种永磁体结构的永磁同步电主轴进行仿真。最后针对仿真所得的数据,运用Matlab对其进行计算、分析和对比。结果表明,在不影响永磁同步电主轴平均转矩等运行性能的前提下,适当的梯形永磁体的倾斜角度和阶梯永磁体的阶梯高,会使齿槽转矩的最大值和基波的幅值降低。
永磁同步电主轴;齿槽转矩;梯形磁体;阶梯磁体
0 前言
随着高性能的永磁材料的发展和制造技术的进步,永磁同步电主轴已经被广泛的应用在各种场合中,如机床,工业机器人等。永磁同步电主轴具有非常广泛的应用前景[1]。但是,由于永磁同步电主轴的转矩脉动可以导致电主轴的机械振动和噪声等问题,因此,最小化波动是永磁同步电主轴在设计时必须考虑的因素。电主轴本身的转矩脉动源头有三个:(1)齿槽转矩;(2)d轴和q轴中气隙磁导之间的差异;(3)气隙中磁通密度波形的失真。而齿槽转矩是最重要的转矩脉动源头[2]。所谓齿槽转矩是由安装在转子上的永磁体与定子的各向异性的相互作用引起的。国内外学者对齿槽转矩进行了很多研究,并提出了多种降低齿槽转矩的方法,如运用分数槽、引入辅助槽、磁极不对称和选择最优的极弧极距比[3-6],倾斜转子磁体和定子齿[7-8],磁极偏移[1],分段转子[9]等方法。
本文以一台16极36槽矩形永磁体的永磁同步电主轴作为研究对象,从理论上分析了永磁同步电主轴齿槽转矩的产生机理,通过更改永磁体的形状,用Anasys对其进行仿真,并用matlab对仿真所得数据进行计算、分析和对比。从而可以得到降低齿槽转矩最大值和基波幅值的最佳结构。
1 齿槽转矩的解析表达式
在没有施加电流驱动的条件下,齿槽转矩也会存在。它是由安装在转子上的永磁体和由定子绕组槽引起的各向异性之间的相互作用产生的。在旋转过程中,由于各向异性的磁场能量的变化,从而产生齿槽转矩,如式(1)所示[10]。
(1)
式中,Tcog为齿槽转矩;θm为转子的机械角度;Wm为磁体能量。
在电机运行时,齿槽转矩会产生零静功,但它会作为一个干扰叠加在所产生的电磁转矩中。
由于齿槽转矩是由转子上的永磁体和定子槽口的相互作用所引起的,所以齿槽转矩的周期与槽极数有关。
在一个槽间距旋转,齿槽转矩周期数Nsp是一个非常重要的指标,因为它能提供基本齿槽转矩波形的空间位移信息[10]。显然,如果基本转矩的相位是不同的,那么所产生的齿槽转矩就是最小的。
(2)
式中,Nsp为在一个槽间距旋转时齿槽转矩周期数;p为极对数;HCF为最大公约数。
齿槽转矩的空间周期Tsp可以表示为
(3)
式中,Tsp是齿槽转矩的空间周期,LCM是最小公倍数。
如式(3)所示,Tsp与Nsp成反比。Nsp最小值是1,当为最小值时,基本转矩的波形是相同的相,由此产生的齿槽转矩的值是最大的。由于基本转矩波形是沿着槽间距分布的,所以越大的Nsp值会产生越小的齿槽转矩。
齿槽转矩被表达成傅里叶级数的形式为
(4)
由于磁场的能量可以表示为磁导函数和磁动势平方,所以许多用来减小主要谐波的幅值的方法都是通过作用这些物理量中的一个或两个。
2 永磁同步电主轴的结构模型和基本参数
文中以16极36槽的永磁同步电主轴为模型,此永磁同步电主轴是分数槽绕组,且每极每相的槽数小于1(q<1),且永磁体为矩形,结构如图1所示。

图1 矩形永磁体Fig.1 Rectangular permanent magnet
此外,永磁同步电主轴的结构模型和结构参数分别如图2和表1所示。
文中所有的分析都是借助于Ansys软件和Matlab软件进行。计算域是由电机的一个横截面来代表,图3也呈现了有限元网格转子转动被认为是“压缩”被放置在电机气隙中的空气[11]。为了达到良好的数值精度,该区域的网格进行了彻底的细化,如图3所示。

1.永磁体 2.定子 3.转子 4.轴 5.气隙图2 永磁同步电主轴的结构模型Fig.2 Structure model of permanent magnet synchronous electric spindle

极数16气隙长度/mm16槽数36相数3永磁体材料钕铁硼定子外径/mm181定子内径/mm519磁体厚度/mm4转子外径/mm463额定转速/r·min-12000
图3 计算域和有限元网格Fig.3 Computational domain and finite element mesh
在所有研究的情况下,定子槽的数目和转子磁极的数目都是一样的。对于转子的不同位置通过仿真对定子绕组不加电流的电机获得齿槽转矩。对于每次转子的位置,模型网格会自动被计算。
3 有限元仿真
3.1 梯形磁体对永磁同步电主轴齿槽转矩的影响
在梯形磁体的情况下,包括两种模型:(1)梯形磁体的长底边与转子外表面接触;(2)梯形磁体的短底边与转子外表面接触,如图4所示。

(a) 梯形长底边与转子接触 (b) 梯形短底边与转子接触图4 梯形磁体的结构Fig.4 Structure of trapezoidal magnet
在所有的情况下,磁体的厚度与矩形磁体的厚度是相同的(hm=4 mm)。同时,梯形长底边的长度与矩形长边的长度是一样的。梯形磁体长底边的角度β被当做成一个参数,这个参数将会反应相比于梯形的长底边梯形的短底边的减少。
图5显示的是梯形长底边与转子外表面接触时,随着β的变化,齿槽转矩的最大值与矩形磁体时齿槽转矩的最大值的比值和基波幅值与矩形磁体时基波幅值的比值。
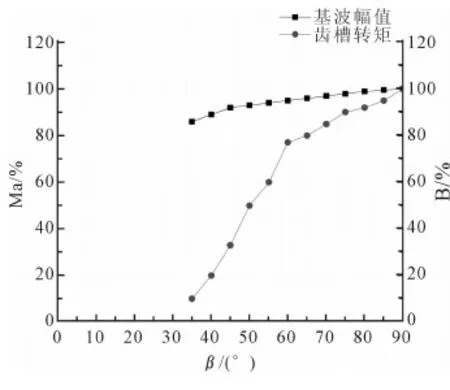
图5 长边与外表面接触时齿槽转矩值和基波幅值的对比图Fig.1 Comparison of cogging torque value and fundamental amplitude value when long bottom contact with the outer surface
通过图5可以看出当β=35°时,与矩形磁体相比,齿槽转矩的最大值下降了90%。在同一条件下,基波的幅值下降要慢一些,大约下降了14%。
图6显示的是梯形磁体短底边与转子外表面接触时的结果。

图6 短边与外表面接触时齿槽转矩值和基波幅值对比图Fig.6 Comparison of cogging torque value and fundamental amplitude value when short bottom magnet contact with the outer surface
与图5相比,齿槽转矩下降的缓慢一些,而基波幅值的下降更缓慢。因此。梯形磁体对降低齿槽转矩的最大值有快速的影响,但对降低基波幅值有很缓慢的影响。
3.2 阶梯磁体对永磁同步电主轴齿槽转矩的影响
改变阶梯磁体每阶的高度(h1),磁体的尺寸由参数h1和h2代表,如图7所示。所有的磁体变形都与最初的矩形磁体相比较。所分析的阶梯磁体中H1和H2与原来的矩形磁体一样。
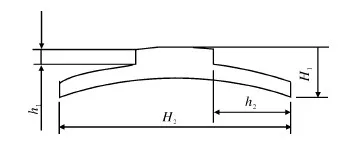
图7 阶梯磁体的结构Fig.7 Structure of ladder magnet
图8显示的是以下条件下的结果:磁体的厚度是H1,步的宽度是常数,即h2=0.25H2,只变化阶梯磁体中第一阶梯的高度h1。

图8 当h2=0.25H2时阶梯磁体的齿槽转矩值和基波幅值对比图Fig.8 Comparison of cogging torque value and fundamental amplitude value of ladder magnet as h2=0.25H2
从图8可以明显的看出当h1=1 mm时,齿槽转矩的最大值与矩形磁体相比减少了98%,而此时基波幅值仅减少了8%。而当h1=3 mm时,基波幅值与矩形磁体时相比减少了22%,但此时齿槽转矩就减少了39%。
4 结论
本文提出两种永磁体结构来降低永磁同步电主轴齿槽转矩的最大值和基波幅值,这两种永磁体结构分别是梯形磁体和阶梯磁体。
通过运用Ansys对这两种永磁体结构的永磁同步电主轴进行仿真,并用matlab对仿真的数据进行分析且与原永磁同步电主轴(矩形磁体)进行对比,得出以下结论:
(1)应用梯形磁体结构,在梯形磁体长底边与转子外表面接触情况下,当β=35°时,齿槽转矩的最大值与原来的矩形磁体相比减少了90%,而基波幅值仅减少了14%。
(2)应用梯形磁体结构,在梯形磁体短底边与转子外表面接触情况下,当β=35°时,齿槽转矩的最大值与原来的矩形磁体相比减少了63%,而基波幅值减少了8%。
(3)应用梯形磁体结构,最好选用梯形磁体长底边与转子外表面接触这种模型。当在保证平均转矩等运行性能的前提下,β角值越小越好即齿槽转矩的最大值和基波幅值都会随着β的值减小而减小。
(4)应用阶梯磁体结构,当h1=1 mm时,齿槽转矩的最大值与矩形磁体相比减少了98%,而基波幅值降低了8%。
[1] Liu T, Huang S, Gao J. A method for reducing cogging torque by magnet shifting in permanent magnet machines[C]// Electrical Machines and Systems (ICEMS), 2010 International Conference on. IEEE, 2010:1073-1076.
[2] Puscasu S V, Melcescu L, Covrig M. Cogging torque investigation in permanent magnet synchronous motor used for electrical vehicles[C]// Advanced Topics in Electrical Engineering (ATEE), 2013 8th International Symposium on. IEEE, 2013:1-4.
[3] Zhu Z Q, Ruangsinchaiwanich S, Howe D. Synthesis of Cogging-Torque Waveform From Analysis of a Single Stator Slot[J]. IEEE Trans Ia, 2006, 42(3):650-657.
[4] Yang Y, Wang X, Leng X, et al. Reducing Cogging Torque in Surface-mounted Permanent Magnet Motors by Teeth Notching[C]// Industrial Electronics and Applications, 2007. ICIEA 2007. 2nd IEEE Conference on. IEEE, 2007:265-268.
[5] 王晨, 曹光华, 陈栋. 一种削弱内置式永磁电动机齿槽转矩的新方法[J]. 微特电机, 2015, 43(1):9-12.
[6] 王道涵, 王秀和, 丁婷婷,等. 基于磁极不对称角度优化的内置式永磁无刷直流电动机齿槽转矩削弱方法[J]. 中国电机工程学报, 2008(9):66-70.
[7] Islam R, Husain I, Fardoun A, et al. Permanent-Magnet Synchronous Motor Magnet Designs With Skewing for Torque Ripple and Cogging Torque Reduction[J]. IEEE Transactions on Industry Applications, 2009, 45(1):152-160.
[8] Gu?emes, J.A, Iraolagoitia, A.A, Del Hoyo, J.J, et al. Torque Analysis in Permanent-Magnet Synchronous Motors: A Comparative Study[J]. IEEE Transactions on Energy Conversion, 2011, 26(1):55-63.
[9] Abdollahi S E, Vaez-Zadeh S. Reducing Cogging Torque in Flux Switching Motors With Segmented Rotor[J]. IEEE Transactions on Magnetics, 2013, 49(10):5304-5309.
[10]Bianchini C, Immovilli F, Lorenzani E, et al. Review of Design Solutions for Internal Permanent-Magnet Machines Cogging Torque Reduction[J]. IEEE Transactions on Magnetics, 2012, 48(10):2685-2693.
[11]Uncuta S, Melcescu L, Covrig M, et al. Numerical analysis of a PM synchronous motor used in electrical vehicles[J]. International Symposium on Advanced Topics in Electrical Engineering, 2011:1-6.
Analysis of cogging torque of permanent magnet synchronous electrical spindle
ZHONG Shuang-shuang, YU Shen-bo
(School of Mechanical Engineering, Shenyang University of Technology, Shenyang 110870, China)
Permanent magnet synchronous electrical spindle (PMSES) is widely used in variety high-performance speed and position control systems. In order to ensure the high quality of the operation, cogging torque should be reduced. According to the producing causes and the reducing methods of cogging torque, this paper presents two kinds of permanent magnet structure, which are trapezoidal magnet and steps magnet. The effects of the two methods on cogging torque of PMSES are investigated. Then, the PMSES of two kinds of permanent magnet structure is simulated by Ansys. At last, the data of the simulation is calculated, analyzed and compared by using Matlab. The results show that the suitable tilt angle of trapezoidal magnet and the suitable ladder height of steps magnet can reduce the maximum cogging torque value and the value of the amplitude of fundamental harmonic under the condition of no affecting running performance of the PMSES, such as average torque.
permanent magnet synchronous electrical spindle (PMSES); cogging torque; trapezoidal magnet; steps magnet
2016-02-25;
2016-04-13
国家自然科学基金资助项目(51175350),沈阳市科技计划项目(F15-199-1-13)。
钟双双(1991-),女,辽宁大连人,沈阳工业大学机械工程学院在读博士,研究领域为电主轴的振动与噪声。
TM351
A
1001-196X(2016)04-0025-05
