HGM准双曲面齿轮小轮控制参数的确定

杨 林，明希军

(沈阳工业大学 机械工程学院，辽宁 沈阳 110020)

HGM准双曲面齿轮小轮控制参数的确定

杨 林，明希军

(沈阳工业大学 机械工程学院，辽宁 沈阳 110020)

为了得到最终的HGM小轮控制参数，从齿面修正的数学模型出发，利用基于Matlab 环境编写的TCA(Tooth Contact Analysis)程序，通过不断调整程序中的小轮控制参数初值，获得较为理想的齿面接触区域图和传动误差图。结果表明，该方法在确定小轮控制参数方面具有很好的效果。

HGM；TCA；齿面修正；小轮控制参数

0 前言

准双曲面齿轮用来传递两交错轴间的运动，具有承载能力强、传动平稳等优点，在汽车工业中得到广泛应用[1]。齿轮副的啮合质量是通过正确的切齿计算和小轮控制参数的调整来实现的。传统的方法主要是在齿面涂红丹粉法，但该过程比较繁杂，工作效率低下。目前比较常用的是TCA法，该方法可以在切齿前，确定小齿轮的控制参数，具有更高的效率[2]。

对切齿计算和齿面接触分析，吴序堂等[3]对准双曲面齿轮切齿方法做了理论研究,郑昌启[4]、毛世民[5]等推导了齿面接触分析方法，王小椿[6]等对螺旋锥齿轮齿面测量和机床加工参数的修正做了研究，Simon[7]对在数控机床上加工准双曲面齿轮做了研究，等。但利用TCA方法确定最终的小轮控制参数这一过程，少有论文进行论述。因此，本文从齿面修正的数学模型出发，利用基于Matlab 环境编写的TCA程序，通过观察分析齿面接触区域图和传动误差图，在程序中调整相关参数，最终确定小轮控制参数。

1 齿面修正的数学模型的建立

1.1 小轮理论齿面与实际齿面间的距离

图1、2中，用虚线表示小轮理论齿面s(1)，用实线表示小轮实际齿面s(2)。

图1 小轮理论齿面与实际齿面Fig.1 Theoretical and actual tooth surface of the pinion

图2 理论齿面与实际齿面间的距离Fig.2 Distance between theoretical and actual tooth surface

如图2所示，齿面s(1)、s(2)间的距离在M0点附近可近似为

1.2 齿面修正的数学模型

Gleason公司实验得出：当两齿面间的距离Δδ≤0.006 35 mm时，用红丹粉可以检测出接触印痕。用这个原则来修正理论齿面曲率，得到实际曲面曲率。

Δkn=0.0508/l2

(1)

若α是齿长方向，如图3所示，齿面长度近似为b/cosβ，接触区长度为fb/cosβ,f为接触区长度与齿面长度之比。由式(1)可得齿长方向的诱导曲率修正值为

修正值符号的选取要使小轮凸面的齿长曲率增大，小轮凹面的齿长曲率减小。

图3 接触区长度计算图Fig.3 Schematic diagram of bearing length

若α是齿高方向，曲率修正是按接触区宽度为齿高一半来进行的，即

式中，fh≈4。

由式(1)可得齿高方向的法曲率修正值为

引入齿高曲率修正系数Kp，则

修正值符号的选取要考虑到齿高曲率在小轮凹凸面符号相反。

综上可知，改变f和Kp的值，可实现对齿面接触区域进行修正。加长接触区时，应加大f的值，反之，应减小f的值；接触区变宽时，应减少Kp的值，反之，应加大Kp的值。一般情况下，当小轮螺旋角β1≥20°时，Kp=0，β1=25.92°，故只对齿长接触系数f进行TCA验证。

2 齿轮副TCA模型建立

2.1 TCA分析的基本思想

大轮和修正后的小轮的传动属于点接触共轭齿面传动，接触点的集合为一条接触轨迹线。不发生曲率干涉的情况下，在每个接触点都可以确定一个接触椭圆，接触椭圆的集合构成了齿面接触区域。通过在TCA分析程序中调整小轮的控制参数，来调整接触区域的大小、形状和位置，获得较为理想接触区域和传动误差，确定小轮的控制参数。

2.2 建立齿面接触区

大轮坐标系S2中，大轮齿面方程记为r2、n2、t2；小轮坐标系S1中，小轮齿面方程记为r1、n1、t1。小轮装配到S2中，如图4、5所示。

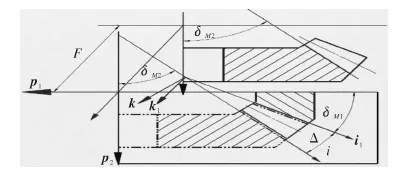
图4 齿轮副装配Fig.4 Assembly gear-pair

图5 有安装误差的齿轮副装配Fig.5 Assembly gear-pair with installation error

R2=O2O1+R1

(2)

如图6所示，H、V、J可表示为

H=-(O2O1,p2,j)

V=-E+O2O1·j

J=-(O2O1,p1,j)

进行TCA分析时，首先在大轮齿面上指定一点M，作为分析的起点。此点满足

(3)

用牛顿法，可求出P点处的Δq2和θ2。把Δq2和θ2代入方程组(2)，用拟牛顿法解出Δq1和θ1。再由Δq1、Δq2、θ1、θ2求出R1、R2、O2O1和V、H的值。然后在此安装条件下，选一个适当的步长i，令Δq2=Δq2+i，q2=q20+Δq2，代入方程组(3)，求出新的接触点，并检查是否超出边界，若超出，程序返回到第一个接触点，令Δq2=Δq2-i，反向找新的接触点，一直到超出边界为止。这样大轮齿面上的轨迹点就求出来了。再利用微分几何知识和Δδ=0.006 35 mm，即可得出齿面接触区。

2.3 建立传动误差函数

小轮、大轮从机床调整位置旋转到第一个指定接触点，转过的角度分别为ε10和ε20，转到啮合位置为ε1和ε2。则传动误差函数为Δε=(ε1-ε10)-z1/z2·(ε2-ε20)。

3 确定小轮控制参数的实现

轮坯设计参数和部分加工参数作为程序初值，如表1和表2所示。用变性法加工小轮时，小轮控制参数有八项，下面选取刀盘齿形角a01、垂直轮位修正量EMx、齿长接触系数修正量fx和产形轮锥距修正量R01X为例，进行说明确定小轮控制参数的过程。在TCA程序中的相应表达式为：

表1 准双曲面齿轮轮坯设计参数

表2 准双曲面齿轮部分加工调整参数

(1) disp(′垂直轮位为:′)

E01=E+E02+EMx；

(2) disp(′齿长接触系数:′)

m=d2/z2;

ifm>=8f=0.25+fxelsef=0.3+fxend

(3)disp(′产形轮节锥距初值为:′)

R011=Rf1tan(af1)/(tann+tan(af1))+R01X

图6 选定小轮刀盘齿形角a01Fig.6 The pinion cutter tooth profile angle a01

图6中，观察齿面接触区域可知，当a01取不同的值时，其形状、大小和位置也不同：图6a，接触轨迹向内端严重弯曲；图6b, 齿根无接触区域，但齿顶接触区较为理想，为调整其他小轮控制参数创造了条件; 图6c, 中部接触区图形，每个瞬时椭圆长轴大小不一致。观察各传动误差图：图6a、 6b中曲线不重叠不相交，这时只能由轮齿齿顶强制传递，产生边缘接触；图6c曲线重叠且相交，第一条曲线与另外两条相交，说明重叠系数大，有三个轮齿同时参与啮合；此外，图6b和6c图曲线弯曲程度相似，再结合图6b接触区，说明齿顶传动比较平稳。综上所述，a01=-31°比较合适。

确定EMx，当a01=-31°，其他小轮控制参数取0时，EMx取正值，TCA程序中解齿面方程组的部分，不收敛，分析中断；EMx取负值，情况相反，EMx取得越小，齿顶接触区越向内端倾斜，如图7所示。经比较，EMx=-3时，齿面接触区域图和传动误差图比较合适。

确定fx，当a01=-31°、EMx=-3，其他小轮控制参数取0时，fx由0调整到0.04，图8a中的接触区域与图7a相比，齿长方向的宽度有所增加，齿面修正的数学模型得到了验证。fx=0.08时，图8b中接触区域宽度变窄，说明增大fx时，宽度不会无限变宽，到达一定限度后，再增大fx宽度会变窄。

图7 选定垂直轮位修正量EMxFig.7 Vertical round correction EMx

图8 确定齿长接触系数修正量fxFig.8 Tooth contact coefficient correction fx

在图8b的小轮参数基础上调整R01X，当R01X取负值时，齿顶接触区域有向内端倾斜的趋势；当R01X取正值时，倾斜趋势相反，当R01X=0.25时，如图9所示。

图9 确定产形轮锥距修正量R01XFig.9 Shape cone distance correction R01X

按上述方法确定小轮控制参数虽稍显复杂，却相对有效，有规律可循。

4 结论

用TCA确定小轮控制的过程可以得出下面结论：(1)小轮刀盘齿形角a01主要影响菱形接触：|a01|减小，齿根接触区齿长方向的宽度会减小，齿顶接触区会增大；|a01|增大，情况正相反。(2)垂直轮位修正量EMx主要影响鱼尾形接触：接触轨迹向右弯曲时，对小轮凹面EMx取正值，对小轮凸面EMx取负值；接触轨迹向左弯曲时，EMx取值情况相反。(3)小轮产形轮节锥距R01X主要影响对角接触：接触轨迹外对角时，对小轮凹面R01X取负值，对小轮凸面R01X取正值；接触轨迹内对角时，R01X取值情况相反。

[1] 曾韬.螺旋锥齿轮设计与加工[M].哈尔滨：哈尔滨工业出版社，1989.

[2] 王星，方宗德，李声晋，等.HGT准双曲面齿轮传动的轮齿接触分析[J].西北工业大学学报，2014，32(3)：475-480.

[3] 樊红卫，谷霁红.螺旋锥齿轮设计与制造的研究现状与展望[J].机械制造，2009，47(540).

[4] 陈志新.共轭曲面原理[M].北京：科学出版社，1974-1977.

[5] 陈志新.共轭曲面原理基础[M].北京：科学出版社，1985.

[6] 陈惟荣.双自由度共轭曲面理论及其应用[J].机械工程学报，1981，4.

[7] 吴序堂.准双曲面齿轮啮合原理及其在刀倾半展成加工中的应用[J].西安交通大学学报，1981，15(1)：9-24.

[8] 吴序堂.格里森制准双曲面齿轮刀倾全展成切齿法的研究[J].机械工程学报，1985，21(2)：54-69.

[9] Litvin F L. A method of local synthesis of gears grounded on the connections between the principal and geodetic curvatures of surfaces [J].ASME Journal of Mechanical Design, 1981,103(1):114-125.

[10]郑昌启.弧齿锥齿轮和准双曲面齿轮的齿面分析计算原理[J].机械工程学报，1981，17(2)：1-12.

[11]毛世民，吴序堂.任意指定接触基准点的切齿理论[J].西安交通大学学报，1985，19(5)：1-10.

[12]Krenzer T J. Tooth contact analysis of spiral bevel and hypoid gears under load [N]. SAE Tech.Pap. ,No.810688, 1981.

[13]Krenzer T J, Knebelr R. Computer aided inspection of bevel and hypoid gears [N].SAE Tech.Pap.,No.831266,1983.

[14]王小椿，王军，姜红，等.螺旋锥齿轮的齿面测量及机床加工参数的修正[J].机械工程学报，2003，39(8)：124-128.

[15]Simon V V. Generation of Hypoid Gear on CNC Hypoid Generator [J].Journal of Mechanical Design, 2011, 133(12):1-9.

Determination of control parameters of the pinion for HGM hypoid bevel gear

YANG Lin，MING Xi-jun

(School of Mechanical Engineering, Shenyang University of Technology, Shenyang 110020，China)

To determine final control parameters of the pinion of HGM hypoid bevel gear, in this paper, through the mathematical model of tooth surface modification and TCA program (Tooth Contact Analysis) based on Matlab environment, continuously adjusting the initial values of the pinion control parameters, finally obtained desirable diagram of tooth surface contact area and driving error. The simulation results show that the method is effective in determination of the pinion control parameters.

HMG; TCA; tooth surface modification; control parameters of the pinion

2015-10-21；

2015-12-24

辽宁省沈阳市工业科技攻关项目(F15-040-2-00)

杨林(1960-)，男，沈阳工业大学教授。主要从事机械产品的设计研发，近年开始从事螺旋锥齿轮制造技术及装备的研究。

TH164;TH132.41

A

1001-196X(2016)04-0035-05