基于LS-DYNA台阶微差爆破最佳延期时间的降振控制

楼晓明, 周文海, 陈必港

(1. 福州大学紫金矿业学院， 福建 福州 350116； 2. 福州大学爆炸技术研究所， 福建 福州 350116)

基于LS-DYNA台阶微差爆破最佳延期时间的降振控制

楼晓明1, 2, 周文海1, 陈必港1

(1. 福州大学紫金矿业学院， 福建 福州 350116； 2. 福州大学爆炸技术研究所， 福建 福州 350116)

为探究不同延期时间对台阶爆破振动的影响， 在总结分析国内外有关研究基础上， 运用动力有限元软件LS-DYNA进行台阶微差爆破数值模拟. 爆破模型采用双孔柱状耦合装药的0、 17、 25、 42 ms四种不同延期时间起爆方式， 模拟过程中在临近爆破台阶的下个台阶面上选取3个监测点， 采集4种延期起爆合成速度时间曲线. 通过观测曲线发现， 当延期时间为25 ms时， 合成速度峰值最小、 降振最为明显； 而坡脚处峰值速度最大， 说明出现应力集中现象. 同时实地进行单孔爆破测振实验， 依据谷峰时速分布特征， 对某实测简单振动波进行Gaussian多峰拟合， 发现该振动波最小合成速度出现时间点为t=25 ms左右.

微差爆破； 爆破振动； 峰值速度； 多峰拟合

0 引言

露天微差爆破合理延期时间选取能够改善爆破质量、 减少炸药单耗、 提高岩石破碎率、 降低爆破振动、 增加经济效益[1]. 国内不少学者将动力有限元软件模拟分析引入微差时间选取研究， 取得了众多成果. 沈晓松等[2]通过Split-Desktop 3.0软件模拟微差爆破过程， 认为微差爆破产生振动的主要影响因素之一为延期时间， 通过不断改变延时大小， 结合最终模拟结果给出最佳降振延时为60 ms左右. 吴贤振等[3]将LS-DYNA用于微差爆破模型建立， 通过振动波叠加规律指出质点振动速度最小对应的微差延时为28 ms. 凌同华等[4-5]利用LS-DYNA和RSPWVD软件建立微差爆破模型， 通过小波变换时能密度分析， 将波段分层重构和分辨分解给出最佳降振延期控制时间.

通过上述有关微差爆破降振延时控制研究分析发现， 由于地质条件和爆破环境以及所选取的研究理论不同， 最终得出的延期时间差异较大. 本文利用有限元动力软件LS-DYNA对微差爆破全过程进行仿真模拟， 通过观测模拟过程中监测点速度曲线变化规律， 以期给出最佳降振控制时间； 同时采用具体现场实验测振， 对测振波峰值速度进行时程分析， 得出最佳降振时间， 为今后微差爆破降振研究提供实践指导.

1 材料模型

根据露天矿逐孔台阶微差爆破实际情况建立三维台阶模型作为研究对象， 模型采用cm-g-μs国际单位制， 台阶高度取12 m， 坡面角70°， 台阶纵向布置两个炮孔， 第一个炮孔距坡顶线距离取3 m， 排间距6 m. 两炮孔参数相同， 孔径150 mm， 孔深14.5 m， 堵塞长度4 m， 装药长度10.5 m， 采用耦合装药， 单孔药量取192 kg. 模型整体规格参照文献[6]研究， 坡脚距左边水平距离10 m， 坡顶线距右边距离16 m， 上下边界距离大概为坡高2倍. 为研究方便以及能清晰观测爆破过程中各物理量的变化情况， 模型厚度取炮孔直径， 即150 mm. 模型具体尺寸如图1所示.

1.1 岩石材料及模型

岩石材料选取典型的弹塑性石材花岗岩作为研究对象. 建模时岩石材料采用MATPLASTICKINEMATIC模型. 过程中需要岩石各物理参数和力学参数， 故参考《水利水电工程岩石试验规程(SL264-2001)》[7]实体采样， 对12组花岗岩岩心进行力学测量， 分别计算出岩心密度(ρ)、 泊松比(μ)、 杨氏模量(E)、 屈服应力(σy )、 切线模量(Etan)、强化系数(β)等, 然后对12组数据取平均值作为最终取值. 具体参数如表1所示.

表1 岩石主要物理力学参数表Tab.1 Physical and mechanical parameters of rock

1.2 炸药材料及模型

炸药选取2#岩石乳化炸药， 其材料类型为： HIGHEXPLOSIVEBURN. 炸药状态方程选取通常有两种， 一种是含炸药产物成分的BKW或者KHT方程， 另一种是不含炸药产物的JWL方程， 由于炸药产物对延期控制研究影响甚微， 所以选取JWL状态方程. 具体材料参数及状态方程参数如表2所示.

表2 炸药主要参数表Tab.2 Parameters of explosive

炸药爆炸时状态可用等熵JWL方程表示为：

(1)

爆炸过程中时间极短， 可假设与周围没有热交换， 也就是说是一种等嫡绝热过程， 故在等嫡绝热条件下， 比内能增量可表示为：

(2)

结合式(1)、 (2)， 对结果积分可得：

(3)

结合式(1)、 (3)， 消除常数C可得最终炸药JWL状态方程为：

(4)

其中：A、B、R1、R2、ω为材料常数；p为压力；V为相对体积；E0为初始比内能.

1.3 堵塞物材料及模型

炮孔采用连续耦合装药， 孔口堵塞长度取4 m， 建模材料采用土壤和泡沫， 即： MATSOILANDFOAM. 具体模型参数可根据文献[8]研究结论选取， 其数值如表3所示.

表3 堵塞物模型参数表Tab.3 Model parameters of stemming

2 LS-DYNA建模和算法

利用动力有限元软件LS-DYNA建立由岩石、 炸药、 堵塞物三者组成的三维材料模型. 模型网格采用15 cm单元划分， 三维台阶顶部和前后三个面为自由面不施加约束， 其他三个面统一定义为透射边界(无反射边界条件)， 岩体采用Lagrange算法， 炸药和堵塞物采用ALE流体类型定义. 因为Lagrange网格会随着爆破过程的发展而发生材料变形， 一旦发生较大变形就会对后期计算带来困难； 而ALE算法会随材料变形重购网格， 增大了材料的稳定性. 炮孔内物质变形较大， 所以采用ALE算法定义网格.

欧拉法、 Lagrange法以及ALE算法位置导数可表示为：

(5)

其中：vi表示X质点速度；ωi表示选取标准参考位置ξ的速度.

ALE力学方程可用流体运动方程来表示， 将式(5)流体力学方程转化为ALE控制方程为：

(6)

(7)

(8)

结合式(4)、 (6)、 (7)、 (8)组成封闭方程组对整个模型实施运算.

3 动力有限元求解结果

李夕兵等[5]对爆破振动波传播过程中能量突变点的质点进行信号分析， 将振动波分层重构和分辨分解后的小同频带波段速度随时间有较大变化的特点作为最佳延时控制判断依据， 发现合成速度波段峰值可作为爆破降振指标； 娄建武等[9]同样提出可以基于速度峰值理论为出发点确定最佳微差时间来改善振动危害和降低爆破振动.

依据《爆破安全规程》[10]和国内外研究成果， 考虑实际工程情况， 选取高精度雷管微差时间为标准. 模型两炮孔间延期时间分别取0、 17、 25、 42 ms四组进行数值模型分析. 模拟过程中在台阶模型紧接炮孔平台的下一个台阶面上选取3个监测点， 分别为块体4551、 2601、 574， 记作监测点A、B、C， 具体见图2. 对整个爆破过程中3监测点合成速度-时间变化数据采集， 四组不同延期时间对应三轴合成速度云图见图3～6， 对应的时速分布特征曲线见图7～10.

从图7～10可知， 两相邻炮孔延期时间取0、 17、 25、 42 ms时， 监测点A峰值速度分别为： 18.7、 11.1、 10.4、 10.8 cm·s-1； 监测点B峰值速度分别为： 16.9、 8.42、 8.31、 8.69 cm·s-1； 监测点C峰值速度分别为： 14.5、 6.51、 6.19、 7.43 cm·s-1. 故随着延期时间递增， 合成速度呈递减趋势； 当速度递减到一定程度， 随着延期时间的递增， 合成速度出现增大趋势； 直到爆破后期， 能量逐渐衰减， 合成速度再次出现递减. 通过此次模拟发现， 炮孔延期时间为25 ms时， 三监测点峰值速度值均为最小， 降振效果最为明显.

4 工程实例

为获得简单、 叠加干扰较少的波形作为延期控制研究对象， 在紫金山某爆区附近实施试爆实验. 该爆区岩层较为破碎， 分化节理严重， 矿岩类型主要以花岗岩和蛇纹岩为主， 具体如图11所示. 实验过程采用Blast-UM型爆破测振仪对单孔起爆产生的地震波测振， 用最大爆破振动合成速度计算. 将获取的该波段三轴速度与对应时间数据导入Excel进行矢量合成， 得到合成速度数据， 将该数据导入Origin 9.0软件绘制出合成速度-时间曲线图. 由于该曲线由离散数据组成， 所以对该曲线进行快速傅里叶变换(FFT)， 再经过除噪(Denoise)、 平滑(Smooth)处理后便得到理想的合成速度-时间图， 如图12所示.

通过上述分析表明， 速度波段中主要的突变点(波峰、 波谷)可作为延期控制研究对象. 该速度波谷峰数据可作为降振研究载体. 为获取该波段谷峰主要信息， 对该波段采取多峰拟合， 整个过程选取Gaussian法进行数据处理. 其拟合的基本原理是最小方差原则， 将Gaussian参数调整和限定， 可得到各峰值高度、 宽度、 峰区面积、 峰中心位置以及对应时间等重要信息. 本文只对该波段波谷进行拟合， 由于诸多隐峰的存在， 所以拟合关键步骤为寻峰， 其信息具体见表4和表5所示. 图13为该速度波段波谷分布状态(横坐标代表时间； 纵坐标代表波幅)， 图14为拟合后三轴合成速度曲线.

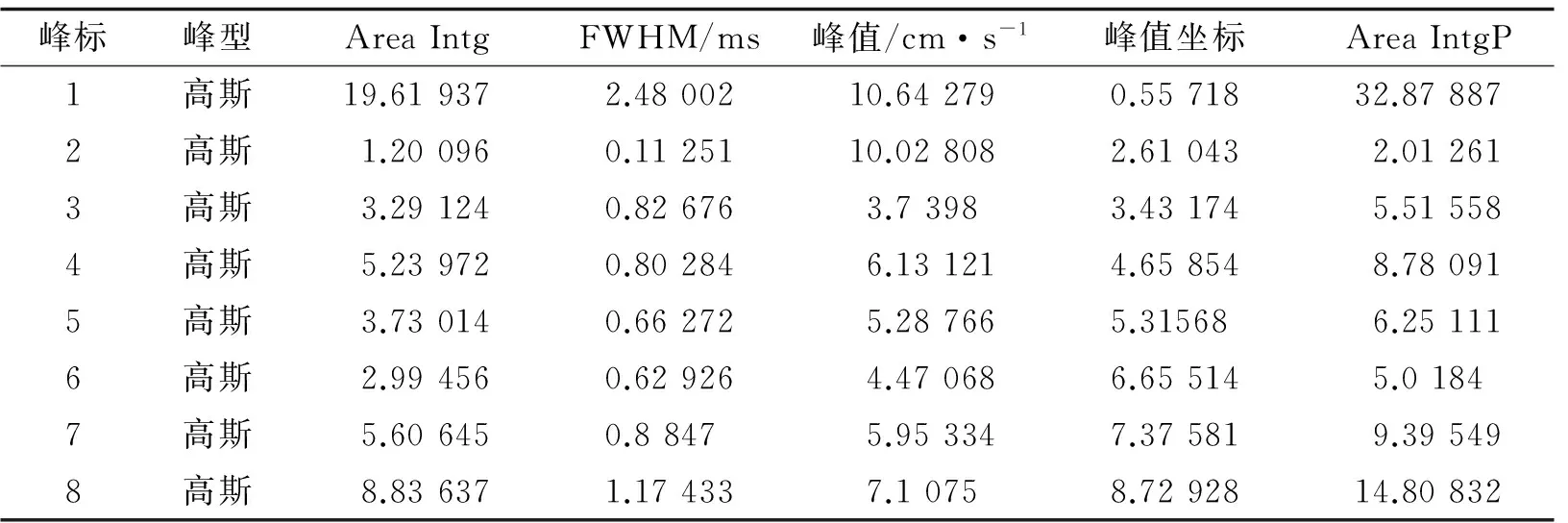
峰标峰型AreaIntgFWHM/ms峰值/cm·s-1峰值坐标AreaIntgP1高斯19.619372.4800210.642790.5571832.878872高斯1.200960.1125110.028082.610432.012613高斯3.291240.826763.73983.431745.515584高斯5.239720.802846.131214.658548.780915高斯3.730140.662725.287665.315686.251116高斯2.994560.629264.470686.655145.01847高斯5.606450.88475.953347.375819.395498高斯8.836371.174337.10758.7292814.80832

表5 峰值时间-速度方差表Tab.5 The peak time and velocity variance table

波谷拟合报表显示， 相关系数Adj.R-square=0.975 56(接近1)， 表明数据相关性较好， 能够有效反应振动波质点的离散程度； 卡方系数Reduced Chi-Sqr=0.136 32(趋近0)， 同样表明拟合值与实际值之间偏差程度尚可接受， 故可用此次最小峰值拟合作为研究样本. 通过图14最小峰值拟合曲线观察发现， 多峰拟合积累曲线突出集中处对应时间点为t=25 ms左右， 所以根据合成速度积分理论可知， 该处振动位移最小， 可作为爆破振动最小时间点.

5 结语

1) 通过模拟发现， 微差爆破过程中振动波合成速度随延期时间的递增， 出现先递减后递增， 最后快速递减规律.

2) 通过三个监测点合成速度变化规律发现， 四种不同延时起爆方式中，A监测点峰值速度明显高于其他监测点， 说明起爆过程中坡脚位置出现应力集中现象， 导致爆破振动增大.

3) 通过现场单孔试爆测振实验发现， 振动波合成速度出现最小值时间点为25 ms左右. 说明现场实验所得最佳降振时间与数值模拟结果基本吻合， 该时间点可作为台阶微差爆破降振的最佳延期时间， 并且此次模拟过程与辅助实验具有普遍性， 其结果可为常规台阶微差爆破降振研究提供技术参考.

[1] ZHENG J J, LOU X M, LUO D P. Vibration superposition in tunnel blasting with millisecond delay[J]. Journal of Southwest Jiaotong University(English Edition), 2009,17(1): 42-46.

[2] 沈晓松, 赵明生, 池思安, 等. 微差时间对爆破块度影响的试验研究[J]. 爆破, 2012, 29 (3): 70-73.

[3] 吴贤振, 尹丽冰, 刘建伟, 等. 基于LS-DYNA的临近采空区多段爆破微差时间优化研究[J]. 爆破, 2015, 32(1): 87-92.

[4] ZHAO M S , ZHANG J H, YI C P. Time frequency analysis based on single-stage addition of wave forms of blasting vibration signals[J]. Journal of China Coal Society, 2010, 35(8): 1 279-1 282.

[5] 凌同华， 李夕兵. 基于小波变换的时-能分布确定微差爆破的实际延迟时间[J]. 岩石力学与工程学报, 2003, 23(13): 2 266-2 270.

[6] MA G W, AN X M. Numerical simulation of blasting-induced rock fractures[J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(6): 966-975.

[7] 长江水利委员会长江科学院. 水利水电工程岩石试验规程： SL 264-2001[S]. 北京： 中国水利水电出版社, 2001.

[8] YANG R, BAWDEN W F, KATSABANIS P D. A new constitutive model for blast damage[J]. International Journal of Rock Mechanics and Mining Science. 1996, 33(3): 245-254.

[9] 娄建武, 徐全军, 龙源. 影响核岛新浇混凝土强度的爆破振动速度阂值研究[J]. 世界地震工程, 2003, 19(2): 163-167.

[10] 中华人民共和国国家质量监督检验检疫总局， 中国国家标准化管理委员会. 爆破安全规程： GB6722-2014[S]. 北京： 中国标准出版社, 2014.

(责任编辑： 蒋培玉)

Vibration reduction study of step millisecond blasting of optimal time delay control based on LS-DYNA

LOU Xiaoming1, 2， ZHOU Wenhai1， CHEN Bigang1

(1.College of Zijin Mining， Fuzhou University， Fuzhou, Fujian 350116， China；2. Institute for Explosive Technology， Fuzhou University， Fuzhou, Fujian 350116， China)

In order to study the impact of different delay time on vibration of bench blasting, the dynamic finite element software LS-DYNA was applied in numerical simulation. The four ways of initiating, whose delay time are 0 ms, 17 ms, 25 ms and 42 ms respectively, were adopted in two blast holes model. During the simulating process, three monitoring points were selected on the bottom stage, from where four kinds of synthetic velocity - time curves are formed. These curves show that peaking velocity is bottom at 25 ms with a minimum vibration, while the stress concentration emerges at slope. By contrast, after vibration measurement of single hole blasting and Gaussian multi-peaks fitting for this vibration, the minimum synthetic velocity of this vibration is around 25 ms.

millisecond blasting； blasting vibration； peak velocity； multi-peaks fitting

10.7631/issn.1000-2243.2016.05.0753

1000-2243(2016)05-0753-07

2015-06-09

楼晓明(1972-)， 博士， 副教授. 主要从事工程爆破研究, 331261323@qq.com

国家自然科学基金资助项目(41072232)； 福建省自然科学基金资助项目(2011J01310)

TD235.1

A