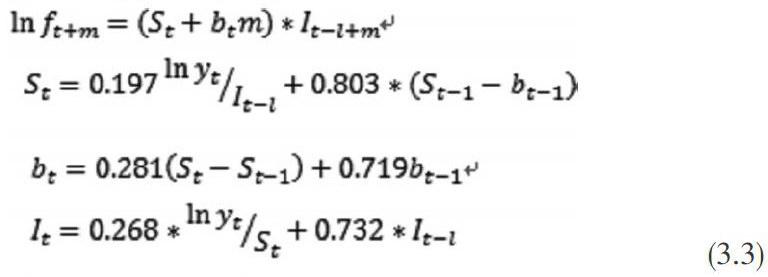基于财务数据的电网公司购售电预测建模研究

周振

摘要：购售电指标是影响电网企业经济效益的重要指标，对购售电量、收入、现金流等的科学预测是保证电网企业财务预算准确性的重要前提。本文从国网公司、省电网公司、市电网公司购售电情况三方面对电网企业财务数据进行分析，分别采用指数平滑法、灰色模型法、回归分析法，建立预测模型，通过对比分析实际与预测值的差异，得出有效的预测模型。

关键词：购售电预测 回归分析 指数平滑预测模型

购售电量、电费、现金流预测是电网公司损益预算编制、现金流预算编制、经营预测的起点，是投资能力测算、工程项目可研财务评价、工程项目财务后评价等最关键的参数。如何提高购售电预测准确性，是保证财务预算准确性的重要前提。目前国网财务系统中存储了大量的购售电相关数据，却由于财务部门缺乏成熟的购售电预测模型，无法做出精确的电量预测，对业务部门提供的电量预测数据的准确性没有发言权，只能被动接受。本文通过搭建购售电综合预测模型，一方面期望可以有效提升购售电预测的精准度，改变财务部门被动接受业务部门所提供的购售电预测数据的现状，另一方面为公司开展经营预测和工程项目经济效益评价夯实基础。

一、建模原理

（一）回归分析法

回归分析是一种应用极为广泛的数量分析方法。利用数据统计原理，对大量统计数据进行数学处理，并确定因变量与自变量的相关关系，建立一个相关性较好的回归方程（函数表达式），并加以外推，用于预测今后的因变量的变化的分析方法。回归分析主要解决以下方面的问题：一是确定变量之间是否存在相关关系，若存在，则找出数学表达式；二是根据一个或几个变量的值，预测或控制另一个或几个变量的值，且要估计这种控制或预测可以达到何种精确度。该方法一般用于年度预测。

（二）灰色模型法

灰色模型（grey models）是通过少量的、不完全的信息，建立灰色微分预测模型，对事物发展规律作出模糊性的长期描述的方法。其基本思想是用原始数据组成原始序列（0），经累加生成法生成序列（1），它可以弱化原始数据的随机性，使其呈现出较为明显的特征规律。对生成变换后的序列（1） 建立微分方程型的模型即GM模型。用GM模型进行预测，精度较高的仅仅是原点数据以后的1到2个数据，即预测时刻越远预测的意义越弱。

原始数据列：X（0）=（X（0）（1），X（0）（2），…X（0）（n）），n为数据个数。

（1）原始数据累加，弱化波动性和随机性

（2）累加生成数据做均值生成矩阵A，B

（3）灰色模型的参数分别为a，b

（4）计算得到拟合值

（5）对拟合值进行离散，得到预测值

（三）指数平滑法

指数平滑法认为时间序列的态势具有稳定性或规则性，所以时间序列可被合理地顺势推延。指数平滑法有助于预测存在趋势和季节性的序列。根据平滑次数不同，指数平滑法分为：一次指数平滑法、二次指数平滑法和三次指数平滑法等。由于月度与季度购售电具有季节性，本文主要使用三次指数平滑法中的Winters乘法模型，并借助于spss软件进行数据建模分析。

二、建模应用

本节从国网公司售电量、省电网公司、市电网公司购售电三个方面对建模方法进行应用与分析，并对模型进行验证。

（一）回归分析方法在国网公司购售电预测建模中的应用

由于售电量与宏观经济的变动等因素具有高度的相关性，因此本文使用国网年度售电量与GDP进行相关关系分析并建立模型。具体测算方法为：使用2003-2013年数据，建立年度售电量与GDP的相关关系模型，由同期的GDP计算得到售电量预测值。

建立年度售电量与GDP回归模型，模型拟合度为0.993，拟合图如图3.1所示，建立模型为：

lnY=ln0.939+0.795lnX （3.1）

其中Y为售电量，X为GDP。

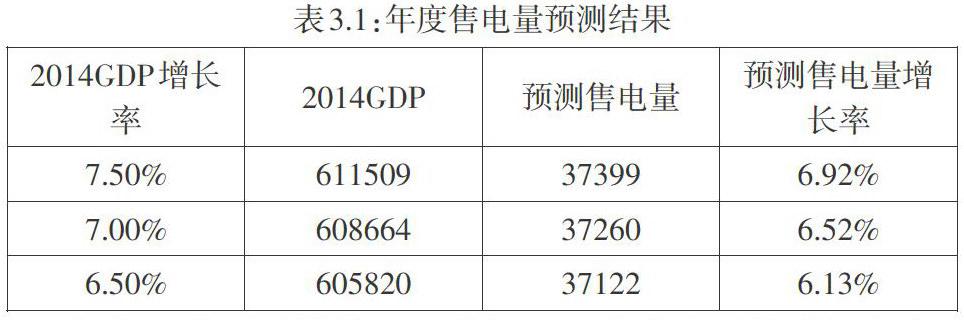
由回归模型计算得到年度售电量预测值，具体结果见表3.1，当GDP增长率为7.5%时，预测2014年售电量为37399亿千瓦时，电量增长率为6.92%；当GDP增长率为7%时，预测售电量为37260亿千瓦时，电量增长率为6.52%；当GDP增长率为6.5%时，预测售电量为37122亿千瓦时，电量增长率为6.13%。

由表3.1的预测结果可以看出，2014年售电量的增长率约为6.52%，这一结果与目前售电情况来看较为相符，说明建模效果较好，预测模型可用。

（二）灰色模型与指数平滑法在省级电网公司购售电预测建模中的应用

本节以XX省电力公司为例对省电网公司售电收入与售电现金流进行分析，使用灰色模型法对售电收入进行分析，预测月度售电收入；使用回归分析法建立现金流入与售电收入模型。

1、灰色模型预测省售电网公司电收入

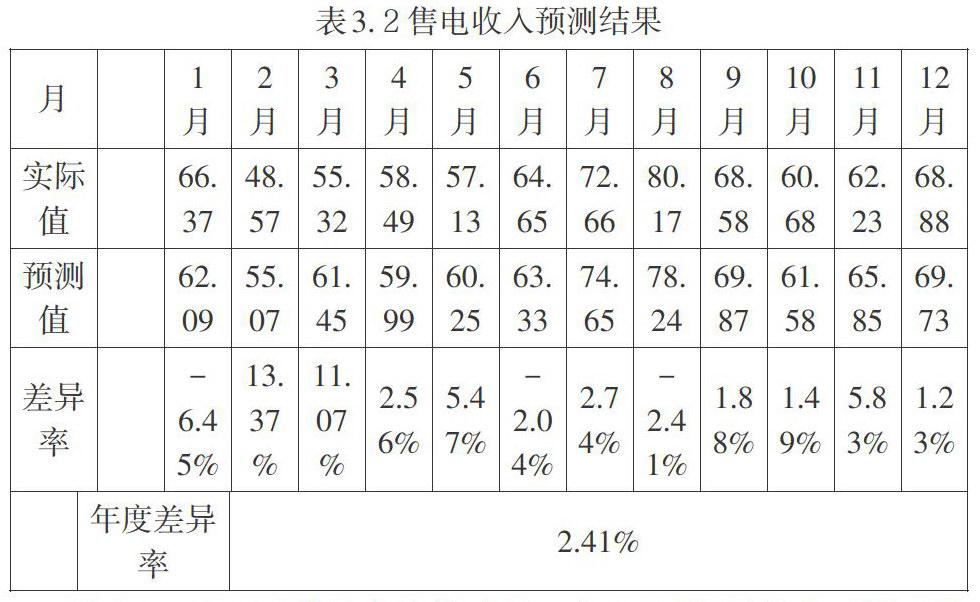
由于月度数据具有季节性，因此运用灰色模型结合季节分解法对数据进行建模分析。以2008年1月-2012年12月售电收入为原始数据，建立时间序列模型，预测2013年1-12月售电收入，模型预测结果见表3.2。

从表3.2的预测结果来看，除去前三个月预测差异较大，剩余月份预测结果与实际差异相对较小，整个年度的预测差异率为2.41%。前三个月由于春节原因的影响，故而差异较大。从预测结果看，灰色模型适合作特定月份的预测，亦可作为年度售电收入预测。模型建模的效果相对较好，预测模型可用。

2、回归分析法预测省电网公司现金流入

高质量的决策必须依赖于高质量的数据，由于有些数据存在异常，需要对其处理后再进行分析。本节对异常数据直接剔除。剔除异常数据后，建立本月含税售电收入与本月售电现金流入的回归模型，模型拟合度为0.913，模型显著性较好，模型拟合图如图3.2，建立幂函数方程：

Y=1.623*X0.889（3.2）

其中X为售电收入，Y为售电现金流入。

根据模型，使用当月的售电收入值预测售电现金流入值。因为当月的售电收入同样为未知数，因此还需要对当月的售电收入进行预测。可使用灰色季节性模型，指数平滑法等方法进行预测。本文只是给出一种建模思路，没有进行具体的测算。

对购电量的预测使用上述建模方法，得出预测差异率较大，建模效果不好。购电量的预测值可以使用售电量预测值扣除平均线损得到。

（三）指数平滑法与回归方法在市级电网公司购售电预测建模中的应用

由于购售电量、售电收入、购电成本等数据变动遵循规律基本一致，因此本节仅对售电现金流数据进行分析。

1、指数平滑法预测现金流量

以XX区供电公司2009年1月-2013年12月售电现金流序列为原始数据，运用Winters乘法，建立时间序列模型，模型拟合度为0.917，模型显著性较好，建立模型为：

其中[ft+m]为预测值，m为超前期数，yt为原始数据，St为数据的水平平滑值，bt为数据的趋势平滑值，It为数据的季节调整因子，l为季节周期长度。

模型参数见表3.3，模型拟合图如图3.1，模型预测结果见表3.4。

由表3.4可以看出，除1、2月份预测差异率较大外，其余月份差异均较小。由于1、2月份受到春节因素的影响，故而预测结果存在一定的偏差。总体来看，模型建模的效果较好，预测模型可用。

2、回归分析法预测现金流量

售电现金流回归分析思路为：首先建立年度现金流与时间的回归模型，由回归模型得到年度现金预测值，然后确定预测年度月现金流占全年的比重，最后将年现金流预测值依据月现金流比重在各月之间分配，得到月度现金流预测值。

（1）以XX区供电公司2008-2013年年度售电现金流入数据为原始数据，建立与时间的回归模型，模型拟合度为0.991，模型显著性较好，模型为：

Y=4218.727X-99.862X2+14484.905（3.4）

其中X为期数，Y为售电现金流入。

由公式（3.4）计算可以得出，2014年售电现金流入预测值为39122.76。

（2）确定月现金流比重

分析2008-2013年各月占全年的比重，并对各年比重设置权重，越近年份分配的权重越大，其中2008-2013年权重分别为0.025、0.025、0.025、0.025、0.1、0.8。

月售电现金流权重乘以2014年售电现金流入预测值等于2014年月现金流入预测值，具体预测结果见表3.5。由表3.5可以看出预测差异率在3%以内，表明使用年度售电现金流回归方法预测全年现金流，按各月所占全年权重分配预测值方法预测效果较好，预测模型可用。

指数平滑法与回归方法在市电网公司购售电预测中，建立的模型对售电现金流的预测结果均较好，差异率较小。可以使用该模型对购售电数据进行预测。

三、结束语

本文从全国、省电网公司、市电网公司三个方面对购售电财务数据进行分析，分别采用回归分析法、灰色模型法、指数平滑法建立了预测模型，并取得了一定的研究成果。针对国网公司年度售电量进行分析，建立了GDP与售电量的回归模型，根据GDP的预计变动情况，实现售电量预测。针对省电网公司购售电数据，建立了售电收入与现金流的回归模型；建立购售电收入预测的灰色模型，得到月度售电收入预测值。针对市电网公司购售电数据，建立售电现金流入的Winters加法模型，预测月度售电现金流量；建立年度现金流与时间回归模型，并依据月现金流比重分配现金流预测值，得到月度预测值。几种模型在实际分析应用中，差异率均较小，模型的建立可以为后续国网购售电预测提供参考。同时，预测模型的建立，一方面可以对预测方法进一步优化完善，另一方面可以洞察购售电量、收入、现金流变动等的规律，提升国网总体收入、现金流预测的精准度，为预算编制和经营预测夯实基础。但目前模型在具体的应用中仍需要改进，模型预测值与实际值在个别月份里预测差异较大，提高模型预测精确性，研究新的预测方法是下一步的研究方向。

参考文献：

[1]潘小辉，刘丽萍，李扬.提高月度售电量预测精度的一种新方法[J].电力需求侧管理，2013

[2]刘秋华，陈洁，甘海庆.基于改进灰色模型的售电量预测分析[N].统计与信息论坛，2009

[3]张颖，孙秋柏，陈雪波等.指数平滑法在现金流预测中的应用[N].测试技术学报，2014

[4]吴杰，宋国堂，卢志刚，张鸿.基于偏最小二乘回归与比重法的月售电量预测[N].电力系统及其自动化学报，2008