基于CGSS2003数据关于住房影响因素的报告
2016-12-01卢亚宁
卢亚宁

【摘 要】目的:分析收入、教育水平、家庭总人口数对住房的影响,选取使用面积为自变量,探讨人口基本特征因素对住房状况的影响。方法:基于全国综合社会调查(CGSS)2003年的调查数据,并用SPSS18.0对引用数据进行回归分析和方差分析。结论:受教育程度越高,家庭住房面积相对越高;收入越高,家庭住房使用面积相对越高,并且随着家庭总人口数的增加,住房使用面积相对应增加。
【关键词】住房状况;影响因素;回归分析
住房是生活的基本需求,住房状况会对人们的生活、工作和健康等方面产生深远影响。住房状况受到了住房制度、地区自然环境、社会文化和家庭状况等多因素的影响,它反映了住户的居住质量,并影响个人身体健康和社会稳定。
随着市场化改革的逐步深入,我国贫富分化越发显著,家庭人均住房情况也随之出现较大差距。在当前社会中,很多因素对家庭住房产生了影响,本文就收入、教育水平以及家庭总人口数进行了分析。
一、数据来源与指标选取
本文数据来源于全国综合社会调查CGSS(2003),是中国人民大学于2003年和香港科技大学合作下,实施的中国第一次综合社会调查(GSS)。此次调查只包括城镇,共涉及了125个县级单位,559个居委会,5900名被访者,收回有效数据5894条。该调查的学术研究主题包括社会分层、社会流动和社会网络,具体指标包括:(1)住户成员部分(2)个人基本情况(3)户口变动(4)家庭情况(5)社会交往(6)教育经历(7)职业经历(8)目前职业等方面。本文根据需求选取了3317个样本,选取收入、教育水平、家庭总人口数、作为自变量,选取住房使用面积为因变量进行分析。
二、研究方法
本文采用SPSS18.0进行数据分析,在原始样本数据中,剔除那些回答不明或者作废的数据,采用线性回归分析方法研究现象。
三、变量
1、本文进行了三次分析,因变量分别为市值、使用面积和其他住房处,选取能够直观反映住房状况的住房使用面积作为因变量,按照惯例对因变量计算对数值,以便使其更接近正态分布。
2、收入水平,这一变量在cgss2003数据中用被访者“全年家庭总收入”这一数据表示。
3、受教育水平
4、家庭人口数,使用cgss2003中家庭人口变量,选取有效值重新编码为不同变量。
四、研究假设的确立
本文的主要目的是探讨样本的性别、教育程度、收入、家庭人口数对住房使用面积的影响,按照一般理解,性别的影响程度应该有一定区别;一般收入越高、住房面积也越大;一般而言,教育程度高,收入相应也会越高,推到住房面积也相应越大,但不可忽视社会中也存在相当部分低学历、高收入人群,暂时先预假设学历高,住房面积高;家庭人口数一般越多,住房面积越大,由此提出以下假设:
假设1:教育程度对住房面积存在影响,且教育程度越高,住房面积越大
假设2:收入对住房面积存在影响,且收入越高,住房面积越大
假设3:家庭人口数对住房面积存在影响,且家庭人数越多,住房面积越大
五、数据分析验证
(一)原始变量的统计描述与转换:
原始的变量中,教育程度为分类变量,先统计教育各个类别分布的人数与百分比,初步观测数据分布情况。
教育程度
教育程度统计结果可见,此次调查的样本中,初中人数最多,有989人,比例是29.8%,其次是高中学历,有624人,比例是18.8%,而最高学历硕士的人数是16人,比例是0.5%,为最少人群;再者,观察高等教育总人群,经过对比可以发现,此次调查的样本群,以低学历为主。
另外几个原始变量家庭人口数、收入、使用面积均为连续性变量,与分类变量不同,连续性变量的统计以均值、标准差为主要参考指标,以初步观察数据的分布特征。
描述统计量
家庭人口的统计结果可见,最小为1人的单身家庭,最多居然有16人的大家庭,总体均值为3.33人的正常数据,可见为常态。
描述统计量
收入统计结果可见,最小存在零收入者,最高的收入为300000,总体均值为11303.99,可见总体存在很大差距;同时,由于数据位数存在大的差距,通过SPSS运算的功能,除以10000,以消除数据差别。
描述统计量
最后是因变量使用面积的统计结果,可见:最小只有5平米,最高的有800平米,总体均值为61.606,可见总体差距很大。为了消除影响,将该变量去自然对数,以下是统计结果:
描述统计量
可见最小值为1.61,最大值为6.68,均值为3.93
(二)住房面积在不同性别、不同教育程度的差异检验:
性别与教育程度属于分类变量,首先验证一下住房面积是否存在显著差异,针对性别采用T检验,而教育程度由于是多分类,采用方差分析
1.住房面积在不同性别的T检验结果:
组统计量
以上即为不同性别的T检验结果,由显著性检验P值=0.80可知,不同性别的住房面积不存在显著差异,也就是说,性别的影响不显著。
2.住房面积在不同教育程度的方差分析结果:
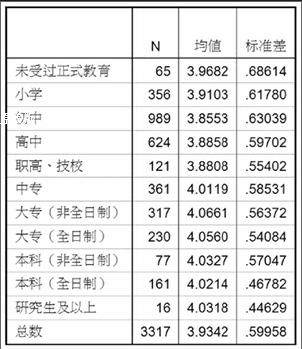
不同教育程度使用面积统计量
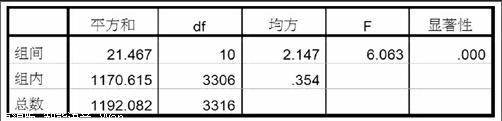
ANOVA
使用面积
以上为不同教育程度的住房面积的方差分析结果,由表格2的差异显著性检验结果可知,P值=0.000<0.05,表明不同的教育程度人群,住房面积存在显著差异,参考表格1的均值数据、以及均值图都可以发现:初中、高中、职高人群都处在相对较低水平,而2类大专、以及本科人群处在相对较高水平。其中,最高的是非全日制大专,均值为4.066,最低的是初中人群,为3.855。
1. 建立多元回归模型,研究性别、教育水平、收入、家庭人口数对住房面积的影响
模型汇总b
a. 预测变量: (常量), 家庭人口 , 性别, 教育程度, 年龄, 收入A。
b. 因变量: 使用面积
表格1首先给出的是自变量与因变量的复相关系数R、决定系数R方以及校正的决定系数调整R方,由结果可见,5个自变量与因变量的相关系数是0.266,此外,决定系数R方是检验回归方程拟合是否良好的指标,由决定系数R方值=0.071可知,5个自变量可以解释的因变量的变异是7.1%,相对较少;Durbin-Watson统计量是检验因变量的残差独立性的非常重要的指标,若该项指标不通过,则表明需要向模型中引入时间因素、或直接使用时间序列模型来分析,而不是普通的线性回归模型。
Durbin-Watson序列检验的判断标准是:若该值在2附近,则表明残差间是相互独立的,观测可知在此模型中该值=2.543非常接近2,表明无异常。
Anova b
a. 预测变量: (常量), 家庭人口 , 性别, 教育程度, 年龄, 收入A。
b. 因变量: 使用面积
表格2是模型的整体显著性检验结果,所用的是方差分析,可见F值=50.432,SIG值<0.05表明模型整体检验显著,若该值>0.05表明模型整体检验不显著,观测此处SIG值=0.000表明模型整体显著。
系数a
以上是整个回归方程结果中最重要的表格,是各自变量在回归方程中的检验结果,各个自变量的检验是否有意义主要是看SIG值,如果SIG值<0.05,表明该自变量在回归方程中是成立的,同时也说明该自变量对因变量的影响是显著的,如果SIG值>0.05,表明该自变量在回归方程中是不成立的,同时也说明该自变量对因变量的影响不是显著的。
性别的SIG值=0.366>0.05,表明对住房面积不存在显著影响,假设1得以认证;
教育程度的SIG值=0.000<0.05,表明对住房面积存在显著影响,考察回归系数值=0.025可知,教育程度为正向影响,也就是说教育程度高的住房面积相对也大,假设2得以验证;
收入的SIG值=0.000<0.05,表明对住房面积存在显著影响,考察回归系数值=0.037可知,收入为正向影响,也就是说收入高的住房面积相对也大,假设3得以验证;
家庭人数的SIG值=0.000<0.05,表明对住房面积存在显著影响,考察回归系数值=0.112可知,家庭人数为正向影响,也就是说家庭人数多的住房面积相对也大,假设4得以验证;
比较3个显著的自变量可以发现,家庭人数的影响程度最大、其次为收入水平,而教育程度的影响相对最低; 线性回归分析中多重共线性是可以通过指标来识别的,通常有方差膨胀因子、容差等等。此处我们以方差膨胀因子(VIF)为例,当0<VIF<10,不存在多重共线性;当10
见表格3最后的VIF统计量:3个自变量都是在1附近,容差统计量低于1,可见不存在共线性问题。
左两图分别为标准化残差的直方图以及PP图,由直方图可见,残差分布呈现出典型的正态分布特征,而PP图中可见散点围绕直线呈均匀上升,无异常点出现,可见回归方程的这一条件得到满足
六、总体结论
经过以上分析,验证了自变量教育程度、收入和家庭人口数对于因变量(住房面积)都有着显著的影响的同时,意外的是结果与研究假设有一定差异。回归方程总体验证物无共线性、残差独立性、分布正态性均得到满足,本身无重大缺陷。从研究结果回应研究假设来看,教育程度和收入以及家庭总人口数对住房面积的影响基本符合假设。
【参考文献】
[1]中国城市住宅问题研究会、住宅社会学学术委员会主编,《住宅社会学导论》 安徽出版社 1991年
[2]刘米娜. 中国城镇住房产权的区域差异分析——基于CGSS(2003)数据的实证研究[J]. 兰州学刊, 2009(5):114-119.
