强阻尼随机Kirchhoff方程的随机吸引子
2016-03-14秦闯亮杜金姬
秦闯亮,杜金姬
(信阳学院 数学与信息学院,河南 信阳 464000)
强阻尼随机Kirchhoff方程的随机吸引子
秦闯亮,杜金姬
(信阳学院 数学与信息学院,河南 信阳 464000)
讨论具有可加噪音的强阻尼随机Kirchhoff方程的随机动力系统,利用O-U过程对随机项进行处理,采用同构映射的方法,得到强阻尼随机Kirchhoff方程解的存在唯一性和随机吸引子的存在性.
O-U过程;随机Kirchhoff方程;随机吸引子
1 引言及预备知识
本文主要研究具有可加噪音的强阻尼随机Kirchhoff方程

其中:u=u(x,t)是D×[0,+∞)上的实值函数,D是Rn(n∈N)上具有光滑边界的有界开集;α>0;β>0;f(⋅),q(⋅)∈H01(D)IH2(D);g(⋅)∈C1(R,R);ρ>−1,且ρ为整数;qdW描述了一个可加白噪声;W(t)是概率空间(Ω,F,P)上的一维双边Wiener过程,Ω={ω∈C(R,R):ω(0)=0},F为Ω上由紧开拓扑生成的Borelσ-代数,P为概率测度[1].
设(Ω,F,P)是概率空间,{θt:Ω→Ω,t∈R}是一族保测度变换,映射(t,Ω)θtω是可测的,θ0=id ,且θt+s=θtθs(s,t∈R),则(Ω,F,P,(θt)t∈R)是一遍历度量动力系统,且θtω(⋅)=ω(⋅+t)−ω(t).
对于任意u,v∈L2(D),令内积,范数;对于任意,令内积,范数;对于任意u,,令内积范数.
2 解的存在唯一性及随机动力系统

由文献[2-4]可知,式(4)中的算子L是Hilbert空间E上的C0-半群eLt上的无限小生成算子,对每个ω∈Ω,函数E→E关于ϕ是整体Lipschitz连续的.由Hilbert空间E上的随机微分方程解的存在唯一性[5-6]可知,方程(4)对初值和每个ω∈Ω具有唯一解ϕ,即且
对任意t≥0,a.e.ω∈Ω.设从E→E的解映射,则定义了方程(4)在E上的一个随机动力系统.
因此,对随机动力系统S1(t,ω),只需考虑与其等价的随机动力系统S(t,ω).
3 随机吸引子的存在性
记空间E中的所有缓增子集合为D(E).
引理1[7]设,对任意,若,其中,有

引理2 设φ是问题(3)的一个解,则存在一个有界的随机紧集,使得对任意缓增随机集B(ω)∈D(E),都存在一个随机变量TB(ω)>0,使得



引理3 对任意B(ω)∈D(E),设φ(t)是方程(3)在初值φ0=(u0,u1+μu0)T∈B的解,它可分解为φ=φ1+φ2,其中:φ1,φ2分别满足

则



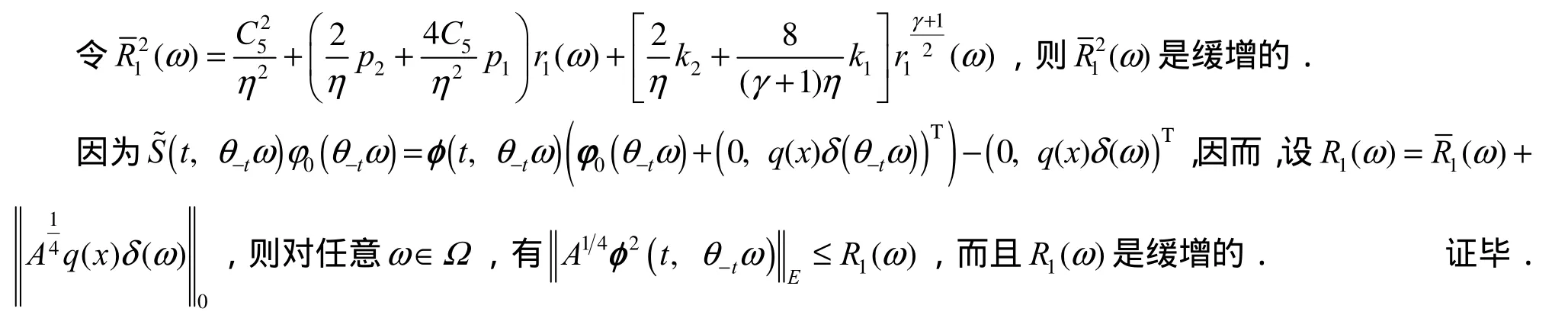

根据引理1~4,得到定理.
[1]ARNOLD L.Random dynamical systems[M].New York:Springger-Verlag,1998
[2]PAZY A.Semigroups of linear operators and applications to partial differential equations[M].New York:Springger-Verlag,1983
[3]Massatt P.Limiting behaviour for a strong damped nonlinear wave equation[J].J Diff Equ,1988(48):334-349
[4]FAN X.Random attractor for a damped sine-Gordon equation with white noise[J].Pacific J Math,2004(216):63-76
[5]CRAUEL H,NUALART D.Random nonlinear wave equations:Smoothness of the solutions[J].Probab Theory Related Fields,1988(79):469-508
[6]Prato G D,Zabczyk J.Stochastic equations in infinite dimensions[M].London:Cambridge University Press,1992:115-236
[7]Zhou S F.Global attractor for strongly damped nonlinear wane equations[J].Functional differential equations,1999,6(3-4):451-470
[8]Zhao Caidi,Zhou Shengfan.Sufficient conditions for the existence of global random attractors for stochatic lattice dunamical systems and applications[J].J Math Appl,2009(354):78-95
Random attractor for strongly damped stochastic Kirchhoff equation
QIN Chuang-liang,DU Jin-ji
(School of Mathematics and Information,Xinyang College,Xinyang 464000,China)
It is discussed that the stochastic dynamical system of the strongly damped stochastic Kirchhoff equation with additive white noise.By using O-U process to deal with random itemsanda dopting the method of isomorphic mapping,proves the existence and uniqueness of solution and the existence of random attractor for such an equation.
O-U process;stochastic Kirchhoff equation;random attractor
O211.63
A
10.3969/j.issn.1007-9831.2016.12.002
2016-09-20
信阳学院资助项目(2015yb42)
秦闯亮(1981-),男,河南许昌人,助教,硕士,从事随机动力系统研究.E-mail:qincl168@163.com
1007-9831(2016)12-0006-06
