具有庇护所效应的Kolmogorov型捕食-食饵系统的进一步研究
2016-03-14林琳冯晓梅
林琳,冯晓梅
(1.运城农业职业技术学院 基础教学部,山西 运城 044000;2.运城学院 应用数学系,山西 运城 044000)
具有庇护所效应的Kolmogorov型捕食-食饵系统的进一步研究
林琳1,冯晓梅2
(1.运城农业职业技术学院 基础教学部,山西 运城 044000;2.运城学院 应用数学系,山西 运城 044000)
研究了一类具有庇护所效应的Kolmogorov型捕食-食饵系统,运用Bendixson环域定理及丁荪红定理,得到了该系统存在唯一极限环的充分条件.运用Dulac函数法,得到了系统不存在极限环的充分条件.同时利用Matlab进行了仿真.
庇护所效应;捕食者;食饵;平衡点;稳定性;极限环
近年来,食饵具有庇护所效应的捕食系统已被许多人所研究,取得了比较好的成果[1-7],但对于Kolmogorov模型[8]的研究成果还不甚多见.文献[9]以Kolmogorov模型为基础,创建了一类具备庇护所效应的2种群食饵-捕食系统,本文在此系统基础上对其进行更深入的研讨.
1 数学模型的建立
文献[9]基于一系列的假设得到了模型

其中:x(t)为食饵种群在t时刻的种群密度;y(t)为捕食者种群在t时刻的种群密度;r为食饵种群固有的增长率;c为捕食者种群的死亡率;K为环境的容纳量;q为捕食者最大消耗率;p(c 当1−C−AC>0时,系统(2)共有3个非负平衡点:,其中: 文献[9]用常微分方程定性理论给出了系统(2)的平衡点类型及解的有界性.本文对此系统进行更深一步的研究. 定理1 设(A,C)∈,那么 为了更加明确地验证定理2的正确性,对系统(1)的一个具体例子进行数学模拟,用数形结合的方法验证其正确性. 令r=q=a=0.5,K=10,p=0.4,c=0.2,得到系统 图1γ=0.84<γ1=0.85时的数值模拟 图2γ1=0.85<γ=0.86<γ2=0.95时的数值模拟 图3γ2=0.95<γ=0.99时的数值模拟 [1]林琳,侯林洁.具有庇护所的Lotka-Volterra型的捕食-食饵系统[J].北华大学学报:自然科学版,2012,13(1):19-21 [2]周稻祥,朱长荣.一类具有常数避难所与收获率的捕食-食饵模型的稳定性[J].重庆理工大学学报:自然科学版,2012,26(12):122-126 [3]帅智圣,苗春梅,张伟鹏,等.具有庇护所的三种群捕食者-食饵模型[J].生物数学学报,2004,16(1):65-71 [4]徐昌进,陈大学.具有时滞的食饵-捕食模型的分支问题[J].重庆师范大学学报:自然科学版,2011(3):43-48 [5]徐国明,贾建文.一类具有避难所的捕食系统的分析[J].陕西师范大学学报,2007,21(4):4-7 [6]张艳波,王万雄,段永红.一类具第三类功能反应且食饵具有避难所的捕食系统的分析[J].数学的实践与认识,2010,40(24):149-154 [7]马智慧,李文龙,李自珍,等.具有已感染者庇护所效应的传染病模型[J].兰州大学学报,2008,44(2):111-114 [8]陈兰荪.数学生态学模型与研究方法[M].北京:科学出版社,1988 [9]林琳,雒志学.具有庇护所的Kolmogorov型的捕食-食饵系统[J].重庆理工大学学报:自然科学版,2014,28(2):120-122 [10]马知恩,周义仓.常微分方程定性与稳定性方法[M].北京:科学出版社,2001 [11]丁荪红.捕食者-食饵系统极限环的唯一性[J].科学通报,1985(13):976-979 The further study of the Kolmogorov predator-prey system with prey refuges LIN Lin1,FENG Xiao-mei2 Studies the Kolmogorov prey-predator system with prey refuges.The sufficient condition for the existence and the unique of the limit cycle is given by using the Bendixson and Ding Sunhong theory.The sufficient condition that the system has no limit cycle is obtained by the Dulac function.The theory is illustrated by using the Matlab. prey refuge;predator;prey;equilibrium point;stability;limit cycle O175.1:Q141 A 10.3969/j.issn.1007-9831.2016.12.001 2016-10-13 国家自然科学基金资助项目(11501498) 林琳(1983-),女,山西运城人,讲师,硕士,从事生物数学研究.E-mail:15835988676@163.com 1007-9831(2016)12-0001-05
2 主要结果及证明


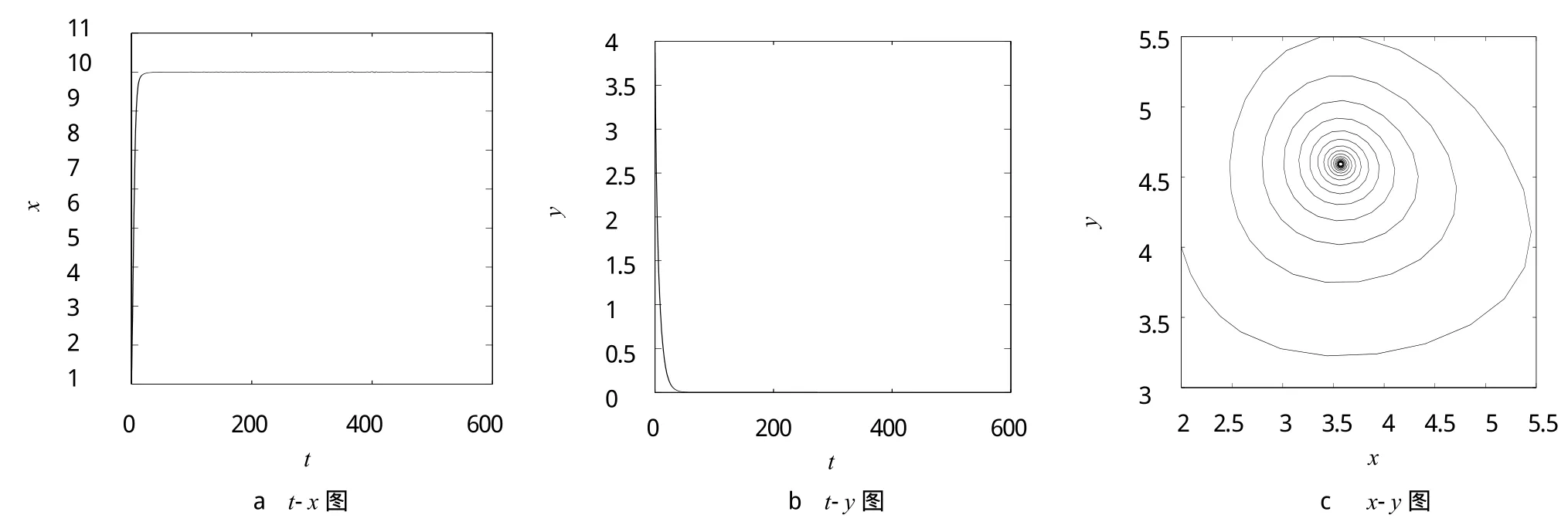
3 实例仿真



(1.Department of Primary Education,Yuncheng Polytechnic College of Agriculture,Yuncheng 044000,China;2.Department of Applied Mathematics,Yuncheng University,Yuncheng 044000,China)
