城市空气污染数据的分析与研究
2016-03-14杨小雷汤凤香
杨小雷,汤凤香
(佳木斯大学 理学院,黑龙江 佳木斯 154007)
城市空气污染数据的分析与研究
杨小雷,汤凤香
(佳木斯大学 理学院,黑龙江 佳木斯 154007)
针对日益严重的大气污染问题,基于现有数据与相关研究,采用相关分析法,对AQI指标之间的相关性进行了定量分析.利用主成分分析,确定PM10为被解释变量,其它4种污染物为解释变量,应用逐步回归分析方法及多元回归分析,通过逐层分析比较得到了PM10与PM2.5,CO,SO2,NO2的最优二次回归模型.
空气污染;相关分析;主成分分析;逐步回归分析
1 问题背景
1.1 问题的提出
近年来,随着城市空气污染的加剧以及广大民众对生活环境与质量要求的日益提高,空气质量(AQI)越来越受到广大民众与政府相关部门的重视.AQI主要指标有PM10,PM2.5,CO,NO2,SO2,探究这些污染物之间关系对空气污染的治理具有一定的现实意义.
1.2 模型假设
假设1 监测数据是用统一的设备配置与标准获得的;
假设2 所有空气质量数据的误差均相互独立,并且服从正态分布
假设3 空气质量的5个指标,其监测是相互独立的.
1.3 符号说明
本文中2σ为方差;α为显著性水平,一般设为0.05或更小,本文设为0.01;y表示PM10的值;x1表示PM2.5的值;x2表示CO的值;x3表示NO2的值;x4表示SO2的值.
2 模型求解
2.1 预备知识
2.1.1 相关分析 在直线相关条件下,相关系数是2个变量x和y之间相关关系的方向和密切程度的综合性指标[1],记为r,则有
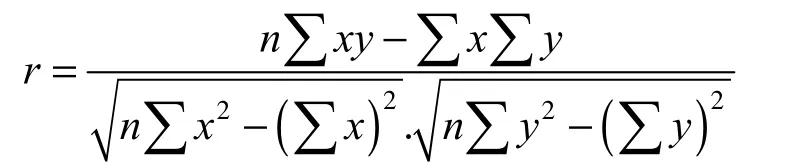
其中:n为样本容量;r取正值或负值决定于分子协方差;r的绝对值在0与1之间,其绝对值大小可说明现象之间相关关系的紧密程度,具体标准为:当时,变量x和y没有关系;当时,变量x和y低程度相关;当时,变量x和y呈显著相关;当时,变量x和y呈高度相关.
2.1.2 主成分分析 主成分分析也称主分量分析[2-3],旨在利用降维的思想(本文利用其性质即贡献率)把多指标转化为少数几个综合指标.
具体分析步骤为:
Step3 对m个主成分进行综合评价.对m个主成分进行加权求和,即得最终评价值,权数为每个主成分的方差贡献率.
Step4 求KMO测度.
该方法是SPSS提供的判断原始变量是否适合作主成分分析的统计检验方法之一,它比较了观测到的原始变量间的相关系数和偏相关系数的大小.一般而言,KMO测度大于0.5意味着因子分析可以进行,当KMO的测度大于0.7时,则其是令人满意的值.
对于n组独立观测值,设,其中:相互独立.设最小二乘法就是选择β0和β1的估计和,使得,而此时yi所对应的值称为回归值,记为.
回归直线与各观测点的接近程度称为回归直线对数据的拟合优度.为了说明直线的拟合优度,引进判定系数
(2)当R2=1时,原始数据的总变异完全可以由拟合值的变异来解释,并且残差为零,即拟合点与原始数据完全吻合;
(3)当R2=0时,回归方程完全不能解释原始数据的总变异.
判定系数,一方面反映了解释的变异占总变异的百分比,从而说明回归直线拟合的优良程度;另一方面,它从相关性的角度,说明原因变量y与拟合变量的相关程度,从这个角度看,拟合变量与原变量y的相关度越大,拟合直线的优良度就越高.
2.1.4 多元回归分析 多元回归分析可以看成是一元线性回归分析的扩展[5].多重判定系数2R是多元回归中回归平方和占总平方和的比例,它是度量多元回归方程拟合程度的一个统计量,反映在因变量y的变差中被估计的回归方程所解释的比例.
对于多重判定系数有一点需要注意:给模型增加自变量时,多重判定系数也随之增大,然而多重判定系数的代价是残差自由度的减少,因为残差自由度等于样本个数与自变量个数之差.自由度小意味着估计和预测的可靠性低.这表明,当一个回归方程涉及的自变量很多时,回归模型的拟合从表面上看是良好的,而区间预测和区间估计的幅度却变大,以致失去实际意义.为此,利用样本量n和自变量的个数k去调整,计算出调整的多重判定系数,记为,其计算公式为
2.2 数据的预处理与被解释变量的确定
2.2.1 数据的处理与相关分析模型的求解 本文采用广东省东莞、深圳和广州3个地区从2014-06-01—2015-05-31的空气质量监测数据.由于收集的数据有缺漏,存在一些缺省值,所以在分析时首先利用SPSS对其缺省值进行了直接剔除,得到可用于统计分析的数据集(见表1)(由于篇幅限制,仅示意性列出最前2次与最后1次观测值).3个城市的空气质量数据经预处理后,由SPSS Pearson[6-8]求得AQI的5种指标之间的相关矩阵表(见表2).

表1 广东省东莞、深圳和广州3个地区空气污染数据

表2 5种空气质量指标间的相关矩阵
由表2可以看出,联系最为紧密的监测指标组依次为:(PM2.5,PM10),(PM10,NO2),(PM10,CO),(PM2.5,NO2),且PM10与PM2.5间相关系数为0.929,呈高度正相关,且相关系数相对较大;PM10与CO,NO2,SO2间相关系数分别为0.683,0.706,0.572,呈显著正相关,且除了SO2与CO之间的相关系数低于0.572以外,其余各指标之间相关系数均超过0.572,且均在α=0.01水平上显著,因此各指标之间显著相关.
2.2.2 运用主成分分析求解AQI的被解释变量 利用主成分分析法对AQI中5项监测指标求解KMO,进行Bartlett的检验,并求取解释的总方差(见表3~4).

表3 KMO和Bartlett的检验

表4 解释的总方差
由表3可以看出,KMO测度为0.805>0.7,表示变量之间的相关性很好;而Bartlett球形度检验中的显著性水平值为0,达到了极其显著水平,这表明原变量之间具有明显的结构性和相关性,可以进行主成分分析.
由表4可以看出,PM10的特征值为3.476,方差贡献率为69.523%,是方差贡献率最大的一个主成分.因此,可以确定PM10为被解释变量,PM2.5,NO2,CO,SO2为解释变量.
2.3 求解PM10最优回归模型
2.3.1 PM10与PM2.5,CO,NO2,SO2多元一次及二次线性回归模型求解 由于PM10与PM2.5,CO,NO2,SO2等指标之间具有一定的相关性和独立性,应用Matlab的regress(Y,X,α)函数[9],对多个候选回归模型进行逐步回归,分别求得多元一次回归方程
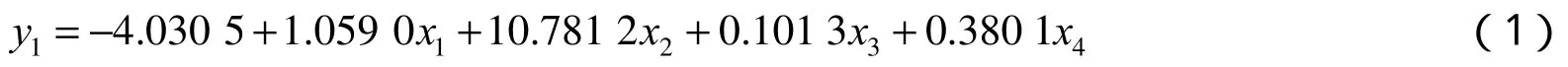
与多元二次方程

2.3.2 PM10与PM2.5,CO,NO2,SO2多元二阶多项式回归模型求解 考虑到两两因素之间的交互关系,应用Matlab对PM10的多元二阶多项式回归模型进行求解,得
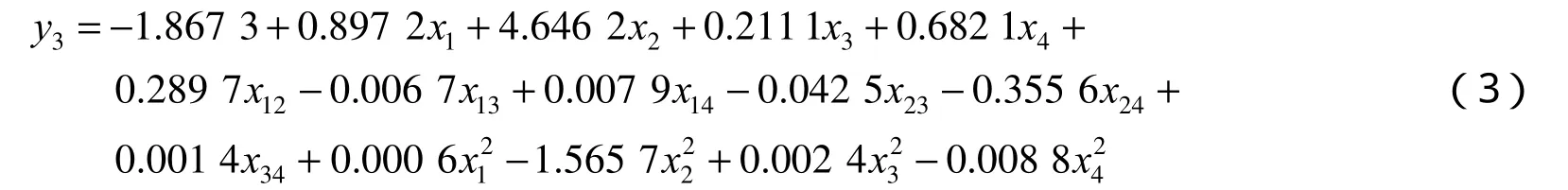
3 模型评价
3.1 模型的优点
(1)通过逐层比较,建立了相对优化的多元二阶多项式回归模型,得出了令人满意的结果;
(2)通过所求多元二阶多项式回归模型的置信区间可以用来判断一些数据的真实性;
(3)利用多元二阶多项式回归模型可以通过控制变量来预测某一数据或数据走势;
(4)可以做出关于PM10的多元二阶非线性回归模型(3)的残差分析图,直观感受模型的拟合程度;
(5)所有样本信息结合在一起分析,增加了分析的可靠性.
3.2 模型的缺点
(1)通过网络搜集到的数据本身可能存在不真实性,从而导致建立的模型不能准确地辨别出不真实的数据;
(2)由于地域差异性的存在,使得建立的模型不能适应所有地区的空气质量数据;
(3)PM10与PM2.5,CO,NO2,SO2的多元高阶回归模型可能效果更佳,因此还可以继续探究PM10与PM2.5,CO,NO2,SO2的多元高阶关系.
[1]贾俊平,何晓群,金勇进.统计学[M].北京:中国人民大学出版社,2012:30-31
[2]张志涌.MATLAB教程[M].北京:北京航空航天大学出版社,2010:20-25
[3]杜强,贾丽艳.SPSS统计分析从入门到精通[M].北京:人民邮电出版社,2011:18-20
[4]何晓群,刘文卿.应用回归分析[M].北京:中国人民大学出版社,2015:48-55
[5]何晓群.多元统计分析[M].北京:中国人民大学出版社,2004:21-23
[6]谢志英,刘浩,唐新明.北京市近12年空气污染变化特征及其与气象要素的相关性分析[J].环境工程学报,2015,9(9):4471-4478
[7]邓霞君,廖良清,胡桂萍.近10年中国主要城市空气API及与气象因子相关性分析[J].环境科学与技术,2013,36(9):70-75
[8]杨光霞,谢华.SPSS数据统计与分析[M].北京:清华大学出版社,2014:54-60
[9]司守奎,孙玺菁.数学建模算法与应用[M].北京:国防工业出版社,2012:45-50
Analysis and study of urban air pollution data
YANG Xiao-lei,TANG Feng-xiang
(School of Science,Jiamusi University,Jiamusi 154007,China)
Aiming at increasingly serious air pollution problems,use correlation analysis to make an quantitative analysis for the correlation between the AQI indicators based on existing data and the related research, and principal component analysis is used to determine that PM10is the explained variable,the other four kinds of pollutants are explained variable.Using stepwise regression analysis method and multiple regression analysis,through analysis step by step and comparison get the optimal quadratic regression model between PM10and PM2.5,CO,SO2,NO2.
air pollution;correlation analysis;principal component analysis;stepwise regression analysis
O213.1
A
10.3969/j.issn.1007-9831.2016.12.003
2016-07-30
佳木斯大学科研项目(13Z1201585)
杨小雷(1991-),男,安徽宿州人,在读本科生.E-mail:577560628@qq.com
汤凤香(1978-),女,黑龙江安达人,讲师,硕士,从事应用数理统计研究.E-mail:54993661@qq.com
1007-9831(2016)12-0012-05
