一种用于描述引力波中测地线的Henon-Heiles修改模型的模拟方法※

南 楠周天宏

(1.湖北汽车工业学院，湖北 十堰 442002；

2.武汉商学院，湖北 武汉 430056)

一种用于描述引力波中测地线的Henon-Heiles修改模型的模拟方法※

南 楠1周天宏2

(1.湖北汽车工业学院，湖北 十堰 442002；

2.武汉商学院，湖北 武汉 430056)

用MATLAB探索了一种模拟Vesely和Podolsky提出的适用于自由粒子在真空引力性PP波中的运动情况的Henon-Heiles修改模型动力学特性的方法。直接分析其势函数并通过庞加莱截面法探究该修改模型的动力学性质以及计算最大李雅普诺夫指数分析系统的稳定性情况，直观的反映了该模型的混沌现象。

MATLAB;Henon-Heiles模型；庞加莱截面;李雅普诺夫指数；混沌

一、引言

（一）原始Henon-Heiles模型和修改模型

经典的Henon-Heiles模型将研究物体的运动简化在由x，px，y，py表征的四维空间内，规范化后的Henon-Heiles哈密顿表达式（无量纲）可表示为[1]

直角坐标系：

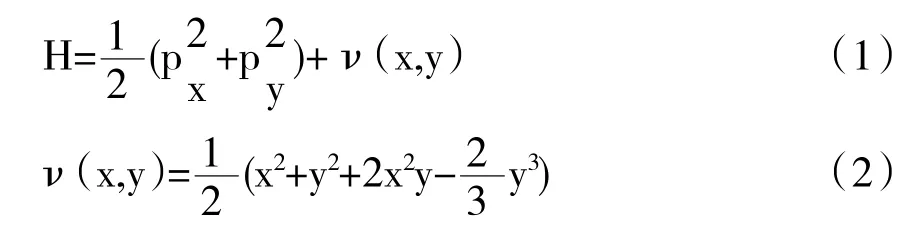
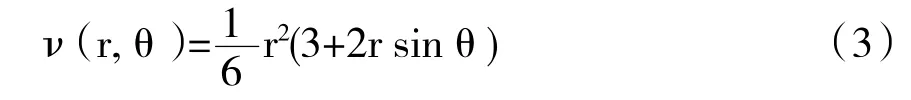
为模拟自由粒子在真空引力性PP波中的运动情况，Vesely和Podolsky提出了一种势能函数的修改模型[2]

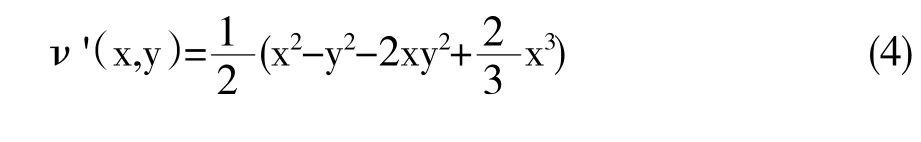
极坐标系：

为便于软件模拟，这里尝试稍作处理，运用变量代换，使之更接近原始模型的形式：

后可以写作新的形式：

根据正则方程有：

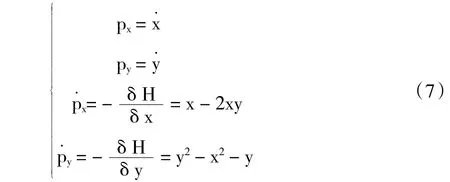
在平衡点处有：

从而根据（6）（7）确定平衡点的范围是

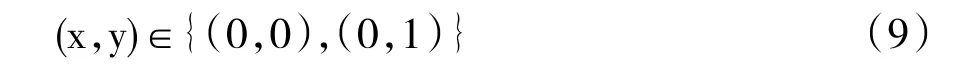
该模型势能函数的立体曲面图如图1所示。

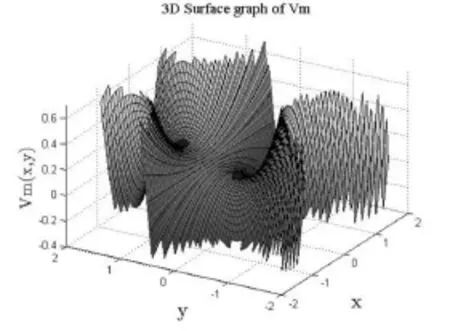
图1 修改模型势能函数Vm的三维曲面图（两个平衡点已在图中标出）

在图1中用蓝色标出的两个点是上述的平衡点（0,0）和（0,1），这两个点均是势能曲面的鞍点，且有V（0，0）=0，V（x，1/2）=1/12，V（0，1）=1/6.同时画出该势能函数模型在x-y平面的强度图，如图2所示。

图2 势能函数在x-y平面的强度图（包含一些等势线）

在图2中，黑色和紫红色实线分别代表V=1/12和V=1/6的等势线，在红色点（0,0）处，V=0。这样就将体系的运动情况限定在（0,1/12）和（1/12,1/6）两个能量区间来讨论[2,3]。

（二）最大李雅普诺夫指数

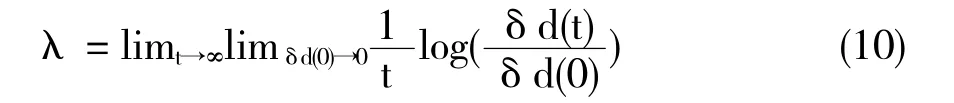
最大李雅普诺夫指数定义为δd是t时刻相空间轨迹上的一点与相邻轨迹上研究对象点的距离，λ表征的是相空间中初始时刻相近两点在运动过程中的平均指数偏离率[4]。λ为正值说明相邻轨迹点呈偏离趋势，最终进入混沌状态，为负值说明系统将趋于稳定[5]。

二、研究方法

在允许的能量范围（0,1/6）内选取六个能量值（E=1/25,E=1/12,E=1/10,E=1/8，E=1/7，E=1/6），并在相空间中各能量值允许的边界范围内均匀地选取数个初始条件点（这几个点在相同的能量面上），用四阶龙格库塔方法画出(y,Py)空间的庞加莱截面来研究其动力学性质，计算最大李雅普诺夫指数λ分析系统的稳定性和混沌性。在计算λ时，为了数值计算方便取小的时间间隔T（T=0.15s），并以相空间轨迹上N（N必须足够大，结果才会稳定收敛[5,6]，故取N=1000）个间隔为T的时间点为研究对象，计算λ的平均值作为其数值解。其形式为：

取N=1000，初始条件点分别选在庞加莱界面的轨道规则区域(样点为(y=0,Py=0))和混沌区域(样点为(y=0,Py=0.2))。程序会自动选取初始时刻跟它们相距很近的另一个初始点，求得一定能量下λ随积分时间的关系。

三、结果与讨论

通过对运动方程 (7)的积分，所得的Henon-Heiles修改模型的庞加莱截面如图3(a)(b)(c) (d)(e)(f)所示。

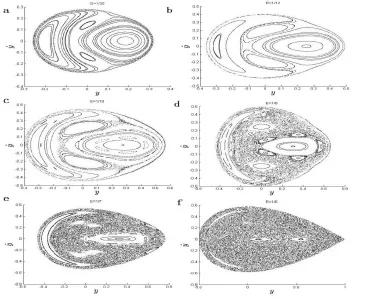
图3 不同能量E下系统的庞加莱截面图样

当0＜E＜1/12时，系统处于比较稳定状态，相空间由一系列准周期轨迹组成，且关于y˙=0成轴对称,如图3（a）和图3（b）所示。随着能量的增加轨道形状开始变形，规则性被打破，离散的点开始增多，但是稳定轨道依然存在，如图3（c）（d）（e）直到E增加至最大能量1/6，出现了大片密集的混沌点，只剩两个分离的“岛形”区域,如图3（f）所示。故当能量低于1/12时，体系始终稳定，混沌起始点出现在1/12＜E＜1/6区间内。在混沌区和规则区所选初始条件点的最大李雅普诺夫指数λ随积分时间的变化关系，结果如图4(a)(b)(c)所示。

图4 混沌区的初始条件点(y=0,Py=0.2)和规则区的初始条件点(y=0,Py=0)的最大李雅普诺夫指数λ在能量E=1/6下随积分时间的函数关系

正如图4（a）和（b）所示，λ随时间而无规则振荡，但总的趋势是随时间趋于稳定，最后收敛于一个特定值。如图4(a),λ始终在正方向振荡，最后收敛于一个正值（为0.0115），说明不规则区域的点是不稳定的，最终进入混沌状态。而规则区域的点很快便振荡于负方向，最后收敛于一个负值（为-0.0017），如图4（b）所示，说明稳定区域的点始终保持稳定的准周期运动状态。两个初始条件点在相空间图的对应位置如图4(c)所示。

四、结论

运用MATLAB软件对Henon-Heiles修改模型的庞加莱截面图样进行分析，结果证明当能量较低时，系统处于稳定状态，轨迹是一系列规则轨道。随着能量的增加，体系的不稳定性增强，规则性减弱，能量在（1/12,1/6）区间时，混沌现象开始明显，直至增加到最大能量（E=1/6）时，观察到了像原始模型中那样明显的大片密集混沌点。以稳定区一点和不规则区一点为初始条件点，计算了能量E=1/6时最大李雅普诺夫指数λ随时间的变化关系。当研究点在稳定区时，收敛于负值，体系始终趋于稳定。而对于不规则区域则逐渐收敛于正值，体系的无规则运动增强。到达限定能量值时，在很短时间内振荡至正方向，并收敛于一个正值。体系的相空间图和李雅普诺夫指数随时间的演化趋势均反映了该系统的混沌特性。

[1]Henon M and HeilesC.Astron,1964(69),73-79.

[2]K.Veseley,J.Podolsky.Physics Letters A,2000(271).

[3]王培杰，吴国桢.周期轨迹与不可积体系的量子化：Henon-Heiles体系的一个研究例子[J].物理学报,2005(6):2545-2551.

[4]HerbertGoldstein，Charles P.Poole，John L.Safko 2001 ClassicalMechanics(Third Edition,English)(Addison-Wesley).

[5]罗利军,李银山,李彤等.李雅普诺夫指数谱的研究与仿真[J].计算机仿真，2005（22）.

[6]刘昌伟.关于李雅普诺夫指数的Jacobi算法[J].武汉工程大学学报,1997(4).

责任编校：饶 敏

Simulation of AM odified Henon-HeilesM odelDescribing Geodesics in GravitationalW aves

NAN Nan1ZHOU Tian-hong2
(1.HubeiUniversity of Automotive Technology,Shiyan,Hubei,442002,China;
2.W uhan Business University,W uhan,Hubei,430056,China)

The paper,with the help ofsoftwareMATLAB,explored amethod to simulate the dynamic property of modified Henon-Heilesmodelapplicable in describing themotion of testparticle in PPwave proposed by Vesely and Podoisky.It directly analyzed the potential function and dynamic property of themodified model through Poincare surface of section;then it calculated the biggest Lyapunov exponent to check the stability of the system,which evidently showed the chaosof themodel.

MATLAB;Henon-Heilesmodel;Poincare surface ofsection;Lyapunov exponent;chaos

O412.1

A

2095-7955（2016）06-0079-03

武汉市教育局教研项目（项目编号：2013030）。

2016-11-19

南 楠（1988—），湖北汽车工业学院理学院教师，硕士。主要研究方向：材料学理论及测试技术；

周天宏（1963—），本文通讯作者，武汉商学院信息工程学院教授，硕士。主要研究方向：计算机科学及数学。