沪深300股指期货套期保值比率实证研究
——风险最小化下
2016-03-13余旭瑄
余旭瑄
(安徽财经大学金融学院,安徽 蚌埠233000)
1 引言
股指期货是金融期货的一种,是一种标准化期货合约。相比一些欧美发达国家,股指期货在中国产生较晚,它的发展经历了一个漫长坎坷的过程,但因为股指期货在产品定价、风险管理等方面的广泛应用,中国金融市场从未停止过对它的理论研究和实践探索。上海交易所和深圳交易所分别成立之后,中国金融市场和交易制度也日趋完善,越来越多的投资者选择进入股票市场进行投资。中金所(中国金融期货交易所)于2010年4月正式推出沪深300股指期货,标志着中国股指期货交易进入了一个新的发展阶段。之后,股指期货成为广大投资者进行资产管理中不可或缺的一种金融工具。与商品期货不同的是,股指期货的标的物是股票指数。在现实的投资当中,通过买卖股票,然后卖出一定的股指期货,达到股指期货套期保值的目的,不仅减少了现货价格波动,也规避了一定的系统风险,使投资者避免收到由于系统风险而带来的损失。股票市场存在系统风险和非系统风险。系统性风险由市场决定,受到整个宏观经济的影响。而非系统风险指的是单个股票价格发生波动的可能性,根据资产组合理论,非系统风险可以通过资产组合的方式达到有效降低。加之在通过在期货市场进行套期保值,投资者可以很好的规避系统风险。在实际操作中,为了获取最大的收益,降低投资风险,在股票品种和权重选择时就要尽量使其达到最优套保比率。
2 文献综述
Ohnson&Stein经过研究提出了使期货与现货组合收益方差最小化的套期保值方法。即投资者将期货资产和现货资产进行投资组合,为实现风险最小化,再根据这一组合的预期收益及风险(方差),确定其在现货市场及期货市场交易头寸的分布。在Ohnson&Stein基础上,Johnson给出了商品期货基于最小二乘法的最优套期保值比率的计算公式。Ederington在Johnson的基础上进一步指出:“用最小二乘法对现货价格及期货价格进行回归所得的可决系数的数值可以判断套期保值的效果如何。”
Engle和Granger两位学者进一步提出:“现货价格和期货价格两个时间序列之间存在某种协整关系,即使短期出现均衡误差,还是可能出现长期的均衡。”所以基于最小二乘法的套期保值策略并不准确。在这种前提下,这两个时间序列之间必然存在一个误差修正表达式,也就是误差修正模型(ECM模型)。
对于股指期货的套期保值,国内很多学者也做了一定程度上的研究。
胡向科在其所著的《不同估计模型最优套期保值比率绩效研究》中介绍了几种套期保值比率的估算方法。分别建立OLS、ECM-GARCH等模型对最优套期保值比率进行了估计。得出在方差最小化的原则下用ECM模型估算出的套期保值比率最好。
吴博在其所著的 《股指期货套期保值模型选择和绩效评价——基于沪深300股指期货仿真交易数据的实证分析》中在沪深300股指期货仿真交易数据的基础上,选取现货组合,通过“风险最小化”和“效用最大化”两大原则运用OLS、VAR、ECM、GARCH等不同模型进行套保的实证分析和效果比较,最后发现OLS模型可以使投资者取得效用最大化;GARCH模型则可以最大程度降低风险;而对样本外数据来说,误差修正模型套期保值不论在风险还是绩效控制上都是最优的。
综上所述,可知最小二乘回归模型是最基础的模型,而ECM模型是相比较而言套期保值效果较好的模型,本文选取OLS最小二乘模型、ECM模型来估算最优套机保值比率。
3 最优套期保值比率的实证模型
3.1 OLS(回归)模型
OLS模型原理是构建股指期货和股指现货价格的线性回归,采用最小二乘法估计出模型,方程中的斜率就是最优套期保值比,模型为:
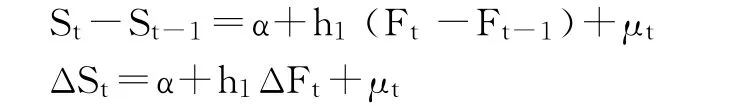
其中h1是方程的斜率,也就是所求的最小风险套期保值比率(St—t时刻的现货价格,Ft—t时刻的期货价格,St-1—t-1时刻的现货价格、Ft-1—t-1时刻的期货价格,α-截距项,μ1—随机误差项)。
1987年,Witt在对期货收益率和现货收益率取对数的基础上进一步提出了另一种最小二乘法模型的回归方程:
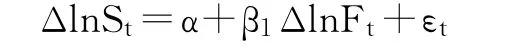
ΔlnFt和ΔlnSt分别表示t时刻期货和现货收益率的对数形式,斜率β1即为最优套期保值比率(α为截距项,εt为随机误差项)。公式如下:
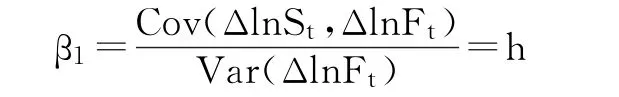
很多学者发现仅仅依靠大量历史数据的简单线性回归得到的最优套期保值比率是不够准确的,残差项序列相关会对OLS方法的运用造成一定的影响。并且,因为运用最小二乘法的前提严格要求残差序列相互独立且不相关,OLS模型忽略了这点。所以用最小二乘法得到的“最优”套期保值比率并不是最优的。
3.2 ECM 模型
金融时间序列通常呈现非平稳性,但它们的一阶差分却都是平稳的,而OLS模型忽略了这一点。直到Granger和Engle两位学者研究提出了序列间存在协整关系的误差修正模型:
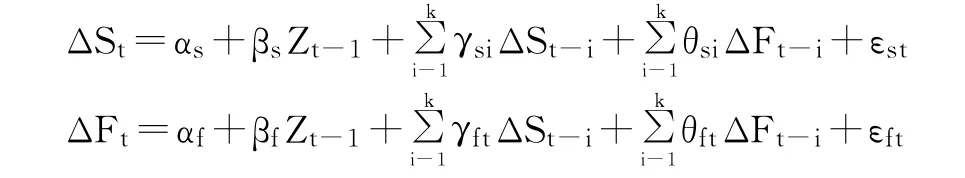
系数βs和βf表示两个市场对于长期均衡关系的偏离反映的速度。如果现货价格St和期货价格Ft之间的协整向量表示为(1,-β),则误差修正项Zt-1=St-βFt(ΔSt—t时刻现货价格收益率,ΔFt—t时刻期货价格收益率,ΔSt-i—t-i时刻现货价格收益率,ΔFt-i—t-i期货价格的收益率,εst、εft—服从独立同分布的随机误差项)。
Ghosh提出了考虑两序列协整关系的最小风险套期保值比率的ECM模型:

ECM模型相比OLS模型在方程中增加了一个误差修正项,Ghosh指出:“误差修正项考虑了期货价格和现货价格的非平稳性、短期动态关系和长期均衡关系。”就是所要估计的最小风险套期保值比率(α-截距项,m-现货收益率最佳滞后值,n-期货价格收益率最佳滞后值)。
4 数据选取、处理及检验
4.1 数据的选取
4.1.1 趋势图分析
本文选取了2014年5月9日至2015年12月23日区间内沪深300股指期货和沪深300指数的日收盘价。由于不同到期日的期货合约的收盘价不同,因此选取每天成交量大的期货合约的收盘价作为股指期货的收盘价。将股指期货合约的收盘价与沪深300指数的收盘价画出折线图,见图1。
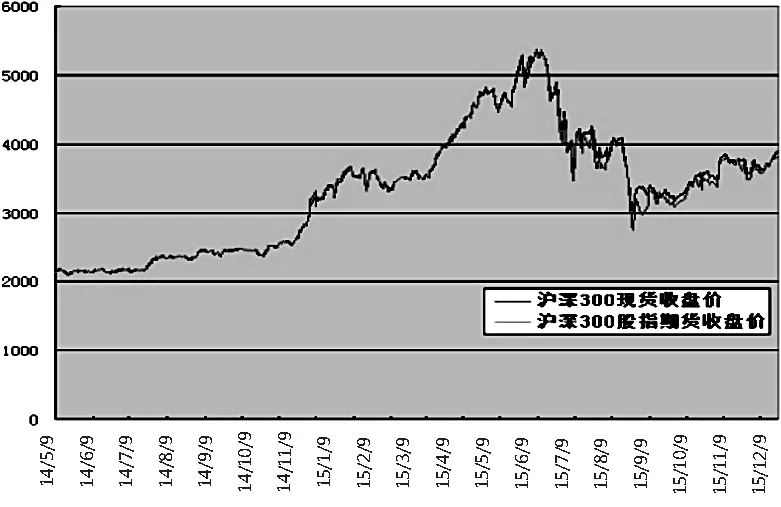
图1 收盘价曲线
由图可知,沪深300指数收盘价与沪深300股指期货收盘价走势相同,因此,可以利用两者进行套期保值,且两者之间相关系数很高。
4.1.2 基差分析
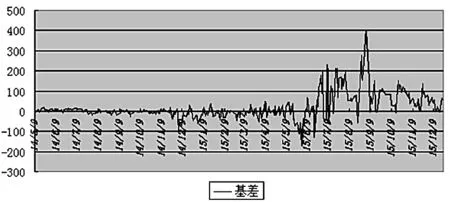
图2 收盘价基差曲线
由两者基差图可知,基本走势偏离不大,基差风险趋于平稳。
4.2 数据平稳性的检验
将每日现货和期货收盘价格取自然对数,分别用lnFt、lnSt表示,然后其进行平稳性检验。采用的方法是单位根检验。
用Eviews软件对股票期货收益率和股票现货收益率进行ADF检验,并对原序列做单位根检验,可知两者统计量ADF比三种显著性水平下的临界值都小,即序列的一阶差分是平稳的,DLNS序列和DLNF都为一阶单整序列。
4.3 数据协整关系的检验
由前面的平稳性结果可知,序列满足检验协整关系的前提。建立以下关系式:
S=1.002F+14.8355
对其残差项ε进行ADF分析,结果如图3。

图3 残差项εADF分析图
由图可知在1%显著性水平下序列S、F存在协整关系,满足建立误差修正模型的前提。上述关系式即为两个序列的协整方程,可以进行后续的模型研究。
4.4 最优套期保值比率的研究
4.4.1 OLS模型
将现货对数收益率作为因变量,期货对数收益率作为自变量,构建两者的线性回归方程,用Eviews软件做回归,估计得出最优套期保值比率。得到回归方程如下:
dlnSt=0.000456+0.715779dlnFt+εt
估计得出斜率β=0.715779(εt-随机干扰项)。可见,OLS模型下的最优套期保值比率为0.715779。从判定系数R2、F统计量和DW值来看,方程对数据拟合度是比较高的。
4.4.2 建立误差修正模型
用Eviews软件建立沪深300现货、期货对数收益率及其残差三者之间的关系,得到方程如下:
dln S=0.000336+0.705096ln F-0.095039·d lnS(-1)+0.177121d lnF(-1)+Z
方程中的Z(ECM)即前面协整方程得到的。可知最优套期保值比率为0.705096,拟合优度R2=1。
4.4.3 套期保值最优比率和绩效比较
在得到OLS模型和ECM模型估计的套保比率之后,为了便于套期保值效果的分析,可以对两种模型的套期保值绩效进行比较。由套期保值绩效计算公式:
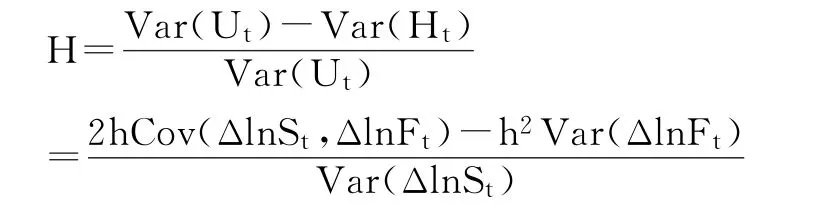
并综合上文可得表1。

表1 套期保值最优比率和绩效比较
从表可知,在两种套期保值模型估计的套期保值比率中,OLS模型估计的值较误差ECM模型估计的值略高,但两者都较高,表明股指期货与股指现货的价格走势基本一致,即投资者进行套保时面临的基差风险比较小。由表中数据还可以看出,两种模型的套期保值绩效的指标值都较高,均在0.91之上。这表明套期保值取得很好的效果,可以让投资者规避市场中极大一部分的风险(90%)。表中接近于1绩效表明,对沪深300现货指数而言,各模型的套期保值是有效的。而基于收益风险最小化套期保值理论下,ECM模型的套期保值效果最好。
5 结论
最优套期保值比率的估计以及套期保值的效果是本文的研究重点。由本文可知:在这两种模型估计的套保比率中,各种模型彼此之间没有太大的差异,股指现货与股指期货的价格走势基本一致,投资者投资面临的基差风险比较小,整个市场的系统性风险并不算太高。由计算出的套期保值比率小于1,说明两种头寸构成的投资组合中期货头寸数量较少,投资者为此付出的成本较低。通过本文的研究,各模型的套期保值绩效相较而言,ECM模型的套期保值效果最好,根据其计算出的套保比率来选择投资组合可以有效的规避系统风险。本文仅选取了两种常用的模型对套期保值进行研究,而对于一些更加复杂的模型比如GARCH模型、BEKK模型等未做介绍,哪一种模型在套期保值中更为有效这个问题还有待更进一步的研究。
[1]Johnson L.The theory of hedging and speculation in commodity futures[J].Review of Economic Studies,1960,27(3):139-151.
[2]Ederington LH.The hedging performance of new futures markets[J].Journal of Finance,1979,(34):157-170.
[3]A.Ghosh.Hedging with Stock Index Futures:Estimation and Forecasting with Error Correction Model[J].Journal of Futures Markets,1993,(13):743-752.
[4]吴博.股指期货套期保值模型选择和绩效评价——基于沪深300股指期货仿真交易数据的实证分析[J].新金融,2010,(02):29-33.
[5]胡向科.不同估计模型最优套期保值比率绩效研究[J].经济视角(下),2010,(01):73-75.
