基于线性规划的直送与配送区域划分

苏亚州 高 阳

(合肥工业大学商学系,安徽 合肥230000)

1 引言

物流活动作为生产运作的重要环节之一,它的活动方式根据流动中的物品的位置是否发生移动可以分成线路活动和节点活动。运输活动作为物流功能要素之一,因货物必须通过运输工具的承载才能在运输线路上移动并送达异地,故而运输活动也是线路活动的一种。

直送与配送虽然都属于线路活动,但是两者之间有着迥乎不同的区别。主要体现为以下几点:

(1)运输线路组成中节点的个数不同。直送式运输,一般是指由一个供应点对一个客户的专门送货,一般是一个工厂只向一家客户送货。配送式运输,一般是指由供应点先将货物送往配送中心,再将货物从配送中心送往客户手中。

(2)运输线路运载能力利用率不同。采用直送运输方式送货时,往往会因客户需求的变化,而使得供应商的运输车辆难以满载运输,进而影响整个线路运载能力利用率。采用配送运输方式,将货物由供应点先送往配送中心的过程中,可以利用配送中心的储存功能将客户的需求变动对线路运载能力利用率的影响降到最低,进而充分利用整个线路的运载能力。

(3)运输线路复杂程度不同。直送式运输,由一个供应点对一个客户的专门送货,线路简单。配送式运输由于运输过程中要经过配送中心,并且可能存在同时向多个客户送货的可能,因而线路较为复杂。

2 直送与配送区域划分模型构建

2.1 直线上运输成本临界点的确定

商品运输过程中,商品直送过程中可能会出现中转到配送中心暂存再进行配送。因此,这里的直送就是指商品直接从工厂送到需求地,配送是指暂存中转商品再将产品送至需求地。

首先我们假设生产工厂、消费地、集配中心在同一直线上,我么可以将直送与配送问题转换成:确定工厂的直送范围和配送中心的配送范围,从运输成本角度出发,设置为限制因素,构建分析模型,求得最优配送区域。

设:

K—生产工厂与集配中心的距离;

A—生产工厂与消费地单位重量、距离运价;

B—生产工厂至集配中心单位重量、距离运价;

C—集配中心至消费地单位重量、距离运价;

D—集配中心固定成本。

在这里我们考虑为了达到规模经济,生产工厂一般运往集配中心常采用大型车辆,集配中心运往消费地,由于运量的限制,往往采用小型车辆,我们假设B为大型车辆单位重量、距离的运价,C为大型车辆单位重量、距离的运价,一般情况下,B是小于C。D为集配中心单位重量产品所需的固定成本。

要解决这个问题,我们需要确定一个临界点,即:该点为生产工厂直送和转运至集配中心配送的成本分界。在这里我们假设成本的临界点离工厂距离为X,如图1所示。

在成本临界点分别讨论生产工厂直接送至消费地的方式和转运至集配中心再运送至消费地的运输成本的区别。

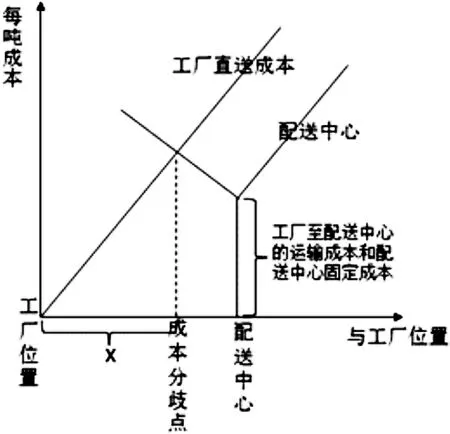
图1 直送配送运输成本

我们可以得到:

生产工厂直送至消费地运输成本为:AX

转运集配中心再配送的运输成本为:BK＋D＋(K－X)C

因为X是直送与配送的成本临界点,因此可以得到:AX＝BK＋D＋(K－X)C

至此,我们可以得到运输成本临界点X。

2.2 平面上运输成本临界线的确定

在这里拓展到实际情况,将生产工厂、消费地、集配中心至于同一平面上,临界点拓展至临界线,在这里我们需要确定运输成本的临界线,采用相同原理我们构建了三者之间的空间位置关系,如图2所示。

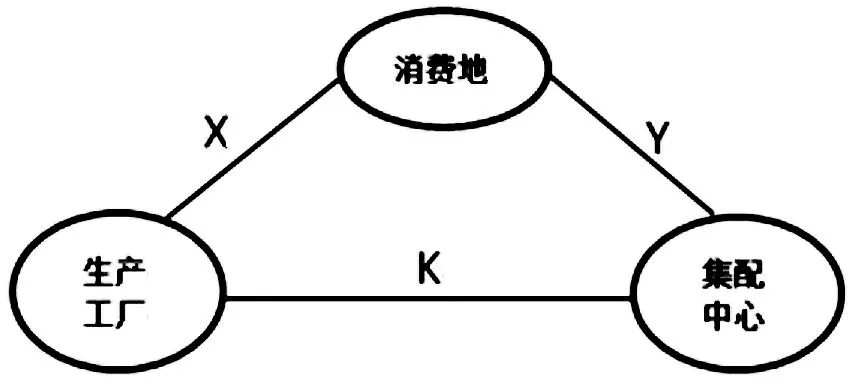
图2 配送直送平面图

设:

K—生产工厂与集配中心的距离;

A—生产工厂至消费地单位重量、距离运价;

X—生产工厂至消费地的距离;

E—生产工厂直送时的固定成本;

C—集配中心到消费地单位重量、距离运价;

Y—集配中心到消费地的距离;

D—集配中心配送时的固定成本(包括生产工厂到集配中心的运输成本)。

假设A＝C＝N,即在生产工厂和集配中心采用相同车型配送。则

生产工厂直送方式运输成本G＝AX＋E,

转运集配中心配送方式运输成本:H＝CY＋D,

在运输成本临界线上,有G＝H,

至此,D、E、N均为常数,我们可以得到X－Y也是一个常数,所以运输成本临界线可以得到为一条双曲线,双曲线的内侧是集散中心的配送区域,外侧是生产工厂直送区域。如图3所示。

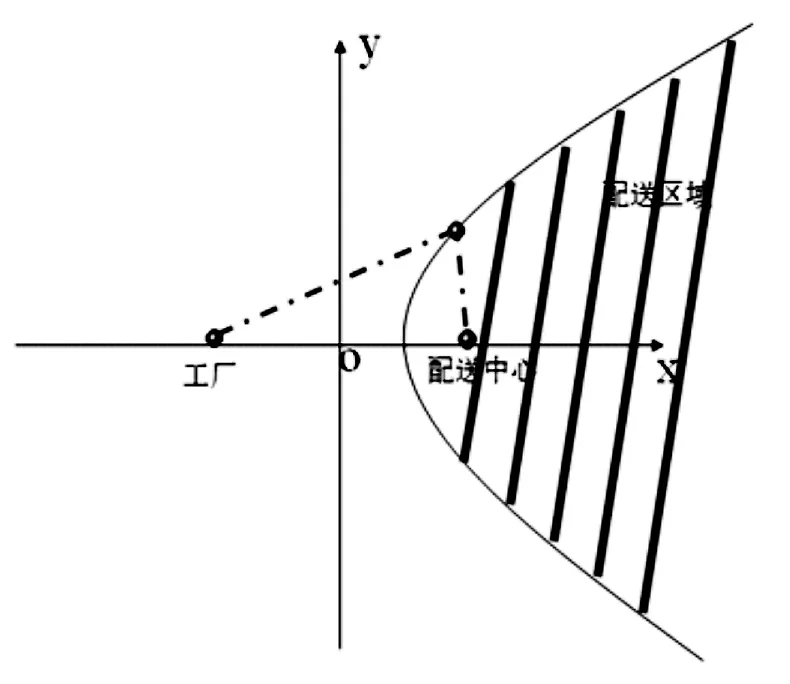
图3 直送配送区域

设生产工厂位置为(－K/2,0),(K为焦点),集配中心的位置为(K/2,0),则分界线为:

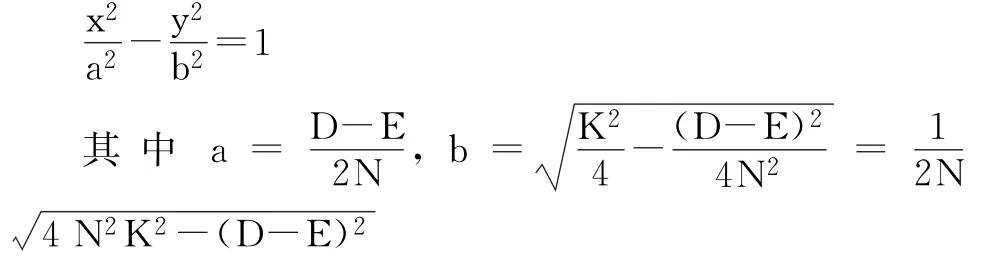
故工厂与配送中心最佳配送分界线的标准方程为:

2.3 多工厂多配送中心模型构建

2.3.1 一个工厂两个配送中心模型构建

以上为1∶1型,即一个工厂和一个配送中心的情况下配送与直送范围的界定,那么我们要推广到n∶n型,首先考虑的是增加一个配送中心,将模型拓展到1∶2型,并确定工厂、1号配送中心配送范围、2号配送中心配送范围。如图5所示。

(1)假设工厂、1号配送中心、2号配送中心在一条直线上。区域规划,如图6所示。

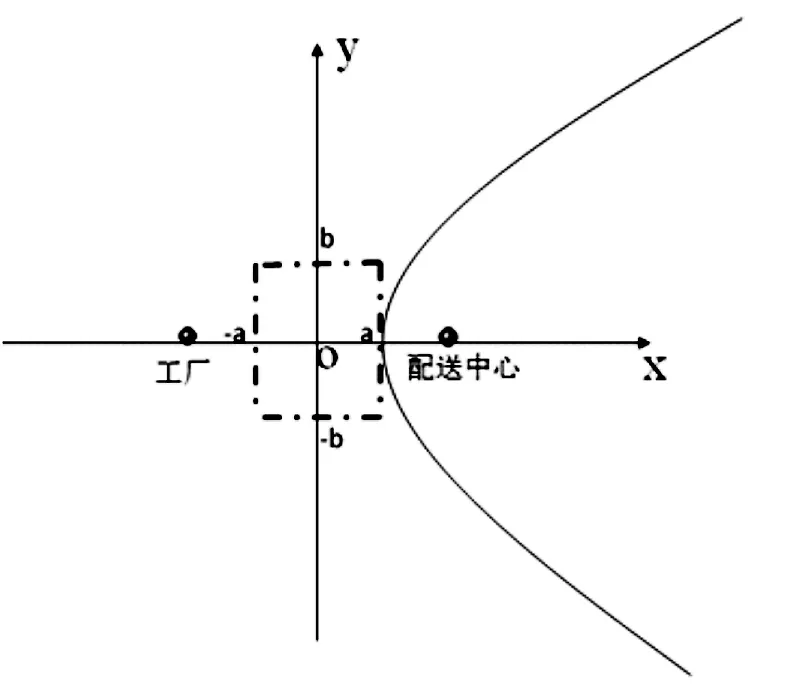
图4 双曲线结构

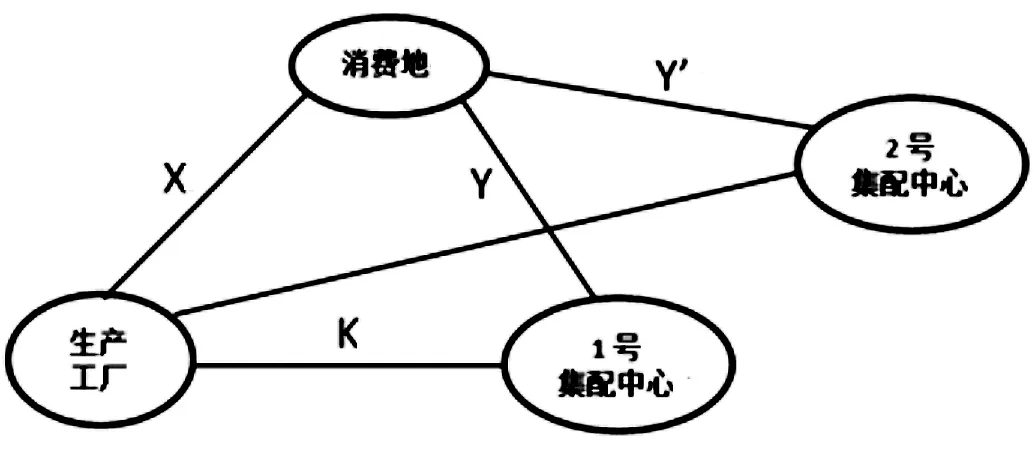
图5 配送直送平面图

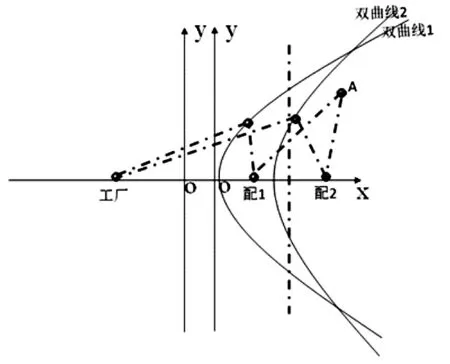
图6 配送、直送图

设:

A—生产工厂至消费地单位重量、距离运价;

X—生产工厂至消费地的距离;

E—生产工厂直送时的固定成本;

C—1号集配中心到消费地单位重量、距离运价;

Y—1号集配中心到消费地的距离;

D—1号集配中心配送时的固定成本(包括生产工厂到集配中心的运输成本)。

C′—2号集配中心到消费地单位重量、距离运价;

Y′—2号集配中心到消费地的距离;

D—2号集配中心配送时的固定成本(包括生产工厂到集配中心的运输成本)。

假设A＝C＝C′＝N,即在生产工厂、1号集配中心和2号集配中心均采用相同车型配送,且假设集配中心固定成本相同。

生产工厂直送方式运输成本G＝AX＋E,

1号集配中心配送方式运输成本:H＝CY＋D,

1号集配中心配送方式运输成本:H′＝C′Y′＋D,

双曲线1:

在运输成本临界线上,有G＝H,

双曲线1:

在运输成本临界线上,有G＝H′,

那么此时以两个集配中心作垂直平分线,可知:A点,在双曲线的内侧,则采用配送中心配送。

1号集配中心运输成本:H＝CY＋D,

2号集配中心运输成本:H＝C′Y′＋D,

由于A点在垂直平分线右侧,Y＞Y′,则H＞H′,故采用2号集配中心配送。

得到生产工厂直送范围与集配送中心配送范围,其中垂直平分线与双曲域1构成的区域采用1号集配中心配送,其中垂直平分线与双曲域2构成的右侧区域采用2号集配中心配送如图7所示。

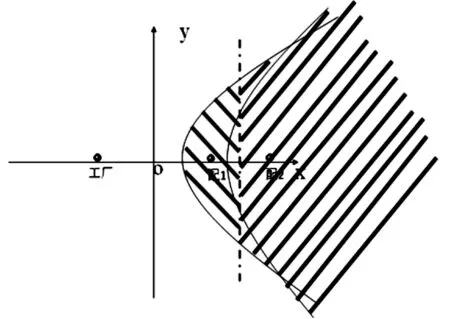
图7 工厂直送范围与配送中心配送范围

(2)假设工厂、1号配送中心、2号配送中心在任意位置。区域规划,如图8所示。

图8 工厂直送范围与配送中心配送范围

设:

A—生产工厂至消费地单位重量、距离运价;

X—生产工厂至消费地的距离;

E—生产工厂直送时的固定成本;

C—1号集配中心到消费地单位重量、距离运价;

Y—1号集配中心到消费地的距离;

D—1号集配中心配送时的固定成本(包括生产工厂到集配中心的运输成本)。

C′—2号集配中心到消费地单位重量、距离运价;

Y′—2号集配中心到消费地的距离;

D—2号集配中心配送时的固定成本(包括生产工厂到集配中心的运输成本)。

假设A＝C＝C′＝N,即在生产工厂、1号集配中心和2号集配中心均采用相同车型配送,且假设集配中心固定成本相同。

生产工厂直送方式运输成本G＝AX＋E,

1号集配中心配送方式运输成本:H＝CY＋D,

1号集配中心配送方式运输成本:H′＝C′Y′＋D,

双曲线1:

在运输成本临界线上,有G＝H,

双曲线1:

在运输成本临界线上,有G＝H′,

那么此时以两个集配中心作垂直平分线,可知:A点,在双曲线的内侧,则采用配送中心配送。

1号集配中心运输成本:H＝CY＋D,

2号集配中心运输成本:H＝C′Y′＋D,

由于A点在垂直平分线右侧,Y＞Y′,则H＞H′,故采用2号集配中心配送。

得到生产工厂直送范围与集配送中心配送范围,其中垂直平分线与双曲域1构成的区域采用1号集配中心配送,其中垂直平分线与双曲域2构成的右侧区域采用2号集配中心配送如图9所示。

图9 工厂直送范围与配送中心配送范围

实际情况下,不同配送中心固定成本不一样,假设距离工厂越远的配送中心固定成本越高,将(1)中情况进行变换。

设:

A—生产工厂至消费地单位重量、距离运价;

X—生产工厂至消费地的距离;

E—生产工厂直送时的固定成本;

C—1号集配中心到消费地单位重量、距离运价;

Y—1号集配中心到消费地的距离;

D—1号集配中心配送时的固定成本(包括生产工厂到集配中心的运输成本)。

C′—2号集配中心到消费地单位重量、距离运价;

Y′—2号集配中心到消费地的距离;

D′—2号集配中心配送时的固定成本(包括生产工厂到集配中心的运输成本)。

假设A＝C＝C′＝N,即在生产工厂、1号集配中心和2号集配中心均采用相同车型配送,且假设集配中心固定成本相同。

生产工厂直送方式运输成本G＝AX＋E,

1号集配中心配送方式运输成本:H＝CY＋D,

1号集配中心配送方式运输成本:H′＝C′Y′＋D′,

此时,以两个集配中心为焦点,再次构建一个双曲线3:

1号集配中心运输成本:H＝CY＋D,

2号配送方式费用:H′＝C′Y′＋D′,

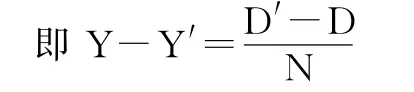
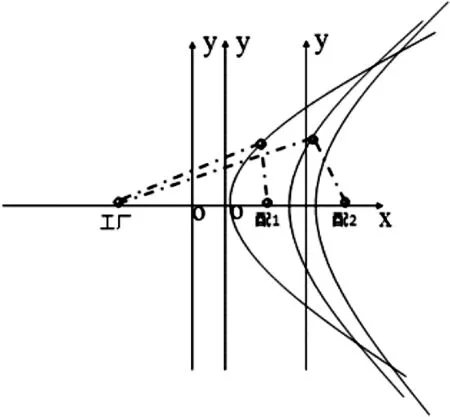
图10 工厂直送范围与配送中心配送范围

修改后的生产工厂直送范围与集配中心配送范围如图11所示,其中,左侧区域为1号集配中心配送区域,右侧区域为2号集配中心配送区域。

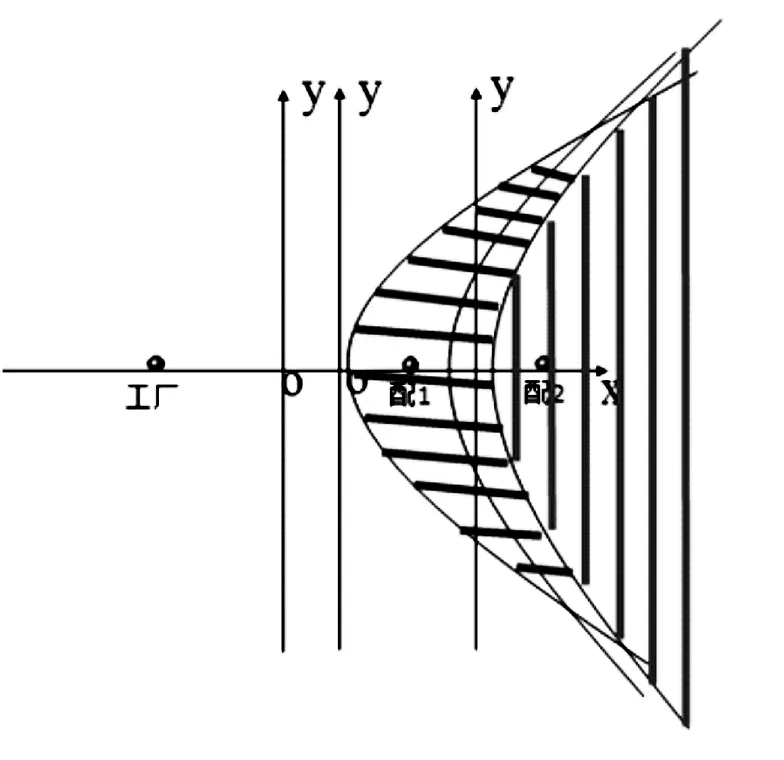
图11 工厂直送范围与配送中心配送范围

到此为止,采用相同理论方法可解决1∶n型,即一个工厂n个配送中心的问题。

2.3.2 两个工厂一个配送中心模型构建

此时,考虑增加一个工厂,将模型拓展到2∶1型。并确定1号工厂,2号工厂,配送中心配送范围。如图12所示。

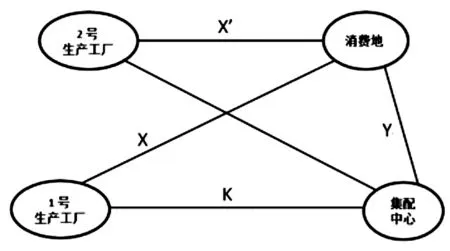
图12 多工厂单配送中心示意图

设:

A—生产工厂至消费地单位重量、距离运价;

X—1号生产工厂至消费地的距离;

X′—2号生产工厂至消费地的距离;

E—生产工厂直送时的固定成本;

C—集配中心到消费地单位重量、距离运价;

Y—集配中心到消费地的距离;

D—集配中心配送时的固定成本(包括生产工厂到集配中心的运输成本)。

假设A＝C＝N,即在1号生产工厂、2号生产工厂和集配中心均采用相同车型配送。

1号生产工厂直送方式运输成本G＝AX＋E,

2号生产工厂直送方式运输成本G′＝AX′＋E,

集配中心配送方式运输成本:H＝CY＋D,

双曲线1:

在运输成本临界线上,有G＝H,

双曲线2:

在运输成本临界线上,有G′＝H,

区域规划,如图13所示。

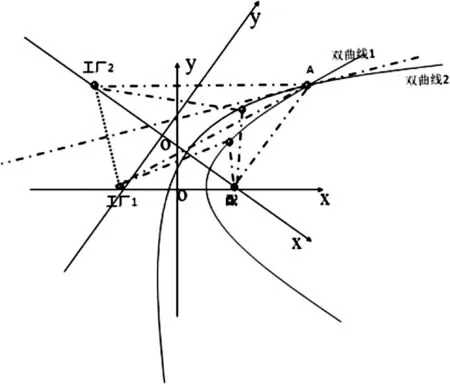
图13 多工厂单配送中心配送区域构建

那么此时以两个工厂作垂直平分线,讨论两个地方采

用什么配送方式。

(1)双曲线1与双曲线2所交区域。区域规划,如图14所示。

1号生产工厂直送方式费用:G＝AX＋E,

2号生产工厂直送方式费用:G′＝AX′＋E,

集配中心费用:H＝CY＋D,

此时,由于A点位于垂直平分线的右侧,则G＜G′;

A点位于双曲线1的外侧,则G＜H;

A点位于双曲线2的内侧,则H＜G′;

则G＜H＜G′,此时采用生产工厂1直送。

(2)双曲线1与垂直平分线所交区域

区域规划,如图15所示。

1号生产工厂直送方式费用:G＝AX＋E,

2号生产工厂直送方式费用:G′＝AX′＋E,

图14 多工厂单配送中心配送区域构建

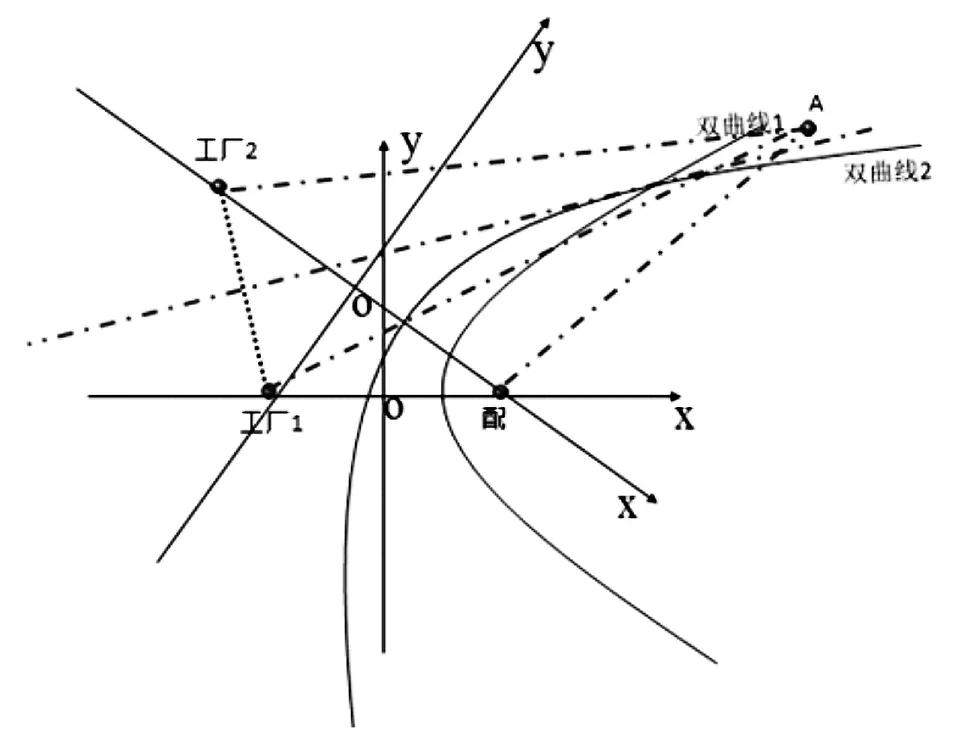
图15 多工厂单配送中心配送区域构建

集配中心费用:H＝CY＋D,

此时,由于A点位于垂直平分线的左侧,则G′＜G,

A点位于双曲线1的内侧,则H＜G,

A点位于双曲线2的外侧,则G′＜H,

则G′＜H＜G,此时采用工厂2直送。

得到工厂直送范围与配送中心配送范围如图16所示。

图16 工厂直送范围与配送中心配送范围

到此为止,采用相同理论方法可解决n∶1型,即n个工厂1个配送中心的问题,最终可拓展至n∶n型,解决任意多工厂与配送中心直送与配送问题。

3 结语

本文通过对直送和配送中的运输成本进行分析,建立成本约束公式,基于线性规划的方法,构建直送与配送区域划分模型。以一个配送中心、一个工厂的模式引入双曲线模型,划分出直送配送区域,并在此基础上,增加一个工厂,一个配送中心,采用相同理论方法,检验模型的可行性,并确定最优区域划分,以实现经济效益。本模型的进一步拓展方向为:在1∶2和2∶1模型的基础上拓展至n∶n型,解决一般性的直送配送区域划分问题。

[1]中国物流交易中心.电商知识平台[EB/OL].http://www.56135.com/56135/info/infoview/108573.html,2014.

[2]孙焰.现代物流管理技术—建模理论及算法设计[M].上海:同济大学出版社,2004,(8):1-5.

[3]宋世强.物流运输管理决策优化问题研究[D].南昌:江西财经大学,2006.

[4]杨家其.现代物流与运输[M].北京:人民交通出版社,2003,(5).

[5]胡列格.物流运筹学[M].北京:电子工业出版社,2005,(8).