植被微波遥感下粒子的散射特性研究

广东理工学院 李欣雪 邓超兵 张晓亚 龙小丽

植被微波遥感下粒子的散射特性研究

广东理工学院 李欣雪 邓超兵 张晓亚 龙小丽

植被微波遥感下粒子学研究，是研究植被产量的重中之重。植被的内部结构的散射，可以看成是多个形状粒子叠加而成。本文水平极化方式、垂直极化方式下，对盘状、针状、椭球状散射粒子的散射系数进行模拟，选取了两种波段（S波段和C波段）分别进行分析。

微波遥感；粒子；极化方式；后向散射系数

0 引言

农作物的产量是一个国家得以发展的前提，关系到社会的安全稳定。我国有13亿人口，是全世界人口总数最多的国家，但农作物的耕地区域却只占全世界的7%，人均约只占全球平均耕地面积的33%。提高作物的产量是我国发展的重中之重，长久以来得到人民的广泛关注。使用微波遥感对其生长情况进行实时监测分析，对产量的估计起到至关重要的作用。因此对于微波遥感技术下植被粒子的散射特性研究是我们研究的重要方向。

在研究植被的散射，不仅要考虑土壤的散射，而且也要考虑植被层的散射[1]。当农作物长势相对茂盛时，我们还需思虑到他们自身的相互作用，农作物与地面之间的多次散射的作用，这样才较全面分析了有关植被散射的相关问题[2]。

1 任意形状粒子的散射场

设在多叶的半空间植被模型，包括任意角度任意形状的介质散射体。此模型被选择为研究叶片散射[3]。设入射的平面波为：

其中，k是背景介质的波数；i是入射方向，q为v或h，分别为垂直极化和水平极化。而经欧拉角进行旋转可得出不同角度下的旋转坐标系，从而可以得到植被枝干、叶片不同的取向，其中本文的欧拉角旋转取向如图1所示。

图1 欧拉角的取向

农作物的结构通常可分为几部分，如茎、叶等，通常被模拟为的单个散射粒子。我们常见的散射粒子模型有：有限长介质圆柱体模型；球形瑞利粒子模型；瑞利近似下的非球形粒子模型；广义瑞利金斯（GRG）类似下的盘状或针状的散射模型等。

对于散射场的一般公式可以通过Helmholtz的积分方程得到。对于位于原点的散射，惠更斯方程，从远区散射场近似得到近区散射场的相关方程[4]，如下：

在公式中，在计算中的主要任务是估计的内场，广义Rayleigh-Gans估计的内场适用于非常小的散射。瑞利金斯近似的估计适用于薄膜散射，广义瑞利金斯适用于与一个尺寸较小波长相比的非薄膜散射。通常情况下，可用无限长的圆柱散射体的内场，看作是有限长圆柱散射体的内场。而相对于扁薄的散射体，可用相同厚度的介质平板的场来近似的看作是该散射体的内场。

2 盘状、针状散射粒子

对于平面波，内薄散（磁盘和针状）场用广义瑞利金斯（GRG）近似估计。这导致了散射幅度张量等于经由瑞利近似（偶极子术语）与修正函数获得。

对于具有对称性的z轴的散射，与入射场的波长相比尺寸小的一个或两个，使得，D是最小尺寸，我们可以估算散射体作为内部的磁场[5]。

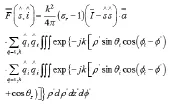
它的计算结果依赖于两个因素，分别是几何体形状和修正函数、去磁因子的数量。在下面的章节中，我们将讨论圆盘散射体和针状散射体的去磁因子和修正函数，其中修正函数也成为Debye干涉因子。

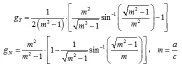
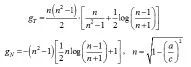
3 椭球散射粒子

相比于盘状，针状粒子，椭圆球粒子最大的区别就在于去磁因子的计算。当中计算椭球形散射体时，即时，去磁因子的公式可以表示为：

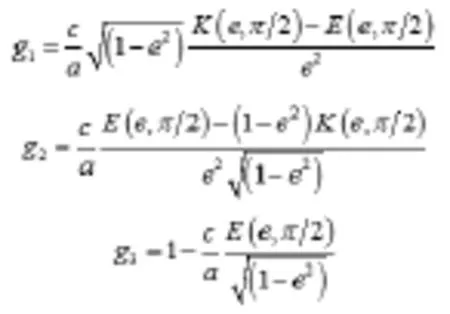
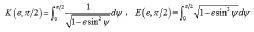
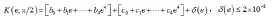
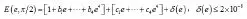
4 后向散射计算及分析

在微波定量遥感中，后向散射系数是经常会去计算的量，对线极化波，表达式如下[6]：

对于圆极化波散射系数计算有：

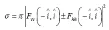
该式子中的“十”和“一”分别代表电场的左旋和右旋。当选取左手放入电场中，除拇指外，四指弯曲，此时大拇指的指向是波的传播方向，其余手指指向是电场矢量的端点运动的方向，符合这种情况叫做左旋极化波；同样，改用右手去重复上面的动作时，符合右旋情况，则被叫做右旋极化波。

通过计算推导，模拟出图2（左）到图3（右），分别给出S波段(3.2GHz)和C波段(6.75GHz)，在同极化、交叉极化的后向散射系数和角度变化的变化。实验结果如下：

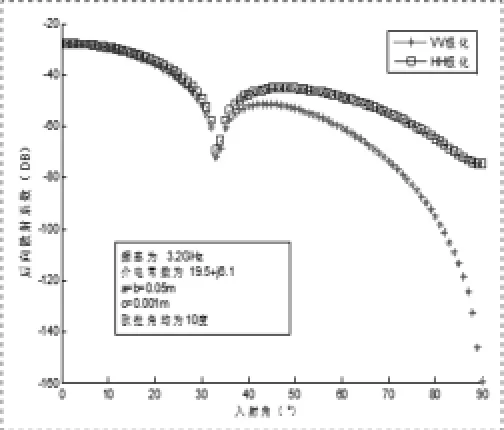
图2 S波段圆盘状散射体的变化曲线图

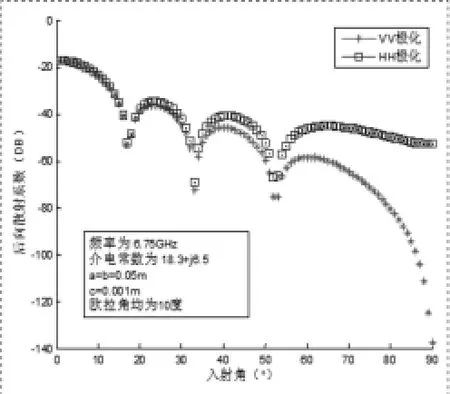
图3 C波段圆盘状散射体的变化曲线

图2和图3是圆盘在S波段和C波段的散射示意图，表示出了其系数随着入射角的变化而波动的曲线。我们可以从两个图中看出，入射波频率的不断增大时，后向散射系数在0度到90度有规律的进行变化，其峰值的个数在不断的变多，但是峰值在不断变小。在图中我们同样可以发现，其HH极化参数要比VV极化的参数值大，产生这种情况的原因是由于盘状散射体的水平极化的散射比垂直极化的散射强。

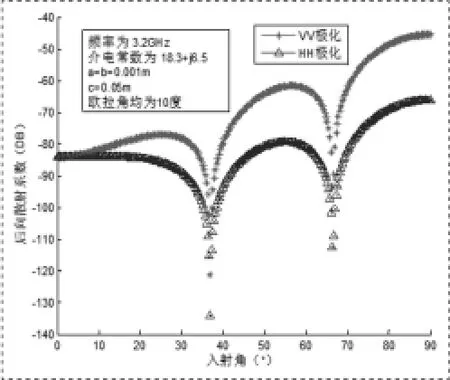
图4 S波段针状后向散射系数的变化曲线

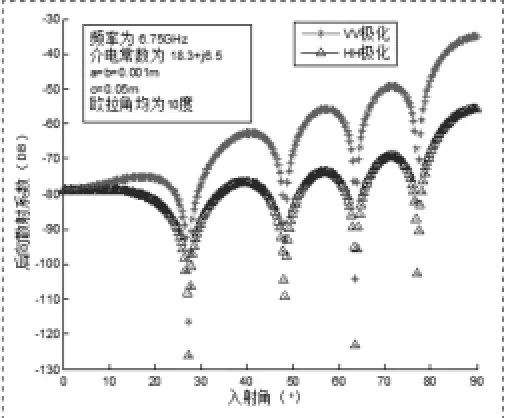
图5 C波段针状后向散射系数的变化曲线

图4和图5给出了在入射角0度到90度之间，针状散射体在S波段和C波段的后向散射系数的波动曲线。从图中能看出，针状与圆盘状散射体有着同样的趋势，曲线的峰值个数随着频率的升高而逐渐升高。但是与圆盘状散射体不同的是，对于针状散射体，其VV极化大于HH极化，这是由于针状的几何形状的尺寸，VV极化的散射较强。

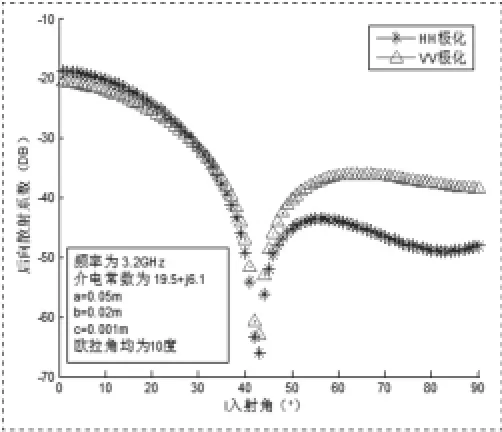
图6 S波段椭圆球散射体后向散射系数变化曲线

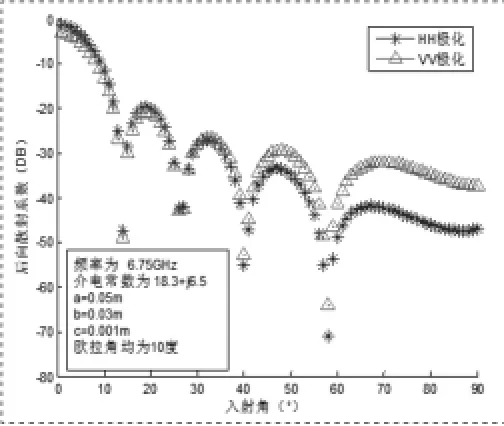
图7 C波段椭圆球散射体后向散射 系数变化曲线

图6和图7给出了入射角度在90度内变化，椭球状在S波段和C波段的后向散射系数随角度的波动趋势。在S波段（图3-7）中能看出，椭球状的散射体的VV极化先是比HH极化大，而当角度增高到某个值时VV极化又比HH极化小。发生这种情况的原因是椭球散射体的几何尺寸在圆盘状和针状内，所以才会呈现出此种散射特征。同理我们也能在C波段（图3-8）中看出同样的规律。

5 总结

在对后向散射系数的模拟中，运用广义瑞利金斯（GRG)）计算方法，用无限长的内场估计有限长的内场的方法对单个粒子的电磁散射特性进行分析。经模拟计算研究看出，对于圆盘粒子的场而言，不同波段的结果都呈现HH极化的值都要高于VV极化的值，这是因为圆盘状散射体对于水平极化的散射比垂直极化强；而对于针状散射体而言则正好相反，其VV极化要大于HH极化散射结果，主要由于针状散射体对垂直极化的散射比水平极化强。此外，无论对于何种形状的散射体，其后向散射系数在0度到90度之间的有规律变化的峰值数目随着频率升高而增加。

[1]L.E.Pierce,M.C.Dobson,E.P.Wilcox,et al.Artificial neural network inversion of tree canopy parameters in the presence of diversity[J]. Geoscience and Remote Sensing Symposium.1993,2(11):394-397.

[2]F.T.Ulaby,M.Razani,and M.C.Dobson.Effects of Vegetation Cover on the Microwave Radiometric Sensitivity to Soil Moisture[J]. IEEE Transactions on Geoscience and Remote Sensing.1983,21(1):51-61.

[3]M.A.Karam and A.K.Fung.Leaf-shape effects in electromagnetic wave scattering from vegetation," IEEE transactions on geoscience and remote sensing [J].1989,27(26):687-697.

[4]Karam M.A.,Fung A.K.and Antar Y.M.M.Electromagnetic Wave Scattering from Some Vegetation Sample[J].IEEE Transactions on Geoscience and Remote Sensing.1988,26(6):799-808.

[5]R.Schiffer and K.O.Thielheim.Light scattering by dielectric needles and disks[J].J.Appl.Phys.1979,50(4):2476-2483.

[6]金亚秋.电磁散射和热辐射的遥感理论[M].科学出版社,1993:25-30.

李欣雪【通讯作者】（1990—），女，黑龙江大庆人，硕士研究生，助教，研究方向：电子与通信工程。

邓超兵（1988—），男，湖南邵阳人，硕士研究生，助教，研究方向：控制科学与工程。

张晓亚（1987—），女，河南漯河人，硕士研究生，助教，研究方向：复杂过程工业故障诊断。

龙小丽（1989—），女，湖南湘西人，硕士研究生，助教，研究方向：电子与通信工程。