双源超声辅助铸造相位差对铝合金细晶效果的影响

章武，李晓谦，彭浩，蒋日鹏



双源超声辅助铸造相位差对铝合金细晶效果的影响

章武，李晓谦，彭浩，蒋日鹏

(中南大学轻合金研究院，高性能复杂制造国家重点实验室，长沙 410083)

建立双源超声铝合金铸造熔池模型，利用fluent软件模拟相同频率与不同频率下相位差对熔池声场的影响。仿真结果显示，相同频率下，相位差显著影响熔池声场的分布，随相位差增大，熔池空化域变小；不同频率下，相位差对熔池声场的分布无影响。通过不同相位差双源超声铸造试验发现，同频率振动下，相位差对双源超声铸造边部及超声辐射区的晶粒细化效果影响很小，心部晶粒细化效果随相位差变大效果变差；不同振动频率作用下，相位差对铸锭细晶效果无影响，心部晶粒细化效果与同频率相位差为90°时接近。同频率相位差0°超声作用下，铸锭心部晶粒尺寸较常规不同频率双源超声作用下心部晶粒尺寸大幅减小。

铝合金；双源超声铸造；相位差；空化域；晶粒细化

超声铸造是一种无污染、高效率且极具发展潜力的新型铸造技术。目前的研究认为，超声波在熔体中产生的空化效应能显著细化晶粒，提高材料性能，在强超声场正负声压的高频交替作用下，形成空化泡，空化泡崩溃瞬间产生的高温高压以及高强度的微射流，促使铝合金熔体中的初生晶被打碎，异质结晶核数目增多，结晶核与固相间的润湿角被减小，实际结晶温度降低，过冷度增大，从而使凝固组织得到明显的细化[1−5]。由于铝合金熔池的高温，高腐蚀性，不可见及金属屏蔽作用，鲜有有效的设备来检测铝熔体中的超声波声场分布，故采用数学模拟的方法对铝熔体中超声声场的分布进行研究。目前，对多源超声铸造的研究都是基于单个超声源，不考虑多个超声源之间的相位差，对多个超声源之间的相互协同叠加作用鲜有涉及。对于大规格铸锭的超声铸造，由于铸锭半径增大，为改善大铸锭整体材料性能，一般采用导入多个超声源的方法，例如630 mm圆锭超声铸造导入两个超声波源[6−9]，多个超声源产生的超声波在铝熔体中传播时，波与波之间存在叠加效应，波的叠加会影响到熔池中的声场分布，影响超声空化域分布，从而影响超声铸造铸锭的铸造效果，而波与波的叠加与振动相位差相关[10−11]。目前的研究基本没有涉及相位差对双源超声铸造的影响。本文应用fluent软件对双超声波源的超声铸造声场分布与振动相位差的关系进行了研究，并搭建试验平台对模拟结果进行验证，探讨双源超声铸造时相位差对铸造效果的影响，为双源超声铸造两个超声源之间的工艺参数匹配提供理论依据。

1 双源超声熔池声场数值模拟

1.1 模型与参数

图1(a)所示为铝合金圆锭铸造现场图，在630 mm铝合金圆锭半连续铸造中，对称布置两套波振动系统，超声波通过垂直浸入铝液中的超声辐射杆直接导入熔体中，实测得熔池深度为450 mm，辐射杆间中心距离为180 mm。

图1(b)所示为仿真模型，考虑到铸造工艺条件的对称性，取1/2熔池为计算域，辐射杆端面振幅分布均匀[12]，利用fluent 动网格技术通过超声辐射杆端面导入超声振动，采用vof模型模拟铝液与空气分界处的自由面，以熔池液面中心为计算域原点，辐射杆端面中心坐标分别为(−90，0，240)和(90，0，240)，底面及侧面边界为刚性硬壁面，熔池上与空气接触液面为自由液面，空气层上表面为压力无限远程边界，熔池温度为720℃，辐射杆振幅为12 μm，施振频率采用目前超声铸造常用频率，分别为19，20和20.5 kHz，采用六面体结构单位划分网格，计算过程为瞬态，时间步长为2.5×10−6s，计算20000步，模拟相位差对熔池声场分布的影响。

1.2 模拟结果与分析

仿真过程中发现相位差对熔池声场的影响与频率是否相同有关，故仿真结果按相同频率与不同频率来分析。

1.2.1 相同频率下相位差对声场分布的影响

施振频率为实验常用的20 kHZ，相位差分别为0°，45°，90°，135°，180°。已有研究表明铝熔体中发生超声空化效应的必要条件是声压幅值大于空化阈值1.1 MPa[13]，所以模拟结果选取声压大于1.1 MPa的空化域来分析，将一个振动周期均分取四个时间点，熔池中心对称面上空化域变化与相位差的关系如图2所示。

由图2可知，同频率下，在相位差为0°时，两个辐射杆超声的空化域同步增大，辐射杆之间存在明显的超声叠加增强作用，空化域接连在一起，明显增大，中心区域存在明显的空化区域；随相位差增大至45°，辐射杆振动稍有异步差，辐射杆之间仍存在叠加增强区域，空化域接连在一起，但其面积较相位差为0°时小；当相位差为90°及135°时，则不能观测到明显的叠加增强区域；当相位差为180°时，超声振动完全异步，一个振动周期内，一个辐射杆产生正声压时，则另一辐射杆产生负声压，各自产生空化时间异步，空化域向熔池外侧偏移，靠近熔池中心线侧空化域减小。这是因为，一辐射杆产生的负声压与另一辐射杆产生的正声压抵消，使得总声压减弱，因此相位差为180°时，两辐射杆产生的空化效果变弱。可以推测，频率相同时，0°相位差的空化域最大，超声铸造效果最好，铸锭心部晶粒细化效果好，随相位差增大，空化域减小，铸造效果变差，铸锭心部晶粒细化效果变差。

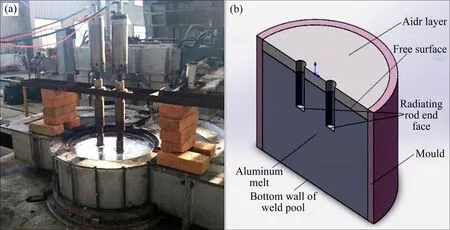
图1 铝合金双源超声铸造熔池声场模拟模型

图2 同频率不同相位差双源超声铸造熔池空化域变化的时间历程

1.2.2 不同频率下相位差对声场分布的影响

仿真选取19 kHz与20.5 kHz两个铸造常用频率。在不同频率下，由于难以观测到空化域变化规律，故采用监测点的方式，提取不同方位8个监测点的声压随时间变化的波形图，发现各个点的声压幅值不恒定，幅值的包络线为一有固定波结的周期变化曲线，以熔池中心线上距辐射杆端面下方5cm处为例。图3 所示为不同频率双源超声铸造心部声压波形与相位差的关系，由图3可知，当超声频率不同时，熔池内某一点的声压幅值呈一波节的周期变化。对比图3中(a)，(b)，(c)，(d)可知，随相位差增大，熔池内某点的声压宏观曲线不发生变化，相位差只是改变该点声压的初始值，不影响整体声压变化，在不同频率下，相位差对双源超声铸造熔池内声场分布无影响。可以推测，在不同频率下，相位差对双源超声铸造效果无影响。

2 双源超声波铸造实验

2.1 实验材料与装置

7050铝合金，试验使用设备为铸造用超声波电源，铸造用超声振动系统(包含PZT压电陶瓷片，变幅杆，辐射杆)。其它辅助设备为井式加热炉，微米级基恩士激光测距仪，高精度电子称，石墨坩埚，热电偶，游标卡尺。

在同振动频率下，为达到控制振动相位差的目的，选取了两套同批次超声振动系统，并设计了如图4所示的电路。

超声振动系统驱动源来自上部的压电陶瓷组，压电陶瓷的振动相位与输入的电压相位一一对应，所以可以通过改变超声振动系统输入端的电压相位来改变超声振动系统的振动相位。图4(a)中两套相同的超声振动系统共用一个超声波电源，故其振动同步，相位差为0o；图4(b)中采用RC移相电路，RC移相电路能改变电压相位差，依式Δ=−tan−1()[14]，选取6 μF/ 450 V电容，20 Ω/100 W电阻，则相位差为86.3°；图4(c)中一套超声振动系统输入端反接，则相对另一套超声振动系统，其输入电压相位差为180°，因而振动相位差也为180°。

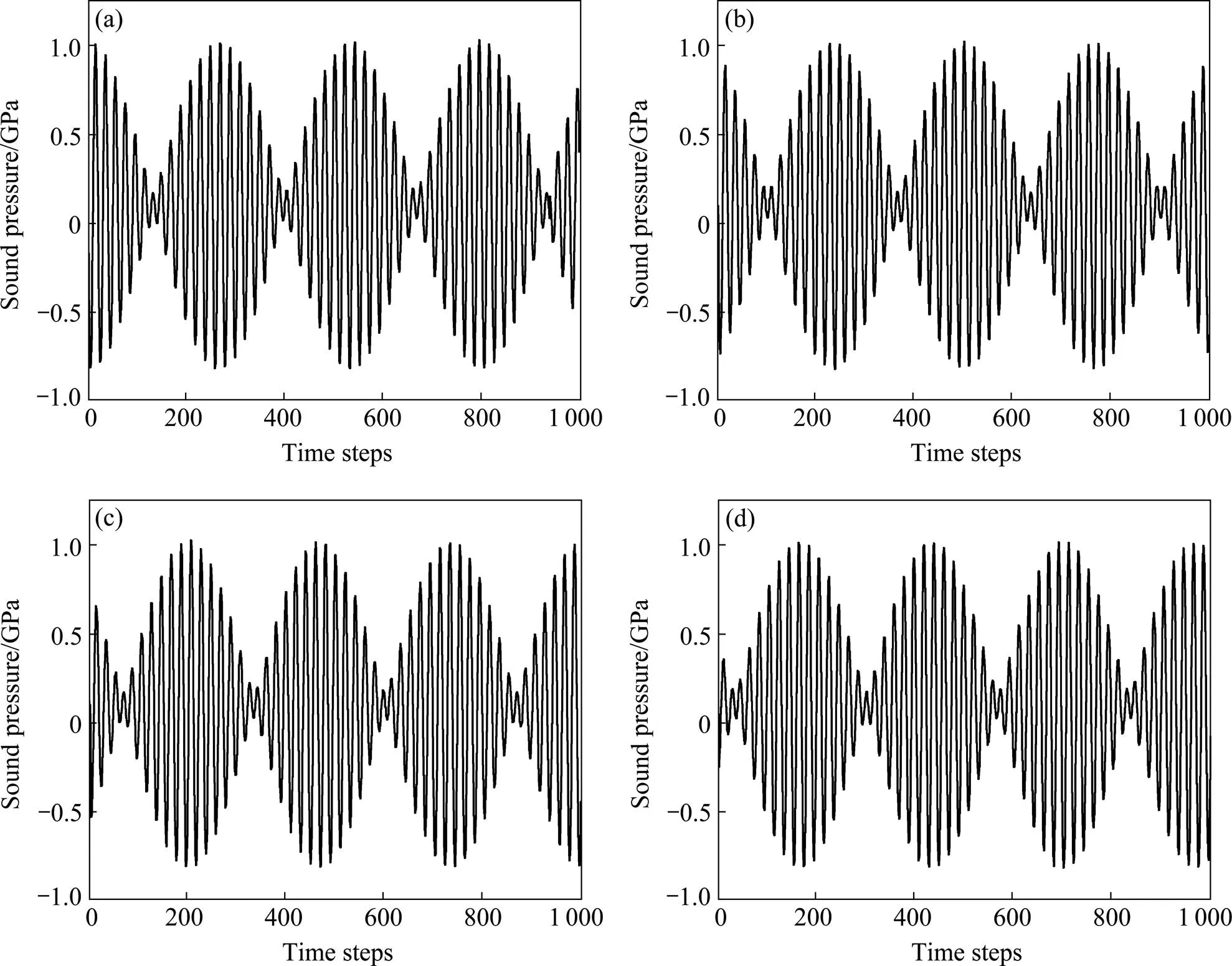
图3 不同频率双源超声铸造心部声压波形与相位差的关系

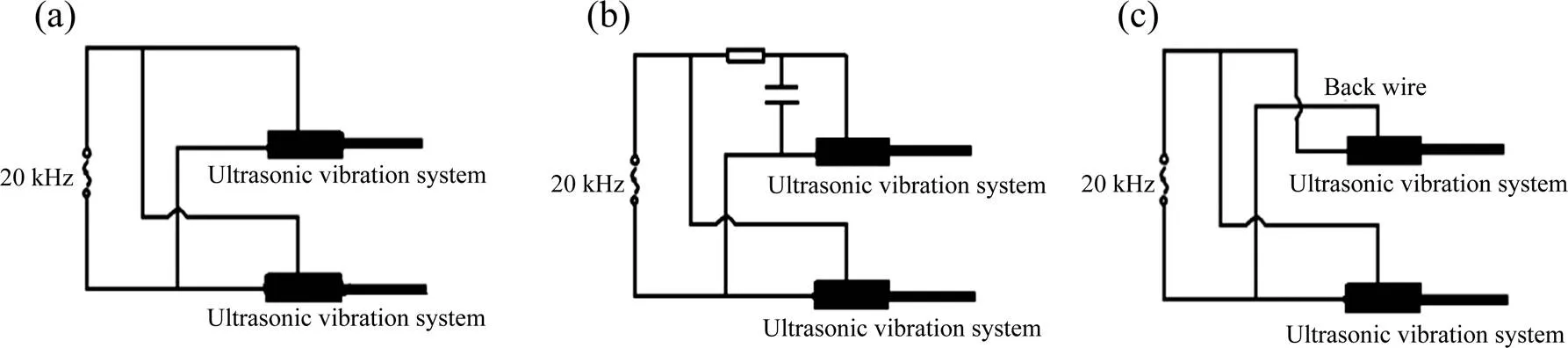
图4 同频率不同相位差超声振动系统装置原理图

在不同振动频率下，必须采用两套超声波电源，输入端相位差不可控，目前对高频微振动，很难测得其初始振动相位差，采用两套超声振动系统时，相位差与超声电源启动时间有关，因为超声为高频振动，周期为5×10−5s，在如此短时间内，很难控制超声电源启动时间，故本文只做随机相位实验。

2.2 实验过程及取样部位

为保证试验时辐射杆端面振幅一致，铸造实验前，用微米级基恩士激光测距仪对辐射杆端面振幅进行测试，调节超声波电源输出功率，使得辐射杆端面振幅保持在12 μm。铸造实验示意图如图5(a)所示，石墨坩埚尺寸为25cm，辐射杆距离中心10 cm。振动频率相同时，选取两套20 kHz超声振动系统，针对相位差为0°，86.3°及180°各做1组实验，而对不同振动频率，选取19.5 kHz及20.5 kHz两套超声振动系统，随机相位差做3组实验。

铸造结束后，在辐射杆端面下方5 cm处，按图5(b)取一条形样，从距离铸锭端部20 mm处开始，以20 mm为间距截取金相试样，通过金相显微镜观测微观组织，统计和计算出不同位置的晶粒尺寸。

2.3 实验结果与分析

图6所示为在同频率振动，不同振动相位差超声作用下，铸锭不同位置的微观组织。由图可知，超声铸造后，铸锭所有区域晶粒明显细化，不同相位差时，心部细晶效果差异较大。相位差为0°时，铸锭心部细晶效果显著，心部晶粒平均尺寸为140 μm，晶粒均为细小等轴晶；相位差为86.3°时，心部晶粒尺寸为186 μm，部分晶粒粗大不规则；而当相位差为180°时，心部晶粒平均尺寸为241 μm，且晶粒不规则，有发展成枝状晶的趋势。相位差越小，中心区域晶粒细化效果越好，对边部与超声辐射区晶粒细化效果差别不大。从前面的模拟结果可知，当相位差为0°时，由于超声辐射杆声压叠加增强，无论声压辐射区还是铸锭心部声压幅值较大，均出现空化效应，所以心部细化效果好；而随相位差增大，由于超声辐射杆产生的超声传至心部区域不同步，导致心部声压幅值反而降低，当相位差为180°时，则完全异步，心部声压正负抵消，导致铸锭心部超声幅值很低，心部区域晶粒细化效果差。因超声波在铝熔体中传播时存在衰减[15]，在边部及超声辐射区，一根超声辐射杆产生的超声波与另一辐射杆产生的超声波叠加后相对影响较小，其中一根辐射杆产生的超声波起主导作用，故而相位差对边部及超声辐射区细晶效果的影响较小。

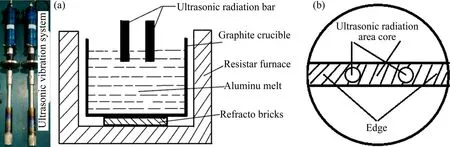
图5 双源超声波铸造示意图

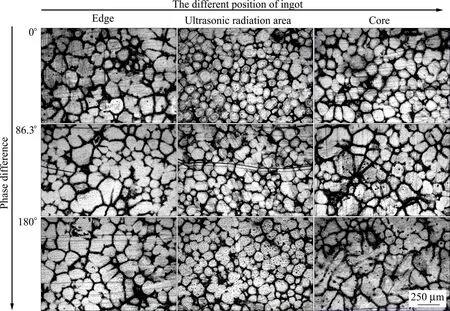
图6 同频率不同相位差双源超声铸造铸锭的微观组织

图7所示为不同振动频率下随机相位铸锭不同位置晶粒细化效果，由图可知，在不同频率下，相位差不同时，铸锭各位置细晶效果基本无差别，边部与超声辐射区的晶粒尺寸与同频率下边部和超声辐射区的晶粒尺寸基本相同，心部晶粒尺寸为197 μm，与同频率超声作用下相位差为86.3°时接近，较相位差为180°时细小。

同时在数十次630 mm圆锭双源超声铸造中，都是采用两套超声电源，各自控制一套超声振动系统，超声振动系统频率不同，相位差与超声电源启动时间有关，相位差随机变化，在数十次双源超声630 mm圆锭铸造后，观察圆锭微观组织，发现各个位置细晶效果差别不大[9]。结合前面仿真结果，可推测在不同频率双源超声铸造中，铸锭细晶效果与相位差无关。

从前面仿真结果可知，两个辐射杆频率不同时，相位差不影响熔池声场分布。熔池中各点声压波形为一存在波结的周期波动，在频率不同时，熔池中空化域变化可以近似看成一系列相位差在不停变化的同频率振动的组合，在熔池心部存在声压叠加增强时刻，也存在相互抵消削弱时刻；而在同频率超声振动相位差为0°时，心部声压始终增强，相位差为180°时声压始终削弱，故在不同频率超声作用下，心部晶粒细化效果较同频率超声振动0°相位差时差，与同频率超声振动相位差为90°时接近。相对目前双源超声铸造常采用不同振动频率的超声振动系统而言，相同频率，0°相位差的超声振动系统对心部晶粒细化效果更好。

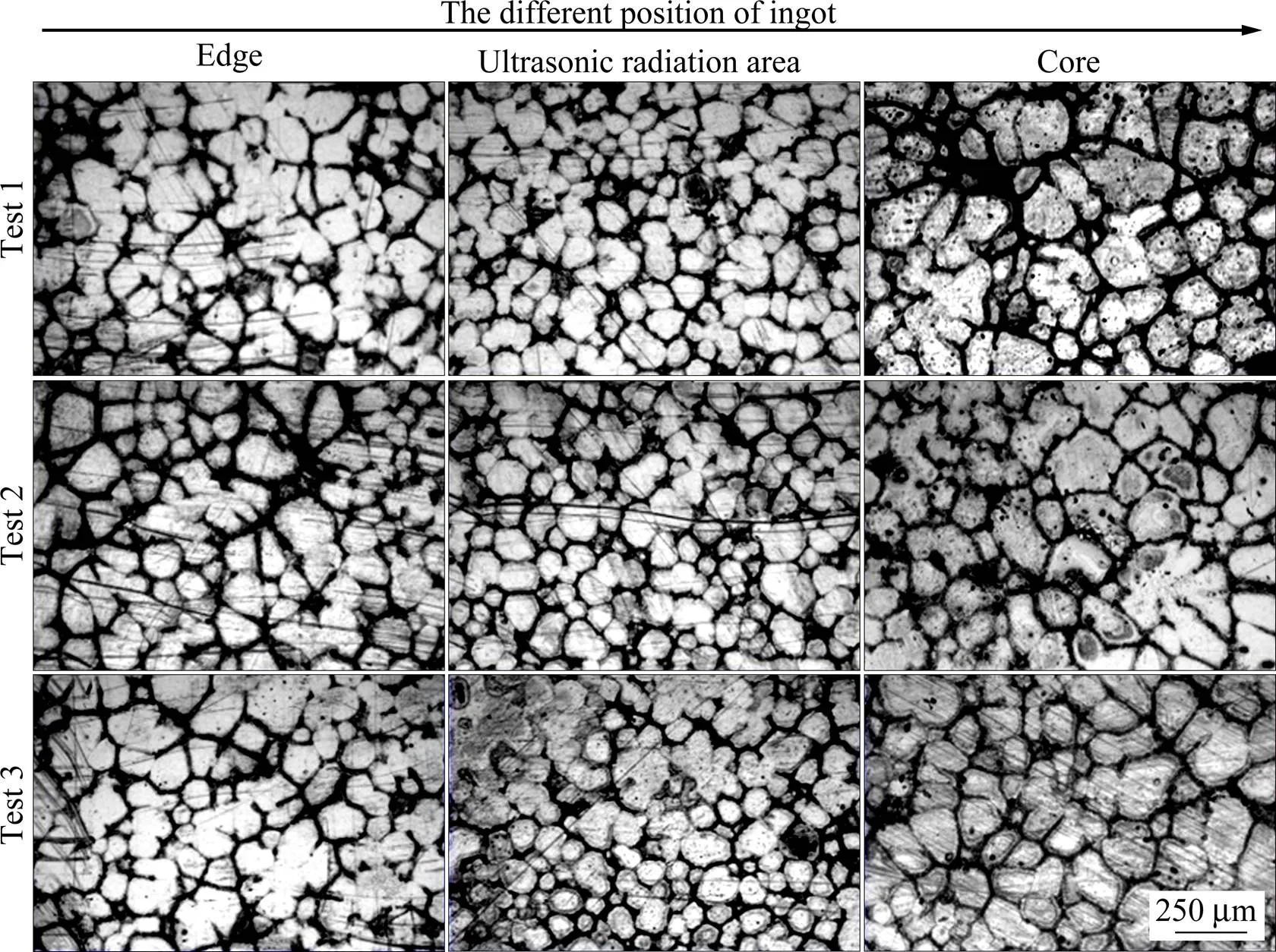
图7 不同频率双源超声铸造铸锭的微观组织

3 结论

1) 相位差对双源超声铸造熔池声场分布的影响与频率有关。频率相同时，相位差显著影响其声场分布，相位差为0°时，熔池空化域最大，随相位差增大，空化域减小；频率不同时，相位差对熔池声场分布无影响。

2) 同频率振动下，相位差对双源超声铸造边部及超声辐射区晶粒细化效果的影响很小，心部晶粒细化效果随相位差增大效果变差；不同振动频率作用下，相位差对铸锭细晶效果无影响，心部晶粒细化效果与同频率相位差为90°时接近。

3) 同频率0°相位差超声作用下，铸锭心部晶粒尺寸相对常规不同频率双源超声作用下心部晶粒尺寸大大减小。

[1] 冯若. 超声手册[M]. 南京: 南京大学出版社, 1999: 56−61.1999: 56−61. FENG Ruo.Ultrasound Handbook[M]. Nanjing:Nanjing University Press, 1999: 56−61.

[2] LAURENTIU N. Mathematical modeling of the solidication structure evolution in the presence of ultrasonic stirring[J]. Metall Mater Trans B: Process Metallurgy and Materials Processing Science, 2011, 42(6): 1297−1305.

[3] 黎正华, 李晓谦, 张明, 等. 超声外场7050铝合金铸锭凝固微观组织的影响[J]. 粉末冶金材料科学与工程, 2011, 16(3): 341−348. LI Zhenghua, LI Xiaoqian, ZHANG Ming, et al. Influence of ultrasonic field on solidification microstructure of 7050 aluminum alloy [J]. Materials Science and Engineering of Powder Metallurgy, 2011, 16(3): 341−348.

[4] NIE K B, WANG X J, WU K, et al. Effect of ultrasonic vibration and solution heat treatment on microstructures and tensile properties of AZ91 alloy[J]. Materials Science and Engineering A, 2011, 52(8): 7484−7487.

[5] 蒋日鹏, 李晓谦, 鞠增业. 铝合金超声波半连铸多场耦合的模拟与实验[J]. 华南理工大学学报: 自然科学版, 2014, 42(4): 85−90. JIANG Ripeng, LI Xiaoqian, JU Zengye, et al. simulation and experimental investigation of multi-field coupling for semi-continuous casting of aluminum alloy with ultrasonic treatment[J]. Journal of South China University of Technology: Natural Science Edition, 2014, 42(4): 85−90.

[6] HUANG Haijun, XU Yifan, SHU Da, et al. Effect of ultrasonic melt treatment on structure refinement of solidified high purity aluminum[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(7): 2414−2419.

[7] 张海澜. 理论声学[M]. 北京: 高等教育出版社, 2008: 125− 128. ZHANG Hainan.Theoretical Acoustics[M]. Beijing:Higher Education Press, 2008: 125−128.

[8] ESKIN G I. Ultrasonic Treatment of Light Alloy Melts[M]. CRC Press, 1998:41−51.

[9] YAN J C, Zhao W W, Xu H B, et al. Ultrasonic Brazing of Aluminum Alloy and Aluminum Matrix Composite[P]. US7,624,906,B2. 2009.

[10] DAS A, KOTADIA H R. Effect of high-intensity ultrasonic irradiation on the modification of solidification microstructure in a Si-rich hypoeutectic Al-Si alloy[J]. Materials Chemistry and Physics, 2011, 125(3): 853−859.

[11] LOUISNARD O. A simple model of ultrasound propagation in a cavitating liquid (Part I): Theory, nonlinear attenuation and traveling wave generation[J]. Ultrasonics Sonochemistry, 2012, 19(1): 56−65.

[12] 张敏, 李晓谦, 蒋日鹏, 等. 超声辐射杆振幅分布与空蚀区域[J]. 振动与冲击, 2014, 33(13): 59−62. ZHANG Min, LI Xiaoqian, JIANG Ripeng, et al. Amplitu-de distribution and cavitation corrosion field of ultrasonic transducer system[J]. Journal of Vibration and Shock, 2014, 33(13): 59−62.

[13] ESKIN G I. Broad prospects for commercial application ofthe ultrasonic (cavitation) melt treatment of light alloys[J]. Ultrasonics Sonochemistry, 2001, 8(3): 319−325.

[14] 孙克军. 电工手册[M]. 北京: 化学工业出版社, 2009: 357−359. SUN Kejun. Electrician Handbook[M]. Beijing:Chemical Industry Press, 2009: 357−359.

[15] 许肖梅. 声学基础[M]. 北京: 科学出版社, 2003: 47−49. XU Xiaomei.Acoustic Basis[M]. Beijing:Science Press, 2003: 47−49.

(编辑 高海燕)

Effect of phase-difference on grain refinement of the dual-source ultrasonic casting aluminum alloy

ZHANG Wu, LI Xiaoqian, PENG Hao, JIANG Ripeng

(College of Light Alloy, State Key Laboratory of High Performance Complex Manufacturing,Central South University, Changsha 410083, China)

The model of aluminum alloy dual-source ultrasonic casting bath was established, and the effects of different phase-differences on the bath sound field under the same and different frequencies were simulated with fluent software. The results of simulation show that under the same frequency, the distribution of sound field is significantly affected by phase-differences, and the cavitation domain decreases with increasing phase-difference; while phase-differences have no effect on the sound field distribution under difference frequencies. The dual-source casting conducted with different phase-differences under the same frequency shows little effects on the refinement of grains in the edge and ultrasound irradiation fields, and the refinement of grains in the center part deteriorates with increasing phase-difference. While under the condition of different frequencies, the phase-differences show no effect on the refinement of grains, and the refinement of grains in the center part is similar to that under the conditions of dual-source ultrasound with the same frequency and a phase-difference of 90°. Under the conditions of dual-source ultrasound with the same frequency and a phase-difference of 0°, the grain size decreases much compared to that conducted with dual-source ultrasound with different frequencies.

aluminum alloy; dual-source ultrasonic casting; phase difference; cavitation domain; grain refinement

TG249.7; TB559

A

1673−0224(2016)04−596−07

国家重点基础研究发展规划(973 计划) 资助项目：航空航天用高性能轻合金大型复杂结构件制造的基础研究(2010CB731706)；航空高性能轻合金材料的基础研究(2012CB619504)

2015−08−24；

2015−10−09

李晓谦，教授，博导，电话：0731-88877380；E-mail: meel@csu.edu.cn