混合实验法在W-Ni-Cu合金组分设计中的应用

辛思彧，郭从盛，董洪峰，景然



混合实验法在W-Ni-Cu合金组分设计中的应用

辛思彧，郭从盛，董洪峰，景然

(陕西理工大学材料科学与工程学院，汉中 723000)

采用极端顶点设计法设计W-Ni-Cu合金组分，将组分自变量与相对应的性能因变量(相对密度、显微硬度、抗弯强度)进行回归分析和规划求解，同时采用冷压烧结法制备不同组分的W-Ni-Cu合金，测定合金的密度、显微硬度和力学性能，研究组分对合金性能的影响。结果表明：回归方程复相关系数2=1，方程精确度高；合金性能随组分变化而呈规律变化；当Ni含量与Cu含量(均为质量分数)分别为3%和5%时，合金的综合力学性能最佳：相对密度为94.295%、显微硬度286.55、抗弯强度931.51 MPa。W-Ni-Cu合金的相对密度计算值与实验结果的误差为−0.45%～0.06%，显微硬度计算值与实验结果的误差为−8.48%～4.46%，抗弯强度计算值与实验结果的误差为−5.19%～4.15%。误差很小，说明混合实验和极端顶点设计法能优化W-Ni-Cu合金组分，并可靠预测合金性能。

极端顶点设计；W-Ni-Cu合金；组分设计；力学性能；冷压烧结

钨基高密度合金也被称作高密度合金或钨基重合金, 它是一种以钨为基体相, 加入少量Cu，Fe，Ni，Co，Mo，Cr等元素而构成的复合材料，广泛用于航天航空、军事及民用工业[1]。常见的三元系钨合金有：W-Ni-Fe，W-Ni-Cu，W-Ni-Co，W-Ni-Mn等。由Ni-W二元相图可看出，Ni可溶解约 45%(质量分数)的W，此时易形成脆性相，因此须添加其它合金化元素，以控制Ni/W元素相互作用。Cu具有优良的综合性能，可与Ni无限互溶，且熔点较低(Cu与Ni的熔点分别为1083 和1453 ℃)，可阻止脆性相的形成并降低烧结温度[2]。钨合金的成分配比对其组织和性能影响很大。李秋娟等[3]指出，当W-Ni-Cu合金中W的质量分数为93%时，合金性能最优，但没有研究不同粘结相元素的比例对合金性能的影响。马运柱等[4]从已有的文献报道中发现W-Ni-Fe合金中粘结相元素Ni与Fe的含量(质量分数)比控制在2~4之间时性能最优。王伏生等[5]采用加和密度计算法研究了W-Ni-Cu合金中粘结相组分对合金热膨胀系数的影响，但由于是以致密化程度为主要考虑因素，不能保证力学性能最优。因此需要寻找一种可以建立W-Ni-Cu合金组分与性能定量关系的方法，以实现合金的组分优化。混合实验法是一种通过建立组分自变量和性能因变量间的函数关系，实现组分优化的方法，已在切削机床主轴系统的优化、公差分配问题、药品配方优化和金刚石胎体配方等[6−11]领域得到有效应用。PARK等[10]用极端顶点设计法确定切削机床中主轴的尺寸为410 mm时在实际应用中得到优异的效果。方小红等[11]用混合实验法和极端顶点设计法对金刚石刀具进行铁基胎体配方的研究，得出在铁含量(质量分数)为48.5%时胎体硬度最高，与验证试验结果吻合。目前还没有混合实验法在W-Ni-Cu合金组分设计方面的应用。混合实验法是一种建立组分自变量和性能因变量间关系的方法；极端顶点设计法是一种数据处理方式，用以提供建立组分自变量和性能因变量间本构关系的数据。本研究采用混合实验法设计W-Ni-Cu合金组分，通过极端顶点设计、回归分析和优化求解，研究合金性能与元素含量间的关系，获得最优组分，并通过实验对研究结果的可靠性进行验证，以实现W-Ni-Cu合金的组分优化，强化合金性能。

1 确定变量

混合实验法中，个因素加和为1，即所有自变量(因素)x满足以下关系：

x为因素的百分比；a和b分别为x的取值下限与上限。考虑系统中个因素间的交互作用，使用次方程建立性能指标与成分指数x间的关系：

回归系数a，a，12…由最小二乘法求得。x，x，x…x分别为各组分的含量。对于本研究的W-Ni-Cu合金体系，x为各组分的含量，=3。令1，2，3分别为W，Ni，Cu元素的含量(质量分数)，根据实验经验及参考文献[12−14]选定1，2和3的取值范围分别为85%~93%，3%~12%和1%~5%。W-Ni-Cu合金性能为试验指标，包括相对密度、抗弯强度和显微硬度。

1.1 建立回归方程

根据上述1，2和3的取值范围和式(2)，得到回归方程的一般形式：

式中：1，2和3均为一次项，4~7为交互项，由于W，Ni，Cu三元素间相互作用很小，所以在本次试验所建立的方程中去掉7项[15]，得到如下回归方程：

1.2 建立因素空间的处理组合

在个因素中只有−1个因素的质量分数可在一定范围内变动，在个因素加和为1的约束条件下剩下的1个因素随之确定。选取i和b为2个顶点，符合要求的点所构成的子集称为极端顶点设计法。根据极端顶点设计法及取值范围得到因素空间的12个顶点，如表1所列。例如表1中的第1组数据，1取W含量范围的顶点0.85，2取Ni含量范围的顶点0.03，3即为1−0.85−0.03=0.12(Cu含量的取值)，因为0.12超出1%~5%的范围，所以表1中的第1组数据不可用。遵循此方法共得到6组有效数据，如表1所列。

表1 因素空间的处理组合

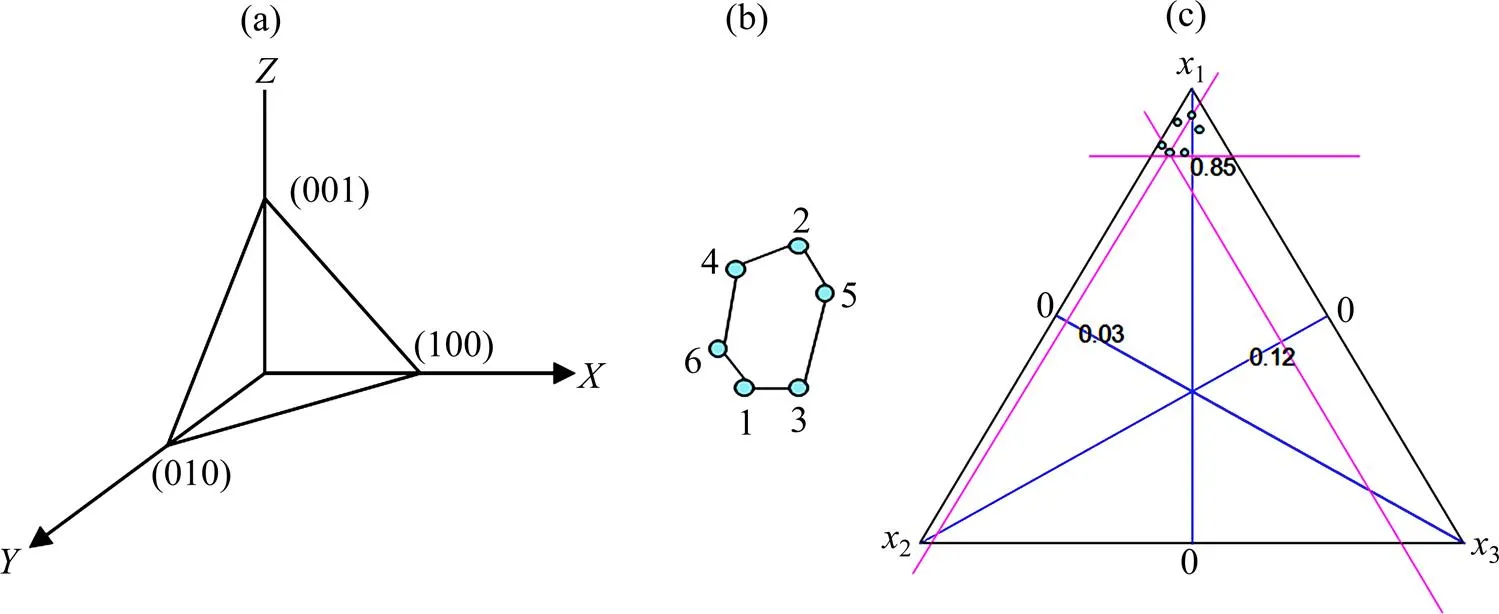
图1 响应曲面模型

1.3 立响应曲面模型

响应曲面模型是1个−1维的多面体，在本研究中=3，所以建立1个2面三角形来确定极端顶点，在(111)晶面上所有点加和为1，即++=1，因此极端顶点设计法在(111)晶面上取点，如图1(c)所示，得到的六边形为取值空间(图1(b))。

1.4 确定试验组分

六边形的边及六边形内部均为极端顶点设计法的可取值。在六边形的6个顶点中随机抽取5组数据作为表2中的1~5号合金组分，第6组数据为图1(b)所示六边形的形心，即取表1中6组有效值的平均数。

表2 W-Ni-Cu合金的名义成分

2 合金制备与性能检测

按表2中各组分的含量称取W粉、Ni粉和Cu粉，在三维涡流混料机(TD-2)中混料10 h，然后利用DY20电动粉末压片机在190 MPa压力下冷模压成形，脱模后的压坯放入SX3-6-16快速高温烧结炉中进行烧结，烧结温度 1400 ℃，保温60 min，升温速率3.39 ℃/min，随炉冷却至室温后取出，得到W-Ni-Cu合金，合金样品的尺寸列于表3。

表3 W-Ni-Cu合金样品的尺寸

采用排水法测量W-Ni-Cu合金的密度，并计算其相对密度。用FEM−7000图像显微硬度计测试合金的硬度。在CTM8020微机控制电子万能材料试验机上测试抗弯强度，每种组分的合金取3个样品进行检测，取平均值。合金性能列于表4。

3 实验数据处理

根据表4所列性能，使用Excel中的回归分析命令计算系数1~6，代入式(4)即分别得到W-Ni-Cu合金的相对密度、显微硬度和抗弯强度随组分变化的回归方程，再通过Excel中的规划求解命令计算最大相对密度、抗弯强度和显微硬度，研究约束条件下每种元素含量对W-Ni-Cu合金性能的影响。

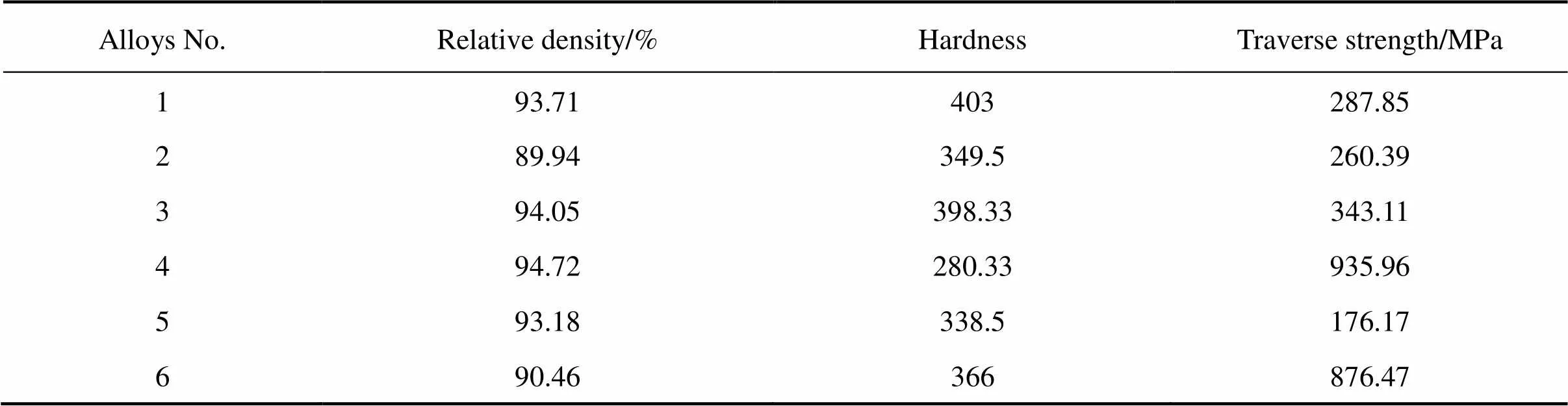
表4 表2中6组合金的性能测试结果

3.1 回归方程

由回归分析得到的W-Ni-Cu合金性能与组分间的回归方程如下：

1) 相对密度与组分关系的回归方程，2为复相关系数。

2=1

2) 显微硬度和组分关系的回归方程

2=1

3) 抗弯强度和组分关系的回归方程

2=1

式(5)，(6)和(7)中2代表自变量x与因变量的关联性，3个公式的2全部为1，说明W-Ni-Cu合金的相对密度、显微硬度和抗弯强度都与各组分的含量密切相关。因此混合实验和极端顶点设计法可用于预测有成分约束的W-Ni-Cu合金的相对密度、显微硬度和抗弯强度。

3.2 W，Ni，Cu元素含量对合金性能的影响

由于要画出各元素含量对各项性能的影响曲线，为了保证曲线精确，将各元素的含量在其取值范围内取20个点，(W)=85.2%，3%≤(Ni)≤12%，1%≤(Cu)≤5%。代入规划求解的Excel中求出对应答案，得到图2，3和4。

由图2，3和4可知各元素对显微硬度的影响规律与抗弯强度的影响规律刚好相反。各元素的最佳取值范围列于表5。在最优范围基础上，以抗弯强度性能为主，显微硬度和相对密度为辅的条件下，经分析得到的最优组分为92W-3Ni-5Cu合金。

图2 钨、镍、铜元素含量对W-Ni-Cu合金相对密度的影响

图3 钨、镍、铜元素含量对W-Ni-Cu合金显微硬度的影响

4 实验结果与计算结果对比

表6，7和8所列为6组不同成分合金性能的实验结果和预测结果的对比，根据二者的误差来分析回归方程的精确性。由表可见相对密度的误差不超过1.94%，显微硬度的误差不超过8.66%，抗弯强度的误差不超过5.19%。预测值与测试值相差很小，这表明混合实验和极端顶点设计对于W-Ni-Cu合金性能的预测结果是可靠的。

图4 钨、镍、铜元素含量对W-Ni-Cu合金对抗弯强度的影响

表5 合金最佳性能对应的元素含量

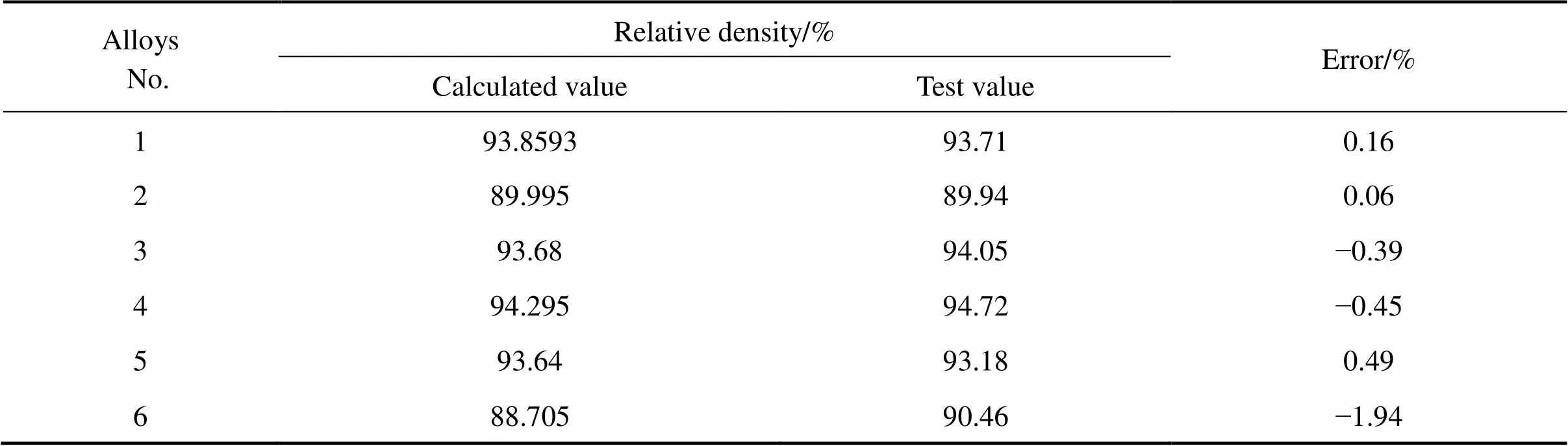
表6 相对密度预测结果和实验结果的对比

表7 显微硬度测试值和实验值比较

表8 抗弯强度测试值和实验值比较

5 结论

1) 混合实验极端顶点设计法能可靠地预测高密度W-Ni-Cu合金的各项性能，以及合金组分对性能的影响。

2) 采用Excel中的回归和规划求解命令可快速有效地解决混合实验极端顶点设计实验中的优化问题。

3) 预测结果表明，W-Ni-Cu合金的最优组分为92W-3Ni-5Cu，该合金的综合性能最优。相对密度、显微硬度和抗弯强度的实验结果分别为94.72%，280.33和935.96 MPa；预测结果分别为94.295%，286.55和931.51 MPa，这3项性能的实验结果与预测结果的误差分别为−0.45%，2.22%和−0.48% 。预测结果可靠。

[1] 王松, 谢明. 高密度钨合金的研究现状与发展趋势[J]. 稀有金属材料与工程, 2012, 41(S2): 145−148. WANG Song, XIE Ming. Present research and future development of tungsten heavy alloys[J]. Rare Metal Materlalsand Engineering. 2012, 41(S2): 145−148.

[2] 马国刚. W基重合金的成分设计和性能[J]. 五邑大学学报: 自然科学版, 2007, 20(4): 38−41. MA Guogang. The composition design and performance of W heavy alloys[J]. Journal of WUYI University (Natural Science Edition), 2007, 20(4): 38−41.

[3] 李秋娟, 赵慕岳. W-Ni-Cu-Sn 系高比重合金的研究 [J]. 粉末冶金技术, 1988, 6(4): 200−200. LI Qiujuan, ZHAO Muyue. Investigation on W-Ni-Cu-Sn heavy alloys[J]. Powder Metallurgy Technology, 1988, 6(4): 200−200.

[4] 马运柱, 黄伯云, 刘文胜. 钨基合金材料的研究现状及其发展趋势[J]. 粉末冶金工业, 2005, 15(5): 46−53. MA Yunzhu, HUANG Boyun, LIU Wen-sheng. Status and development of tungsten-based alloy research[J]. Powder Metallurgy Industry, 2005, 15(5): 46−53.

[5] 王伏生, 梁容海, 金展鹏. W-Ni-Cu合金中粘结相对膨胀系数等性能的影响[J]. 粉末冶金材料科学与工程, 1997, 2(3): 229−233. WANG Fusheng, LIANG Ronghai, JIN Zhanpeng.A study of the relation between binding phase and expan sion coefficient in W-Ni-Cu alloys[J]. Powder Metallurgy Materials Science and Engineering, 1997, 2(3): 229−233.

[6] ŞEHIRLIOĞLU A K, ÖZLER C. The use of mixture experiments in tolerance allocation problems[J]. The International Journal of Advanced Manufacturing Technology, 2008, 35(7/8): 769−777.

[7] 王丹薇, 杜红, 朱庆文, 等. 混合实验法优化含胆固醇微乳处方[J]. 北京中医药, 2013, 32(4): 304−307. WANG Danwei, DU Hong, ZHU Qingwen, et al. Mixed experiment method for optimization of cholesterol-involved microemulsion prescription[J]. Beijing Journal of Traditional Chinese Medicine, April, 2013, 32(4): 304−307.

[8] 董洪峰. 新型金属基金刚石复合材料工磨具的试制和性能研究[D]. 兰州: 兰州理工大学, 2013: 17−27. DONG Hongfeng. The preparation and property research on new P/M metal based diamond composite sawing and grinding[D]. Lanzhou: Lanzhou University of Technology, 2013: 17−27.

[9] 高中滨. 混料均匀试验设计方法研究[D]. 广州: 华南理工大学, 2011: 12−17. GAO Zhongbin. Study of uniform design for mixture experiments[D]. Guangzhou: South China University of Technology, 2011, 12−17.

[10] PARK S, LEE C, HWANG Y. Lightweight design of 45000 r/min spindle using full factorial design and extreme vertices design methods[J]. Journal of Central South University of Technology, 2011, 18(1): 153−158.

[11] 方小红, 潘秉锁, 杨凯华. 极端顶点设计在热压金刚石工具胎体配方试验中的应用[J]. 金刚石与磨料磨具工程, 2008(2): 33−36. FANG Xiaohong, PAN Bingsuo, YANG Kaihua. Application of extreme vertices design in matrix formula experiment for hot pressing diamond tools[J]. Diamond Abrasives Engineering, 2008(2): 33−36.

[12] 黄劲松, 周继承, 黄伯云. 元素及其化合物对钨基高密度合金性能的影响[J]. 稀有金属材料与工程, 2004, 33(5): 454−458. HUANG Jinsong, ZHOU Jicheng, HUANG Boyun. Effects of elements and their compounds on properties of high density alloy[J]. Rare Metal Materlals and Engineering, 2004, 33(5): 454−458.

[13] DAS J, RAO G A, PABI S K. Microstructure and mechanical properties of tungsten heavy alloys[J]. Materials Science and Engineering: A, 2010, 527(29/30): 7841−7847.

[14] SHEN J, CAMPBELL L, SURI P, et al. Quantitative microstructure analysis of tungsten heavy alloys (W-Ni-Cu) during initial stage liquid phase sintering[J]. International Journal of Refractory Metals and Hard Materials, 2005, 23(2): 99−108.

[15] 张启运, 庄鸿寿. 三元合金相图手册[M]. 北京: 机械工业出版社, 2011: 386. ZHANG Qiyun, ZHUANG Hongshou. Ternary Alloy Phase Diagrams[M]. Beijing: China Machine Press, 2011: 386.

(编辑 汤金芝)

Application of mixture experiments in the composition design of W-Ni-Cu alloys

XIN Siyu, GUO Congsheng, DONG Hongfeng, JING Ran

(College of Materials Science and Engineering, Shanxi University of Technology, Hanzhong 723000, China)

The compositions of W-Ni-Cu alloys were designed via the extreme vertex design method. The composition as independent variable and their corresponding properties as dependent variable (such as relative density, micro-hardness, bending strength) were analyzed by using regression and the programming solver. The W-Ni-Cu alloys were prepared by cool isostatic pressing and sintering, and the effect of the composition on the properties of alloys was studied by testing the density, micro-hardness and mechanical properties. The results show that the multiple correlation coefficient2of the regression equation is about 1, and the properties of the alloys change regularly with the variation of compositions. When the mass fractions of Ni and Cu are 3% and 5%, respectively, the optimal mechanical properties with the relative density of 94.295%, the micro-hardness of 286.55 and the bend strength of 931.51 MPa are obtained. The relative density error value of the W-Ni-Cu alloys between calculated value and experimental value is about −0.45%−0.06%, and the micro-hardness error value and the bending strength error value are −8.48%−4.46% and 5.19%−4.15%, respectively. Therefore, the extreme vertex design method can be used to optimize the composition of W-Ni-Cu alloys, and predict the properties of the alloys.

extreme vertex design; W-Ni-Cu alloys; composition design; mechanical property; cool isostatic pressing

TB31

A

1673−0224(2016)04−527−07

陕西理工大学校级人才启动项目(SLGQD13(2)-17)；陕西省教育厅专项科研计划项目(14JK1146)

2015−08−24；

2015−12−21

郭从盛，教授。电话：13060463297；E-mail: 530981733@qq.com