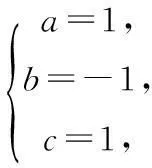高一数学测试
2016-03-04
高一数学测试
一、填空题(本大题共14小题,每小题5分,共70分)
1.若集合M=(-1,1),N=[0,2],则集合M∪N=______.
2.下面各组函数中为相同函数的序号是______(填序号).



④f(x)=log2(x+1)+log2(x-1),
g(x)=log2(x2-1).
3.已知log7[log3(log2x)]=0,则x-1=______.
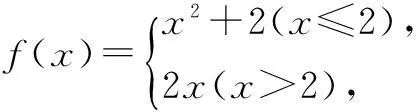
5.设集合M={x|0≤log2x<1},N={x|x≤a},若M∩N≠∅,则a的取值范围是______.
6.若函数y=2x-(b-1)图象不经过第二象限,则b的范围是______.
7.设f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x+b(b为常数),则f(-1)=______.
9.已知a=log0.20.4,b=log0.20.3,c=log0.43,d=log0.30.2,则a,b,c,d的大小关系是______.
10.幂函数y=xm2-2m-3(m∈Z,x≠0)的图象与x,y轴都无交点,且关于y轴对称,则m为______.
11.关于x的方程|x2-1|=a有三个不等的实数解,则实数a的值是______.
12.函数f(x)是R上的奇函数,且在(0,+∞)内是增函数,又f(-3)=0,则(x-2)f(x)<0的解集为______.
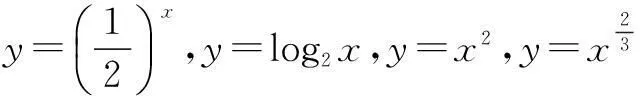
14.下列说法中:① 若f(x)=ax2+(2a+b)x+2 (其中x∈[2a-1,a+4])是偶函数,则实数b=2;②f(x)表示-2x+2与-2x2+4x+2中的较小者,则函数f(x)的最大值为1;③ 若函数f(x)=|2x+a|的单调递增区间是[3,+∞]),则a=-6;④ 已知f(x)是定义在R上的不恒为零的函数,且对任意的x,y∈R都满足f(x·y)=x·f(y)+y·f(x),则f(x)是奇函数.其中正确说法的序号是______(注:把你认为是正确的序号都填上).
二、解答题(本大题共6小题,共90分,解答应写出必要的文字说明、证明过程或演算步骤)

(1)求a的值及A,B;
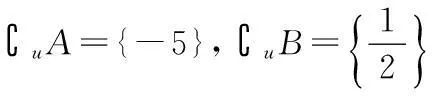
(2)设全集U=A∪B,求(uA)∪(uB).
(1)若a=1,求集合A;
(2)若A∩B=A,求实数a的值.
17.(本小题满分15分)某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元,销售单价与日均销售量的关系如下表所示:

销售单价/元6789101112日均销售量/桶480440400360320280240
请根据以上数据作出分析, 这个经营部怎样定价才能获得最大利润?
18.(本小题满分15分)已知二次函数f(x)满足f(x+1)-f(x)=2x,且f(0)=1.
(1)求f(x)的解析式;
(2)若函数y=f(x+m)在[-1,1]上单调,求m的取值范围;
(3)当x∈[-1,1]时,不等式f(x)>2x+m恒成立,求实数m的范围.

x…0.511.51.71.922.12.22.33457…y…1475.335.115.0155.015.045.085.6778.612.14…
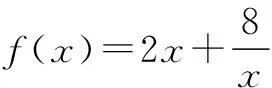
20.(本小题满分16分)如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx(m>c>1)的图象交于点C,且AC与x轴平行.
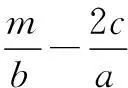
(3)已知h(x)=ax,φ(x)=bx,若x1,x2为区间(a,b)内任意两个变量,且x1 求证:h(f(x2))<φ(f(x1)). 参考答案 一、填空题 5.a<1;6.b≥2;7.-3;8.[0,2]; 9.c 12.(-3,0)∪(2,3);13.2;14.① ③ ④. 二、解答题 15.(1) 由2∈A得8+2a+2=0, 解得a=-5. 16.(1)(2-x)(x-3a-1)>0,当a=1时,(2-x)(x-4)>0,集合A={x|2 (2)由题意,可知B=[2,+∞), 由A∩B=A得A⊆B. ② 若2=3a+1时,不合题意; 17.根据上表,销售单价每增加1元,日均销售量就减少40桶. 设在进价基础上增加x元后,日均销售利润为y元,而在此情况下的日均销售量为 480-40(x-1)=520-40x. 由于x>0,且520-40x>0,即0 于是可得 y=(520-40x)x-200=-40x2+520x-200, 其中0 所以,只需将销售单价定为11.5元, 就可获得最大的利润. 18.(1)令f(x)=ax2+bx+c(a≠0),代入 得a(x+1)2+b(x+1)+c-(ax2+bx+c)=2x,2ax+a+b=2x恒成立, (2)y=f(x+m)=(x+m)2-(x+m)+1 =x2+(2m-1)x+1-m, (3)当x∈[-1,1]时,f(x)>2x+m恒成立,即x2-3x+1>m恒成立. 令g(x)=x2-3x+1 g(x)min=g(1)=-1, ∴m<-1. 19.(1)由表中可知f(x)在(0,2]为减函数,[2,+∞)为增函数,并且当x=2时,f(x)min=5. (2)证明:设0 又0 所以f(x1)-f(x2)>0,即f(x1)>f(x2),所以f(x)在(0,2]为减函数. f(x)min=f(2)=5. 20.(1)由题意,得A(2,log32),B(4,log34),C(4,logm4),又AC与x轴平行,所以logm4=log32,所以m=9. (2)由题意,得A(a,logca),B(b,logcb),C(b,logmb) 因为AC与x轴平行,所以logmb=logca. 因为b=a2,所以m=c2,所以 (3)证明:因为a logca 又因为a>1,b>1,所以 alogcx2 又因为logcblogca=logcalogcb,所以 logcalogcb=logcblogca. 所以alogcb=blogca,alogcx2 即h[f(x2)]<φ[f(x1)]). ○课外测试○