真的是“循环论证”吗——对一道试题数学归纳法解法的探究



真的是“循环论证”吗
——对一道试题数学归纳法解法的探究

潘神龙

(广东省广州市番禺区实验中学 ，511400)

数学归纳法是一种特殊的证明方法,主要用于研究与正整数有关的数学问题,体现了人的认识从有限到无限的飞跃,在数学的发展中起着重要的作用．

2014年广东高考(理)数列解答题考查学生的推理意识,避免一味的机械应试训练,着重考查了数学归纳法．受前几年题目的影响,不少教师在已知递推公式求通项公式上训练了不少,却对数学归纳法缺乏研究,出现一些教学瓶颈．

2015年广州市一模数列解答题(题目见下),可用数学归纳法进行求解,有教师认为这是“循环论证”.对此，本文谈点笔者的认识,以期与同行探讨,共同提高．

一、问题由来

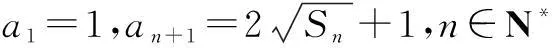
解猜想an=2n-1.下面用数学归纳法证明.

①n=1时，命题成立.

由① ②,对任意∀n∈N*,an=2n-1.

有教师认为,这是“循环论证”:假设n=k时命题成立,不能说明n

二、追本溯源

正所谓,给学生一杯水,教师就要有长流水．

1.数学归纳法

数学归纳法起源于最小数原理(正整数集的任意非空子集必有一个最小数),是有意地以形式相同、范围较小的命题成立性为前提,来不断推导更大范围内命题的成立性,体现了递推的思想．教材上出现的是第一数学归纳法,其实还有第二数学归纳法,步骤如下: (1)证明n=n0时,命题成立； (2)假设n≤k(n≥n0)时,命题成立，证明n=k+1时,命题也成立．由(1) (2),对所有正整数n(n≥n0),命题都成立．

证明假设命题不是对所有正整数n(n≥n0)都成立.令M表示使命题不成立的正整数所成的集合,M≠∅．由最小数原理,M中有最小数m,m>n0,且命题对m不成立，所以m-1是正整数,且命题对所有的n(n0≤n≤m-1)都成立；由(2)知,命题对m也成立,矛盾,证毕．

数学理论已经证明了第一数学归纳法与第二数学归纳法是等价的．

2.“循环论证”

“循环论证”是指在证明的过程中,把命题的结论作为证明的论据使用,又称为“先定结论”．第一数学归纳法中的“循环论证”是指从“假设n=k时命题成立”到“证明n=k+1时命题也成立”时,启用了不完全归纳的结论．

三、拨云见日

另外,有教师认为,将② 中“n=k”改为“n≤k”即可,这实质上是使用第二数学归纳法．由两种数学归纳法的等价性可知,当“n≤k”是正确时,“n=k”也是正确的．而且,本解法考查的是推理意识,学生也没有接触过第二数学归纳法,若纠缠于“n=k”还是“n≤k”,未免有些舍本逐末．

四、他石攻玉

解猜想an=2n+1,下面用数学归纳法证明.

① 当n=1，易知命题成立.

② 假设n=k(k≥1)时，ak=2k+1,则Sk=3+5+7+…+(2k+1)=k(k+2)；再结合条件Sk=2kak+1-3k2-4k,解得ak+1=2(k+1)+1,命题成立.

由① ②,对任意n∈N*，an=2n+1.

本解法和上述广一模的解法是一致的.多家网站(包括学科网)均收录了这个解法，可见,“循环论证”的疑惑是没有必要的．

由第(1)问，得

ex-1-x≥0,

即ex-1≥x，

当且仅当x=0时取等号.