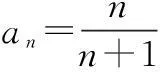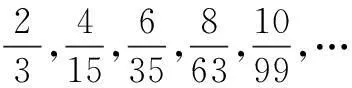数列的概念与简单表示(第一课时)教学设计

2016-03-04邓春生

高中数学教与学 2016年2期

关键词：通项实例意图

邓春生

(江苏省海门市麒麟中学，226125)

教学目标

(1)知识与技能:理解数列的概念及其表示方法,了解数列和函数之间的关系;理解数列的通项公式,并会用通项公式写出数列的任意一项;对于比较简单的数列,会根据给定的前几项写出它的一个通项公式．

(2)过程与方法:通过对一列数的观察、归纳,写出符合条件的一个通项公式,培养学生的观察能力和抽象概括能力．

(3)情感态度与价值观:通过本节课的学习,让学生体会数学来源于生活,提高学生数学学习的兴趣．同时通过对数学问题的观察、探究和归纳,培养学生的探索和进取精神．

教学重点

理解数列的概念,能从函数的观点认识数列,理解数列的通项公式及应用．

教学难点

数列与函数的关系的理解;根据数列的前几项抽象、归纳出数列的通项公式．

教学过程

一、创设问题情境(7个实例)

(1) 观察钢管堆放示意图(如图1),自上而下各层钢管根数依次是:4,5,6,7,8,9,10.

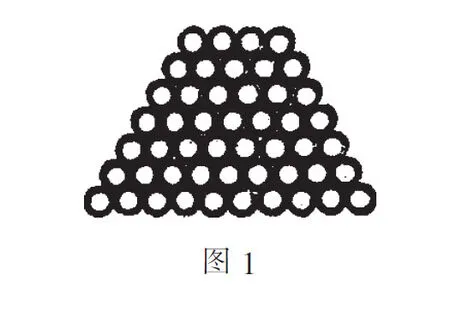
(2) 观察钢管堆放示意图,自下而上各层钢管根数依次是:10,9,8,7,6,5,4.

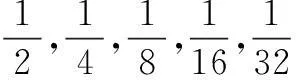
(4) 请大家拿出一张纸,假设它的厚度是1,我们现在把它对折,这时纸张的厚度是多少?再把它对折,这时纸张的厚度又是多少?再对折,厚度呢?依此类推,每次对折后纸张的厚度依次构成一列数:2,4,8,16,32,…

(5)-1的1次幂、2次幂、3次幂、…排列成一列数:-1,1,-1,1,-1,…

(6) 无穷多个1排列成的一列数:1,1,1,1,1,…

(7)从1984年至今,我国体育健儿共参加了八届奥运会,获得的金牌数依次排成一列数:15,5,16,16,28,32,51,38.

设计意图创设情境,激发兴趣,引入新课．用多媒体展示学生熟知的7个实例,增强了感性认识,调动学生学习新知识的积极性．

问题1请同学们观察这些具体的例子,看它们有何共同特点?

设计意图提出问题,思考归纳,形成概念．学生可进行自我表述、小组讨论、教师点拨,逐步归纳,形成共识——这些具体例子的共同特点:它们均是一列数，都有一定次序. 学生尝试归纳数列的定义,培养学生的抽象概括能力．

二、讲授新课

1. 数列的定义

按照一定次序排列的一列数叫做数列.(教师板书)

问题2请同学们结合数列的定义和上述具体实例,说说数列中的每一个数和集合中的元素有什么区别?

设计意图实例辨别,加深概念理解．继续利用多媒体展示7个实例，使学生把数列中的数和集合中的元素区分开来:

(1)数列中的数一定是“数”,而集合中的元素不一定是“数”．

(2)数列中的数是按一定次序排列的,因此,如果组成两个数列的数相同而排列次序不同,那么它们就是不同的数列(如实例(1)(2));而集合中的元素是无序的．

(3)数列定义中并没有规定数列中的数必须不同,因此,同一个数在数列中可以重复出现;而集合中的元素不能重复出现(如实例(5)(6))．

2. 数列的项

数列中的每个数都叫做这个数列的项. 各项依次叫做这个数列的第1项(或首项),第2项,…,第n 项,….

3. 数列的一般形式

a1,a2,a3,…,an,…,简记为{an},其中an是数列的第n项．

问题3 下面我们再来看这些数列的每一项与这一项的序号是否有一定的对应关系?这一关系可否用一个公式表示?

以实例(1)为例(其余实例略):

第1层钢管数为4;即:1↔4=1+3

第2层钢管数为5;即:2↔5=2+3

第3层钢管数为6;即:3↔6=3+3

第4层钢管数为7;即:4↔7=4+3

第5层钢管数为8;即:5↔8=5+3

第6层钢管数为9;即:6↔9=6+3

第7层钢管数为10;即:7↔10=7+3

若用an表示钢管数,n表示层数,则可得出每一层的钢管数可用一个公式an=n+3,(1≤n≤7,n∈N*)来表示其对应关系．

设计意图本节课的重点是数列的概念及通项公式,因为数列的概念是学生学习本章知识的基础,数列的通项公式又是研究后面等差数列、等比数列的灵魂．在此教师务必要放慢速度,花足时间,向学生讲清讲透,不能一带而过．

4. 数列的通项公式

如果数列{an}的第n项an与n之间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的通项公式．

问题4试一试:你能写出前面问题情境中其余数列的通项公式吗?

设计意图对刚才所讲的概念进行及时巩固与消化．教师巡视指导,尤其是实例(5),每个学生不可能将几种情况都写出来,教师可以根据不同学生书写的情况进行展示、点评、总结与补充．对于一组数列的通项公式,问题的解答常常不是唯一的．只要能得出一个使所给的各项都能满足的,最简捷的公式就可以了．下面是实例(2)、(3)、(5)、(6)的通项公式：

(2)an=11-n(1≤n≤7,n∈N*).

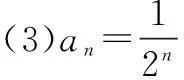
(5)an=(-1)n，或an=cosnπ，

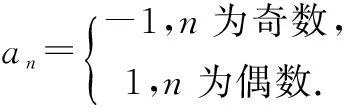
(6)an=1.

问题5通过上述实例的研究,你对数列通项公式有什么样的认识?你又是如何理解数列的通项公式的?

设计意图让学生在此对数列的通项公式有一个比较深刻的全面的认识．结合对应关系,回顾函数概念,揭示数列与函数的关系．这是一个难点,讲解必须清楚、透彻．树立从函数观点看待数列问题的意识．

(1)并不是所有数列都能写出(或方便写出)其通项公式,如实例(7)．

(2)一个数列的通项公式的形式有时是不唯一的,如实例(5)．

(3)数列的通项公式具有双重身份,它表示了数列的第n项,又是这个数列中所有各项的一般表示．它反映了一个数列项与项数的一种对应关系(函数关系)．

5. 数列与函数的关系

数列可以看成以正整数集N*(或它的有限子集{1,2,3,…,n})为定义域的函数an=f(n),当自变量从小到大依次取值时可得到对应的一列函数值．反过来,对于函数y=f(x),如果f(i)(i=1,2,3,…,n,…)有意义,那么我们可以得到一个数列f(1),f(2),f(3),f(4),…,f(n),…

因此，数列可以看作特殊的函数,项数是其自变量,其定义域是正整数集或正整数集的有限子集，其解析式就是数列的通项公式．

6.数列的表示

通项公式法、列表法、图象法．(结合实例总结)

7.数列的分类

(1)根据数列项数的多少划分:

有穷数列:项数有限的数列.如实例(1)(2)(7)是有穷数列．

无穷数列:项数无限的数列.如实例(3)(4)(5)(6) 是无穷数列．

(2)根据数列项的大小划分:

递增数列:从第2项起,每一项都大于它的前一项的数列,即an>an-1,(n≥2)．如实例(1)(4)．

递减数列:从第2项起,每一项都小于它的前一项的数列,即an-1

常数数列:各项相等的数列,即an+1=an或an=c,(n∈N*,c为常数)．如实例(6)．

摆动数列:从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列．如实例(5)(7)．