不等高支承对双塔单跨悬索桥主缆的影响分析*
2016-03-04贺耀北段瑞芳王晓明
贺耀北 段瑞芳 王晓明
(湖南省交通规划勘察设计院1) 长沙 410008)
(陕西交通职业技术学院2) 西安 710018) (长安大学桥梁工程研究所3) 西安 710064)
不等高支承对双塔单跨悬索桥主缆的影响分析*
贺耀北1)段瑞芳2)王晓明3)
(湖南省交通规划勘察设计院1)长沙410008)
(陕西交通职业技术学院2)西安710018)(长安大学桥梁工程研究所3)西安710064)
摘要:为了分析主缆不等高支承对其受力和线形的影响,针对主缆不等高支承这一特殊形式的双塔悬索桥,建立有限元计算模型,对主缆的受力和线形进行分析.选择相应的几个主缆关键参数,提取各参数的变化数据,结合相应解析计算公式和辅助细部修正,对数据进行分析和曲线拟合,得到不等高支承对主缆的影响程度和趋势.结果表明,不等高支承对主缆的受力和线形会有较大的影响,会导致主缆的内力和主塔的竖向支反力增大,总体线形偏移,且高塔侧主缆尤为产生较大的影响.
关键词:桥梁工程;悬索桥;主缆;不等高支承;有限元法
贺耀北(1983- ):男,硕士,工程师,主要研究领域为大跨度桥梁设计
*国家自然科学青年基金项目(批准号:51308055)、教育部高校博士新教师基金项目(批准号:20130205120001)、中国博士后科学基金项目(批准号:2013M532000)、中央高校基本科研业务费项目(批准号:CHD2013G1211010)资助
0引言
悬索桥是当今大跨度桥梁中的一种重要形式,当前我国公路不断向高山深谷延伸,复杂的地形也决定了不等高桥塔今后将越来越多的出现,这一特殊形式桥梁也拥有着极大的研究价值.
悬索桥的主缆对整桥的受力和线形起到决定性作用,国内有许多文献对悬索桥主缆在成桥阶段和施工阶段的计算都有着较多的研究[1-3],且大部分都是单纯的理论解析计算法,也有文献采用有限元法和解析法相结合[4-5].对于非对称悬索桥,研究还是比较少也,只是针对主缆最大轴力、索鞍预偏量等进行了分析[6],并未对主缆的关键性因素进行变化趋势分析.
文中首先确定了主缆线形和受力的计算方法与其关键参数的选取以及相关修正.然后确立计算方案,进行需要的参数识别并建立有限元计算模型.(1)针对主缆受力影响方面,分析不等高支承对于主缆各个关键位置的内力、各支点竖向压力的影响趋势以及程度.(2)建模分析并进行修正计算和数据提取.对于主缆线形的关键点:总体线形、索鞍处切线角、主缆无应力长度及伸长量等进行分析,并与受力分析结果相结合,得出相应的研究结论.
1不等高支承对主缆影响分析方法
1.1基本假定
文中视主缆为理想悬链线,采用悬链线力学公式进行解析计算,主要有以下3个基本假定:(1)主缆视为理想柔性,不受弯也不受压;(2)主缆材料符合虎克定律,本构成线性变化;(3)忽略主缆截面面积和自重集度在外力作用下的变化.
1.2主缆不等高支承的作用分析
对于索结构而言,支点不对称将会引起线形的偏移和内力重分布.当2支点高度相同时,主缆中点为线形最低点,此时主缆内力最小;当一侧支点高度抬高h时,其线形的最低点向另一侧偏移a,索力也发生重分布,见图1.

图1 悬链线在不等高支点中示意图
主缆内力重分布后,由桥塔处受力分析可知,中跨主缆内力的变化和对应两入鞍切线角的变化必然引起该侧水平力发生变化,为平衡产生的不平衡力,则边跨侧的桥塔入鞍切线角也将发生变化,同理,继续以边跨结果推算出锚跨,以锚跨的初始条件完成锚跨的相应计算.
1.3参数的选取
采用有限元软件建模分析及悬索桥解析计算法结合的计算方式,针对该桥梁的2桥塔不等高支承的形式进行分析,采用适当的不等高数值选择多方案,进行计算分析对比,选择能够反映悬索桥主缆整体受力及线形的数据:主缆各关键位置的内力、各支点竖向压力、主缆总体线形、索鞍处切线角、主缆无应力长度及伸长量等.通过对数值计算结果进行曲线拟合、数据分析,综合研究其受塔顶不等高支承的影响作用及其程度和变化特点.为扩大适用范围,将塔顶标高高差计算范围取为0~20 m(右侧桥塔高于左侧),每隔1 m取一组计算数据,共21组.关注的主缆内力计算内容有:主索鞍处主缆内力、边索鞍处主缆内力、主缆对各支点竖向压力.对主缆内力的取点位置见图2,主缆对各支点竖向压力位置见图3.

图2 主缆内力取位示意图

图3 主缆对各支点压力取位示意图
1.4数据修正
主缆在索鞍处的实际线形为入鞍时首先切于圆弧面,而后由另一个切点离开索鞍,此过程不存在相对位移[7-8].显然和图4的理论计算线形不一致,对计算无应力长度的高精度要求需进行鞍部细部索长修正[9-10].
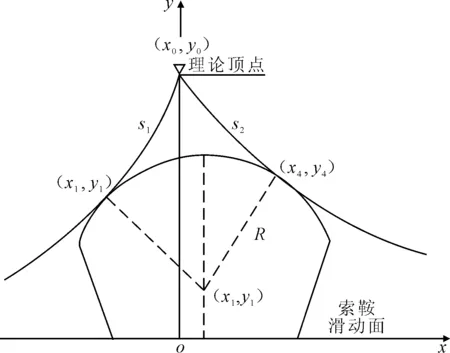
图4 主索鞍细部理论示意图
图中S1和S2修正的修正量分别为
式中:E为主缆弹性模量,MPa;H1,V1为索鞍处左跨主缆水平和竖向分力,kN;H2,V2为索鞍处右跨主缆水平和竖向分力,kN;A1,A2为索鞍处左右跨的主缆截面面积,m2;W1,W2为索鞍处左右跨的主缆荷载,kN/m;dS1,dS2为索鞍处左右跨主缆的修正量.
2工程背景
依托一复杂山区地形下的正在修建的两塔地锚式悬索桥,该桥的主桥设计为单跨简支悬索桥,主跨跨径为628 m,桥梁的整体布置为166 m+628 m+166 m,桥梁中跨的矢跨比设计为1∶10.由于地形限制,该悬索桥设计为两侧不等高桥塔,两桥塔顶标高高差差达10.362 m,成为典型的两桥塔塔顶不等高支承悬索桥.依托工程的全桥示意图见图5,右侧桥塔索鞍IP点比左侧高10.362 m.由于文章主要针对主缆变形和内力进行计算分析,故只需建立一仅有主缆的模型来研究,见图6,主缆特性见表1,选用索单元建模求解.

图5 依托工程示意图

图6主缆计算模型示意图

表1 主缆几何及材料参数
3不等高支承对主缆受力的影响
3.1不等高支承对主索鞍处主缆内力的影响分析
依据前述方案及提取的数据进行结果计算分析,两桥塔主索鞍两侧主缆内力和水平拉力随桥塔高差的拟合曲线见图7.

图7 主索鞍两侧主缆张力和水平拉力随桥塔高差的变化图
由图7可见,主缆内力的变化随2桥塔的高差线性变化,2桥塔高差对左主索鞍左侧和右主索鞍右侧两处的内力影响很小,主要是因为在全桥荷载没有变化的前提下,2桥塔的高差只是改变了几何线形,对缆力影响有限.而对于左主索鞍右侧和右主索鞍左侧这两处的内力,随桥塔高差的变化有明显变化,当桥塔高差增加20 m时,左主索鞍右侧的缆力减小了730 kN,右主索鞍左侧的缆力增加了1119.1 kN,变化幅值在1%~1.5%,说明桥塔高差的变化对跨中缆力有较显著的负面影响.
为明显表示,选取5种高差0,5,10,15,20 m进行中跨各吊点主缆内力分析,以左主鞍IP点为原点,内力取各分点顺桥向左侧力,见图8.
由图8可见,在不同桥塔高差取值的情况下,中跨顺桥向缆力变化幅值较接近,走势有整体偏移的情况.没有高差时,即主缆等高支承时,缆力分布合理,呈悬链线形,内力差距最小,最低点下探较深.随高差的增大,曲线整体左移,同时最低点上移,受力有整体增大的趋势.随高差增大,主缆内力从跨中向右侧(较高侧)主索鞍处增大变快,使得右主索鞍左侧缆力的增大量大于左主索鞍右侧缆力的减小量.
这一受力情况说明,对不等高桥塔悬索桥的中跨,靠近高塔侧的受力情形随塔高的增加更为不利,且呈现出距跨中越远、越靠近高侧主索鞍的区域越不利的趋势.
3.2不等高支承对散索鞍处主缆内力的影响分析
对两散索鞍处内力随桥塔高差变化取值拟合成曲线并分析同时取高差0,5,10,15,20 m对边跨主缆内力分析.见图9~12.

图9 左右散索鞍不同位置缆力随高差变化图

图10 不同桥塔高差对左边跨各分点内力变化图

图11 不同桥塔高差对右边跨各分点内力变化图
由图9、图10可知,随高差的增大,散索鞍各处缆力发生近似线形的变化,且幅值不大,约为166 kN的内力.可见在全桥荷载未增加的情况下散索鞍各处主缆内力增加幅值有限.且散索鞍未发生较大位移,因此对边跨内力影响较小.由于散索鞍位移小,使得边跨线形变化不明显,对边跨主缆内力影响较小,且随桥塔的升高内力也稳定升高,因此对边跨主缆受力基本没影响.

图12 散索鞍不同位置水平张力随高差变化图
而对于散索鞍处的水平张力由于绝对值差距较大,使得图12增加趋势并不明显.从右散索鞍左侧及左散索鞍右侧主缆水平力稍大于左散索鞍左侧及右散索鞍右侧的现象可看出,主缆内力变化经散索鞍区域后发生折减.结合之前对中跨的分析,也可反映出不等高支承对全桥受力的影响从桥塔IP点向整桥两端在削弱.
3.3不等高支承对锚面处主缆内力的影响分析
桥塔高差变化对锚面中心等效主缆的变化见图13.随着两桥塔高差取值由0 m增大到20 m,左锚面中心等效主缆内力增大了167.4 kN,右锚面中心等效主缆内力增大了166.6 kN.由之前分析可知,这与左散索鞍左侧和右散索鞍右侧主缆张力变化量完全相等.由此可见两桥塔的高差变化对锚跨受力几乎没有影响,锚跨主缆内力的变化只是由边跨传递而来,是边跨缆力变化值的累加.
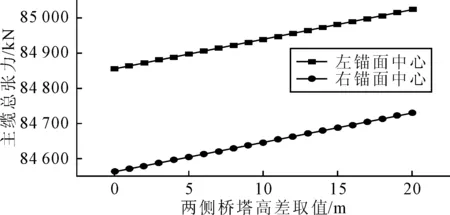
图13 桥塔高差变化对锚面中心等效主缆的变化
3.4不等高支承对主缆各支点竖向压力影响分析
主缆对各支点的竖向压力包括:非鞍槽中主缆对支点竖向压力(包括左右两侧缆力的竖向分力)和鞍槽内主缆自重.非鞍槽内主缆对支点的竖向压力可由之前总缆力的出鞍角的三角关系算出;鞍槽内主缆重量需依据图纸,按各段弧线及对应的半径和度数算出鞍槽内主缆的长度,再进行圆弧修正,得到鞍槽内主缆长度.根据文章的假定3,用该长度和每延米重度可算出槽内的主缆自重.见图14~16.

图14 主缆对主索鞍竖向压力随桥塔高变化曲线

图15 主缆对散索鞍竖向压力随桥塔高差变化曲线

图16 主缆对锚面处竖向压力随桥塔高差变化曲线
由图14可知,桥塔的高差对桥塔的竖向力有着显著的作用,由0 m增大到20 m,桥塔竖向力增加了4%到5%,使得全桥受力有了较明显的重分配趋势,较高侧桥塔的增加量明显大于较低侧主塔压力的减少量.由图15和图16可知,主缆对各支点的竖向压力的影响中,散索鞍和锚面处的影响缺十分有限.这两处的变化量主要来自于缆力变化的传递,也符合前文得出的结论,即主缆的边跨和锚跨主要来自于中跨受力变化的传递.
4不等高支承对主缆线形及无应力长度的影响
4.1不等高支承对主缆线形的影响分析
仅选取两侧桥塔高差为0,5,10,15,20 m 5种情形进行对比分析.见图17~18.

图17 特定高差下主缆线形对比图
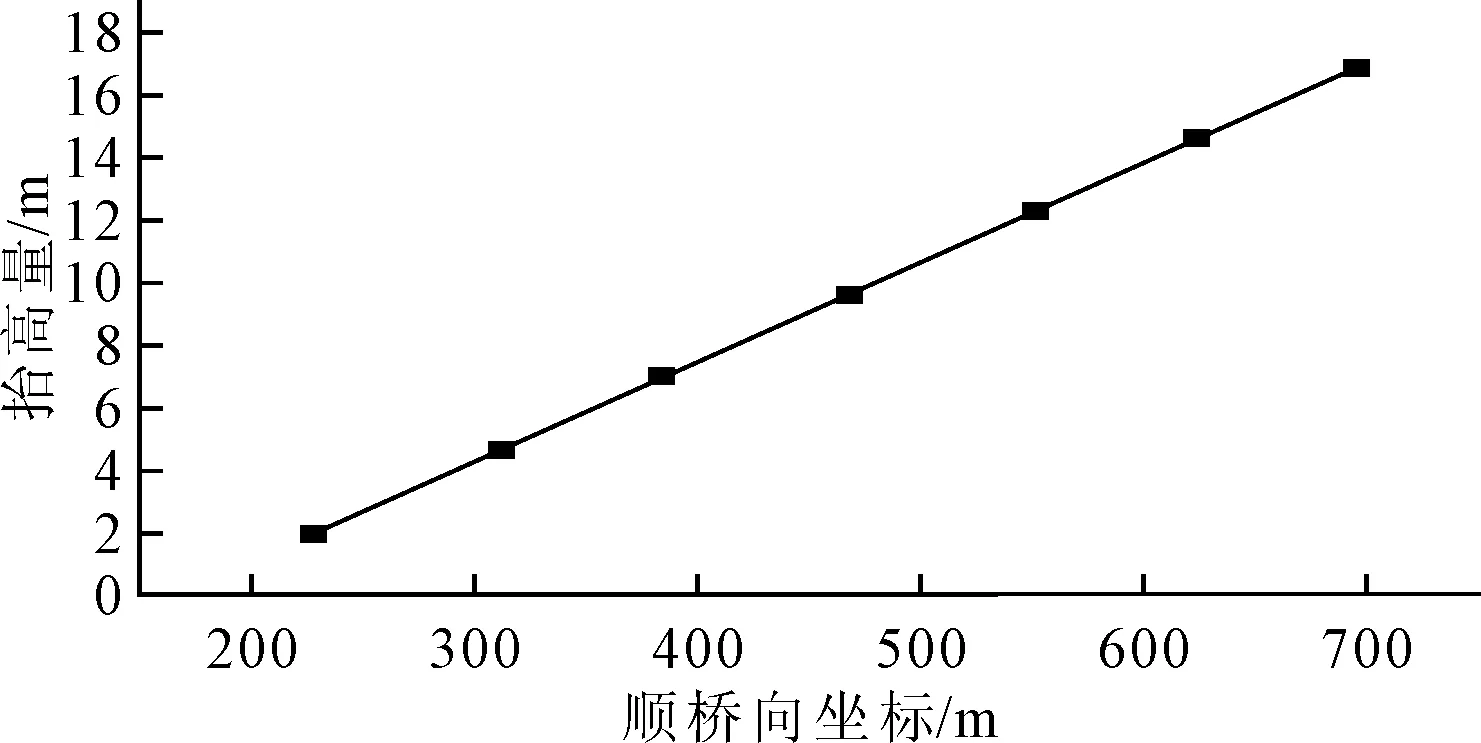
图18 中跨关键点抬高量
由图17分析可知,对左侧边跨的线形影响极小,而右边跨随IP点的提升有整体稳定提升的趋势,中跨整体悬链线最低点左移.从图18分析知,当桥塔从0 m到20 m抬高时,跨中关键点的抬高量大致呈线性提升,跨中点抬高量大致为塔高抬高量的一半.这个线形的偏移使得桥梁整体受力趋于不合理呈现出明显的不对称.
4.2不等高支承对索鞍左右切线角的影响分析
计算数据表明,当桥塔高差由0 m升至20 m时,左边索鞍左侧和右边索鞍右侧的切线角变化极小,在0.000 1°左右;左边索鞍右侧、左主索鞍左侧、右主索鞍右侧以及右边索鞍左侧的切线角增大量也都很小,在0.002°左右;但中跨2个的切线角即左侧主索鞍右侧及右侧主索鞍左侧,变化较为明显,变化量都在1.6°左右,高差每增大1 m,切线角变化量在0.08°左右.
4.3不等高支承对各跨主缆曲线长度及无应力长度的影响分析
对提取的各跨曲线长度及无应力长度数据,按索鞍细部修正后得最终结果.边跨和锚跨的变化量极小,2桥塔高差变化在20 m范围内时其量为毫米级,可以忽略不计.

图19 中跨主缆总长与桥塔高差拟合图
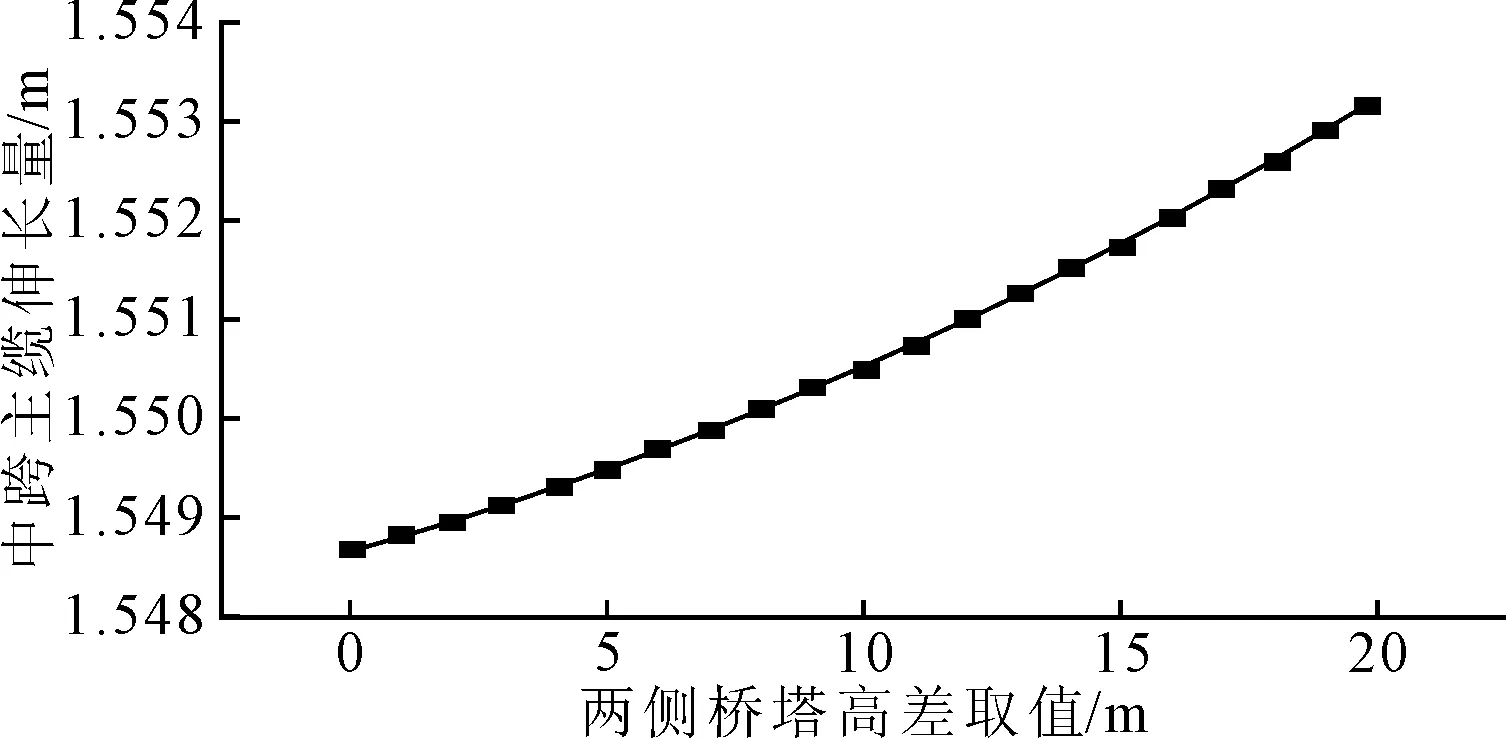
图20 中跨主缆弹伸长量与桥塔高差拟合图
而对中跨,主缆总长度值和主缆弹性伸长量变化则很明显,两者与2桥塔高差关系均大致为抛物线形式,故拟合曲线如图19和图20.
可见,随2桥塔高差增大,中跨主缆总长度和主缆的弹性伸长量的上升速度变快.总体来说,不等高桥塔增大了主缆的曲线长度和无应力长度,呈现抛物线曲线的增长趋势.这也验证了前文主缆受力的结论:随不等高桥塔取值的增加,主缆受力也越来越不利.
5结论
1) 主缆的受力上,主缆内力的变化随两桥塔高差变化呈线形变化,高塔侧受力大于低塔侧,且高塔侧的增加量大于低塔侧的减少量,引起了主缆内力的重分布,使得塔高侧区域缆力越为不利.
2) 各支点的竖向反力与主缆内力相似,随桥塔高差的变化有明显的影响.20 m高差范围内,变化幅值在4%到5%,塔高侧受力不利,散索面和锚面的竖向压力增量小,来自于缆力变化的传递.
3) 在主缆线形方面,右侧桥塔的增高,使线形最低点明显左移,呈现不对称趋势.跨中各点的抬高量沿顺桥向稳定抬升,跨中抬高量为塔高差的一半.
4) 切线角的变化方面,除中跨两切线角变化较明显外其余六个切线角变化极其微小,可忽略不计.
5) 对主缆的总长度和无应力长度而言,随塔高差增加呈现抛物线式的增长,上升速度随高差增加而变快,也反映出主缆受力随塔高差的增加而愈发不利.
参 考 文 献
[1]唐茂林,强士中,沈锐利.悬索桥成桥主缆计算的悬链线方法[J].铁道学报,2003(1):18-21.
[2]李传习.混合梁悬索桥非线性精细计算理论及其应用[D].长沙:湖南大学,2006.
[3]罗喜恒.复杂悬索桥施工过程精细化分析研究[D].上海:同济大学,2004.
[4]王雷,李传习.大跨度悬索桥主缆线形及内力计算方法研究[J].安徽建筑工业学院学报:自然科学版,2011(3):10-14.
[5]王晓明,郝宪武,石雪飞,等.特大跨悬索桥的缆索体系优化[J].昆明理工大学学报:理工版,2008(6):55-60.
[6]杨勇.非对称悬索桥主缆线形程序开发与参数分析[D].重庆:重庆交通大学,2010.
[7]何为.大跨径悬索桥施工监控中若干问题的研究[D].杭州:浙江大学,2006.
[8]叶志龙,王昌将,沈锐利,等.舟山西堠门主缆参数误差对施工线形影响的分析[C].中国公路学会桥梁和结构工程分会2007年全国桥梁学术会议,广州,2007.
[9]魏建东,刘忠玉.悬索桥结构分析中索鞍的精确模拟[J].工程力学,2006(7):114-118.
[10]唐茂林,沈锐利,强士中.悬索桥索鞍位置设计[J].公路交通科技,2001(4):55-57.
Research on the Infulence of Main Cable with
Unequal Height Support of Suspension Bridge
HE Yaobei1)DUAN Ruifang2)WANG Xiaoming3)
(TransportationPlanningSurveyandDesignInstitute
ofHunanProvince,Changsha410008,China)1)
(ShaanxiCollegeofCommunicationTechnology,Xi’an710018,China)2)
(InstituteofBridgeEng.,Chang’anUniv,Xi’an,710064,China)3)
Abstract:In order to study the influence of force and alignment of main cable with unequal height support, the finite element model was established aiming at the special suspension bridge with unequal height support, and the force and alignment of main cable was analysized. The key parameters of main cable was chosen, and the change data of each parameters was extracted and combined with the corresponding analytical calculation formula and detailed auxiliary correct calculation.Curve fitting results was studied and obained the influence of unequal height support. The results show that the unequal height support of main cable has the great effect of main cable, which leads to increase the internal force and reaction and offset the general alignment, especially the high tower side.
Key words:bridge engineering;suspension bridge; main cable; unequal height support; finite element method
收稿日期:2015-11-21
doi:10.3963/j.issn.2095-3844.2016.01.021
中图法分类号:U448.25
