考虑网络结构的航线客流重力预测模型*
2016-03-04张亚平郝斯琪
张亚平 彭 挺 郝斯琪
(哈尔滨工业大学交通科学与工程学院 哈尔滨 150090)
考虑网络结构的航线客流重力预测模型*
张亚平彭挺郝斯琪
(哈尔滨工业大学交通科学与工程学院哈尔滨150090)
摘要:为提高航线客流的预测精度,分别研究了城市间空间距离、节点度、平均路径长度、K-核、边介数和节点连通性对航线客流的影响,构建了考虑航线网络结构的航线客流重力预测模型,模型的预测精度达到了0.87,拟合优度较好.结果表明,城市间的空间距离对航线客流的影响具有两重性;两城市的节点度越大,其对应的每条航线可能分担的客流比例就越小,它们之间的交通阻抗也越大;航线的边介数不是航线客流的关键影响因素;平均路径长度、K-核和节点连通性显著影响航线客流,但与节点度、空间距离等存在多重共线性.
关键词:航空运输;航线客流;重力模型;网络结构;影响因素;预测模型
张亚平(1966- ):男,博士,教授,主要研究领域为交通规划与设计、交通流理论、民航资源配置等
*国家自然基金民航联合研究基金项目“民用机场航站楼资源动态分配与智能化调度基础理论研究”(批准号:61179069)、“飞机推出控制博弈机理模型与算法研究”(批准号:U1233124)资助
0引言
随着我国社会经济发展和人民生活水平的不断提高,民航旅客运输业发展迅猛,国内航线条数由1999年的987条增加到2014年的3 142条,民用机场也由132个增加到202个,并且还将继续保持快速增长的趋势.为合理安排机场和航线的开通计划,保证新增机场和航线的运行效益,需要对航线客流进行科学合理的预测.
目前,国内外相关学者对航线客流的预测方法进行了深入研究,并取得了丰硕成果.对于已开通航线,一般采用时间序列分析法.何冬昀等[1]提出了航线客流需求预测的改进Winters方法.景崇毅等[2]基于预测结果的残差序列对ARIMA模型进行了二次建模,提高了模型的预测精度.除此之外,齐禺萌[3]采用灰色系统理论对航线客流的预测问题展开了研究.孙宏等[4]认为两个城市之间的航空客货需求量与GDP成正比,而与空运运价成反比,并基于某条航线的历史数据,构建了航线客流的广义重力预测模型.陈亚青等[5]基于系统动力学构建了航空客流预测模型,并对模型进行了有效性检验.
对于还未开通的航线,一般采用多元回归分析法.张桥艳等[6]采用人均GDP、第三产业增加值、财政支出、机场旅客吞吐量等指标,基于主成分分析法研究了航线客流的预测模型.张永莉等[7]选取GDP、年末总人口、土地面积、旅客吞吐量等社会经济指标,考虑航线距离和航线类型,运用半对数线性模型对城市间的航空客流进行了回归分析.不少学者还借鉴重力模型展开了深入研究,并认为航线客流由地理经济和设施供给两方面的相关指标决定[8].其中,社会经济指标多采用城市人口、购买力指数、GDP、全职员工人数、就业组成及城市类型等[9-10];空间地理指标一般采用城市间的距离;设施供给指标一般考虑航班班次、飞机类型、票价等[11-14].除此之外,还有学者采用逆向重力模型研究了机场旅客吞吐量与城市间民航客流的关系[15-16],具有一定的借鉴意义.
现有的相关研究成果丰硕,涵盖面较广,具有较高的参考价值,但还存在某些不足,主要表现在:时间序列分析法仅适用于已开通航线,不能预测未开通航线的客流;采用重力模型或多元回归分析法对航线客流进行预测时,所选用的各个指标之间往往存在相关性,影响预测结果的可靠性;相关研究较少考虑航线网络结构的影响,研究结果的适用范围受到限制;航班班次、座位数等供给指标对航线客流的影响还存在争议.
针对现有研究存在的不足,文中基于经典的重力模型,考虑航线网络结构的影响,梳理航线客流的影响因素及影响因素之间的关系,构建航线客流的重力预测模型.文中研究结论有助于加深对航线客流分布的认识,提高航线客流的预测精度,从而指导航空公司科学合理地拟定航线开通计划,并为民航管理部门制定有关的引导策略提供参考.
需要说明的是,文中仅研究直达航线的客流预测方法,同时将城市(而非机场)作为航线的节点.因此,文中所研究的航线客流实际为城市对之间的民航客流.此外,文中以课题组所掌握的2010年中国国内航线拓扑网络为研究基础.
1初步的航线客流重力预测模型
根据牛顿的万有引力定律,两物体之间的引力与它们的质量的乘积成正比,而与它们之间的距离成反比.改进的引力模型(或重力模型)在地理、经济、交通、贸易等领域得到了广泛的应用.在交通规划中,其可以表示为[17-19]
(1)
式中:Tij为区域i与区域j之间的交通量;K,α,β为待定常量;Mi和Mj分别为区域i的交通产生量和区域j的交通吸引量;f(Dij)为交通阻抗函数值,其值越大,说明交通阻抗越小,Dij一般用时间或距离表示.
从年鉴《从统计看民航》(2011)提取2010年各民用机场的旅客吞吐量数据,整理得到每个城市对应的民航旅客吞吐量,并将其作为重力模型中的交通产生量和吸引量.同时,获取各个民用机场的经纬度数据,按照式(2)计算任意2个城市之间的空间距离.对于拥有多个机场的城市,文中计算这些机场的中心点对应的经纬度.
Lij=R·arccos(cos(lati·π/180°)·
cos(latj·π/180°)·cos(lngi·π/180°-
lngj·π/180°)+sin(lati·π/180°)·
sin(latj·π/180°))
(2)
式中:Lij为城市i和城市j之间的空间距离,km;R为地球半径,取6 370 996.81 km;lngi和lati分别为城市i的经度和纬度.
一般地,区域i与区域j之间的交通阻抗函数值f(Dij)可以用空间距离的幂函数、指数函数和Gamma函数来计算.因此,文中分别采用这三个函数,初步构建航线客流的重力预测模型,结果如下所示:
式中:Pij为城市i和城市j之间的航线客流,万人次;Ti,Tj为城市i和城市j对应的民航旅客吞吐量,万人次;Lij为城市i和城市j之间的空间距离,100 km.
由式(3)~式(5)可以看出,采用重力模型的拟合效果较好,3个模型的可决系数均超过0.85,各个参数均通过了t检验.同时,采用空间距离的幂函数和指数函数构建重力模型时,空间距离Lij对应的参数均小于0,说明从整体上来看,两城市之间的空间距离越远,对应的民航旅客出行阻抗越大.但是,由式(5)中Gamma函数的各个参数的标定值可以看出,当两城市间的空间距离较近时,随着距离的增加,交通阻抗反而减小.
若考虑民航与公路、铁路等其他运输方式之间的竞争关系,当两城市之间的空间距离较近时,民航旅客运输的优势将随着距离的减小而不断减弱.因此,文中认为采用空间距离的Gamma函数构建重力预测模型更符合实际情况,即公式(5)为本文初步构建的航线客流重力预测模型.
2航线网络结构的影响分析
航线客流包括2部分:以该航线对应的两个城市为起终点的OD客流;途经该航线的中转客流.
居民出行的起讫点一般不受航线网络分布、航班计划等因素的影响,而主要由居民自身的出行目的决定.同时,OD客流的出行距离往往呈现出一定的概率分布特征.因此,对于OD客流而言,城市的地理位置(或城市之间的空间距离)对其出行行为的影响较为明显.
若某条航线位于网络的中心位置,旅客通过该条航线可以很方便地到达其他城市,那么该航线一般会承担大量的中转客流.以乌鲁木齐至北京的直达航线为例,2010年新疆维吾尔自治区境内12个通航城市的旅客均需借助该航线才能较为方便地到达华北和东北地区.虽然该航线对应的飞行距离较长,但特殊的网络结构决定了其不仅承担了乌鲁木齐与北京之间的OD客流,还承担了大量的中转客流.因此,对于中转客流而言,航线网络结构对其出行行为的影响更为突出.
综合以上分析,航线客流大小不仅受通航城市地理位置的影响,还在很大程度上受到航线网络结构的制约,尤其是中转客流较大的干线.然而,文中初步构建的航线客流重力预测模型(见公式(5))仅考虑了城市地理位置的影响.因此,还需要在系统分析航线网络结构对航线客流的影响基础上,对初步构建的航线客流重力预测模型进行改进.
2.1节点度的影响
文中所研究的航线网络以中国国内2010年夏秋季各个机场的航班时刻表为准,研究范围不包括台湾、香港和澳门地区.同时,以城市为节点,若两城市间有直达航线,则视它们为邻接节点,否则两节点不邻接.按此方法,文中构建2010年中国国内航线网络的邻接矩阵.
节点度为网络的一个重要指标,节点i的度Di定义为该节点所有邻接节点的数目.一个节点的度值越大意味着其在某种意义上越“重要”.当城市的民航旅客吞吐量一定时,节点度Di越大,其邻接城市就越多,对应的每条航线可能分担的客流比例就越小.
文中计算各节点(城市)的度值,并分别用两城市节点度的加法形式和乘法形式代替公式(5)中的交通阻抗函数,构建航线客流重力预测模型,结果如下所示:
(6)
(7)
式中:Di,Dj为城市i和城市j的节点度.
可以看出,无论是采用加法形式还是乘法形式,在所构建的重力模型中,节点度对应的参数均为负值.说明两城市的节点度越大,它们之间的交通阻抗越大,这与前面的定性分析结果是一致的.
2.2平均路径长度的影响
平均路径长度是网络的另一个重要指标.网络中节点i和节点j之间的最短路径长度PLij定义为它们之间的最短路径对应的边数目,某节点的平均路径长度PLi定义为该节点与其他所有节点之间的最短路径长度的平均值,即
(8)
式中:N为网络中节点数.
文中采用复杂网络软件Pajek计算各个节点对应的平均路径长度.分别用平均路径长度的加法形式和乘法形式代替式(5)中的交通阻抗函数,构建航线客流重力预测模型,结果如下所示.
(9)
(R2=0.838 2)
(10)
可以看出,无论采用加法形式还是乘法形式,平均路径长度对应的模型参数均大于0,说明2城市的平均路径长度越大,它们之间的交通阻抗越小.实际上,若某城市的平均路径长度较大,表明其与其他城市之间的航线联系较弱,对应的民航旅客仅能通过少数几条航线达到出行目的,因此该城市对应的航线可能分担较大比例的客流,这与节点度对航线客流的影响十分类似.平均路径长度与节点度的统计关系见图1,两者之间存在显著的负相关关系,这也是重力预测模型中平均路径长度对应的参数为正值而节点度对应的参数为负值的原因.

图1 平均路径长度与节点度的关系
2.3K-核的影响
若一个网络的最大全连通子网包含有K+1个节点,则该网络为K-核网络.同时,如果网络中的一个节点存在于某个K-核子网中,而不存在于任何一个(K+1)-核子网中,则该节点的核为K.K-核体现了一个节点在网络中的深度,也反映了其在网络中的地位.与前面的分析方法类似,文中采用复杂网络软件Pajek计算各个节点的核,并分别用两个城市K-核的加法形式和乘法形式代替式(5)中的交通阻抗函数,构建航线客流重力预测模型,即:
(R2=0.837 7)
(11)
(R2=0.769 1)
(12)
式中:Ki,Kj为城市i和城市j的核.
与前2个影响因素的分析结果不同,当采用K-核的加法形式时,K-核对应的回归系数为负值,但是采用乘法形式时,回归系数大于1.比较两个模型的拟合优度,采用加法形式的模型拟合效果更好.与此同时,K-核与节点度存在明显的相关关系,见图2.除少数几个枢纽节点的K-核保持不变以外,其他节点的K-核与节点度呈现出线性正相关关系.因此,K-核对航线客流的影响应与节点度类似.也就是说,当民航旅客吞吐量一定时,某城市的K-核越大,其对应的航线可能分担的客流比例应越小.

图2 K-核与节点度的关系
2.4边介数的影响
在复杂网络理论中,边介数定义为网络中所有最短路径中经过该条边的数目,其反映了一条边在整个网络中的作用和影响力.某条航线的边介数越大,说明其在网络中的集散功能越显著.文中采用R软件的igraph工具包计算各条航线对应的边介数,并用来代替式(5)中的交通阻抗函数,构建航线客流重力预测模型,即
式中:Eij为城市i和城市j对应航线的边介数.
在所构建的重力模型中,边介数对应的参数为正值,说明边介数越大,节点之间的交通阻抗越小,这符合实际情况.但是,解释变量边介数并未通过t检验,说明边介数并不显著影响航线客流.
2.5节点连通性的影响
两个节点间的连通性(简称为节点连通性)定义为截断两节点间的联系需删除边的最少条数.本文利用社会网络软件Ucinet计算节点连通性,并用来代替公式(5)中的交通阻抗函数,构建航线客流重力预测模型,结果如下.
(14)
式中:Cij为城市i和城市j之间的节点连通性.
在所构建的重力模型中,节点连通性对应的参数为负值,说明节点连通性越大,它们之间的交通阻抗越大.实际上,节点连通性越大,可供旅客选择的出行路径条数越多,对应航线分担的中转客流就越少.同时,解释变量通过t检验,说明节点连通性显著影响航线客流.
3改进的航线客流重力预测模型
根据前文的分析可知,航线客流不仅受城市间空间距离的影响,还与航线网络结构密切相关.在文中提出的反映航线网络结构的5个指标中,除边介数以外,其余4个指标均显著影响航线客流.考虑到各个指标之间的相关性,尤其是节点度、平均路径长度、K-核三者之间表现出的强相关性,文中采用逐步回归法对初步构建的航线客流重力预测模型进行改进.
首先,在式(5)的基础上,分别引入节点度、平均路径长度和K-核3个指标,得到改进的航线客流的重力预测模型如下.
(17)
重新构建的3个重力预测模型的拟合优度均略有提高.但是,在5%的显著性水平条件下,平均路径长度和K-核两个变量均未通过t检验,说明式(16)和式(17)中的各个变量之间存在相关性.同时,对比3个模型的拟合优度,文中建议在初步构建的重力预测模型中引入节点度指标.
然后,在式(15)的基础上,引入节点连通性指标,再次改进航线客流的重力预测模型,结果如下.
(18)
引入节点连通性指标后,模型的拟合优度并没有明显的提高,节点连通性也未通过t检验,说明新增加的模型变量对航线客流的影响不显著.然而,根据式(14),节点连通性指标显著影响航线客流,2个分析结果似乎互相矛盾.事实上,式(18)在式(14)基础上增加了空间距离这一指标,若空间距离在一定程度上与节点连通性相关,且前者对航线客流的影响相对于后者更显著,则必然会出现以上情况.
综上所述,式(15)为文中所改进的航线客流重力预测模型.基于该模型,对2010年中国国内各条航线的客流进行预测,预测的平均精度达到了87%(如式(15)所示,R2=0.870 3),在可接受范围内.各条航线的预测结果见图3.
将文中所提出的航线客流重力预测模型应用于实际时,可先收集各个通航城市民航旅客吞吐量的现状数据,然后对重力预测模型中的各个参数进行标定.最后,根据标定后的重力预测模型,即可粗略预测拟开通航线的潜在客流量.在此基础上,对机场吞吐量进行修正,并根据重力模型重新预测拟开通航线的潜在客流量,从而为航空公司制定航线开通计划提供参考.
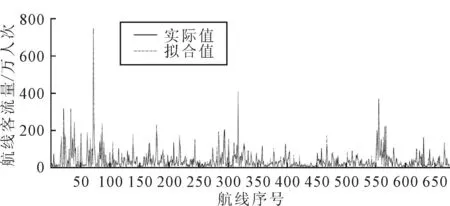
图3 各条航线客流量预测结果
4结论
1) 整体而言,两城市间的空间距离越远,对应的民航旅客出行阻抗越大.当两城市间的空间距离较近时,随着距离的增加,民航旅客出行的阻抗反而减小.
2) 当城市的民航旅客吞吐量一定时,2城市的节点度越大,对应航线可能分担的客流比例就越小,它们之间的交通阻抗也越大.
3) 航线的边介数不显著影响航线客流,而节点连通性是航线客流的一个关键影响因素.节点连通性越大,可供旅客选择的出行路径条数越多,对应航线分担的中转客流就越少.
4) 文中所提出的航线客流重力预测模型的预测精度能够达到87%,满足实际使用需要.
受基础数据的限制,文中未对重力预测模型的参数进行稳健性分析,未来有必要根据历史数据对此进行验证.除此之外,实际中的航线可能由多个航段组成,多条航线也可能通过同一航段,文中仅研究了直达航线的客流量预测方法,下一步还需要考虑其是否包含经停点、是否存在多条航线在同一航段上竞争的情况等,更深入地研究航线客流的预测方法.
参 考 文 献
[1]何冬昀,罗利.航线需求预测的一种改进Winters方法[J].交通运输系统工程与信息,2006(6):103-107.
[2]景崇毅,周慧艳,石丽娜.基于ARIMA模型的残差修正的航线运量预测方法[J].工业工程,2010,13(1):74-79.
[3]齐禺萌.基于灰色系统理论的航空运量预测[J].航空运输,2008,86:66-67.
[4]孙宏,史虹圣.航线运输需求量预测模型研究[J].中国民航飞行学院学报,2004,15(4):38-40,43.
[5]陈亚青,韩云祥.基于系统动力学的航空系统客运量预测模型[J].交通信息与安全,2009,27(5):146-148,165.
[6]张桥艳,熊越强.航线客运量影响因素分析及预测[J].桂林航天工业学院学报,2012(4):364-366.
[7]张永莉,张晓全.我国城市间航空客运量影响因素的实证分析[J].经济地理,2007,27(4):658-660,671.
[8]RENGARAJU V R, THAMIZH A V. Modeling for air travel demand[J]. Journal of Transportation Engineering, 1992,118(3):371-380.
[9]JORGE-CALDERON J D. A demand model for scheduled airline services on international European routes[J]. Journal of Air Transport Management,1997,3(1):23-35.
[10]Grosche T, Rothlauf F, Heinzl A. Gravity models for airline passenger volume estimation[J]. Journal of Air Transport Management,2007,13(4):175-183.
[11]GARDNER J, EVERETTE S. Dimensional analysis of airline quality[J]. Interfaces,2004,34(4):272-279.
[12]GURSOY D, CHEN M H, KIM H J. The US airlines relative positioning based on attributes of service quality[J]. Tourism Management,2003,26(1):57-67.
[13]LEE D. Concentration and price trends in the US domestic airline industry: 1990-2000[J]. Journal of Air Transport Management,2003,9(2):91-101.
[14]PARK J W, ROBERTSON R, WU C L. The effect of airline service quality on passengers’ behavioural intentions: a Korean case study[J]. Journal of Air Transport Management,2004,10(6):435-439.
[15]刘晓明,夏洪山.基于逆向重力模型的枢纽机场旅客吞吐量估计方法[J].交通运输工程学报,2008,8(2):85-89.
[16]SHEN G Q. Reverse-fitting the gravity model to inter-city airline passenger flows by an algebraic simplification[J]. Journal of Transport Geography,2004,12(3):219-234.
[17]王炜,陈学武.交通规划[M].北京:人民交通出版社,2007.
[18]钱江海,韩定定.基于预期流优化的空间网络引力模型[J].物理学报,2009,58(5):3028-3033.
[19]江小帆,李翔,陈关荣.复杂网络理论及其应用[M].北京:清华大学出版社,2006.
Gravity Model for Forecasting Airline
Passenger Flow Considering Network Structure
ZHANG YapingPENG TingHAO Siqi
(SchoolofTransportationScienceandEngineering,
HarbinInstituteofTechnology,Harbin150090,China)
Abstract:In order to improve the precision of airline passenger flow prediction, the effects of spatial distance between cities, degree, average path length, k-core, edge betweenness and point connectivity on airline passenger flow are explored. And then, a gravity model for forecasting airline passenger flow is constructed. Prediction accuracy of the gravity model proposed in this study reaches 0.87, so the goodness of fit is acceptable. The results indicate that the influences of spatial distance on airline passenger flow have a characteristic of duality. The greater the degrees of two cities are, the smaller the proportions of passenger flows corresponding to each airline are, and the greater the traffic impedance between them is. Edge betweenness is not the key factor affecting airline passenger flow. Moreover, Average path length, k-core and point connectivity significantly affect airline passenger flow, but there is multicollinearity between these indicators and spatial distance (or degree).
Key words:air transportation; airline passenger; gravity model; network structure; influence factor; prediction model
收稿日期:2015-07-28
doi:10.3963/j.issn.2095-3844.2016.01.003
中图法分类号:F562.8
