独塔斜拉桥钢拱塔竖转施工稳定性分析及对策研究*

王向阳　夏小勇　韩丽丽

(武汉理工大学交通学院　武汉　430063)



独塔斜拉桥钢拱塔竖转施工稳定性分析及对策研究*

王向阳夏小勇韩丽丽

(武汉理工大学交通学院武汉430063)

摘要：针对独塔斜拉桥钢拱塔竖转施工过程中竖转体系的稳定性问题，以武汉市高新二路独塔斜拉桥为研究背景，介绍了一种竖转架和钢拱塔相结合的双向牵引的自平衡竖转体系.利用通用有限元分析软件ANSYS建立独塔斜拉桥全桥模型，并在此基础上对独塔斜拉桥进行了稳定性计算分析.计算结果表明，在竖转施工过程中该竖转体系不会产生第一类和第二类失稳现象.最后，提出了两条增强该竖转体系稳定性的措施，以确保竖转施工安全顺利地进行和独塔斜拉桥的正常使用.

关键词：独塔斜拉桥；竖转施工；稳定性分析；钢拱塔；竖转架

王向阳(1971- )：男，博士，教授，主要研究领域为桥梁结构

*湖北省自然科学基金面上项目资助(批准号：2013CFB342)

0引言

斜拉桥钢拱塔竖转施工是近年来刚刚兴起的一项施工技术，采用整体竖转的施工方法进行钢拱塔的吊装，可降低钢拱塔结构的高空拼装工作难度，使钢拱塔最终安装精度得到了有效的保证.但这项新兴的施工工艺也面临着不小的施工挑战：施工过程中竖转体系的稳定性难以得到保证,竖转到位后因拱脚变形而导致的焊接困难,等等.以往的工程实例中，为了保证竖转体系的稳定性而采取的措施一般是增大结构的断面尺寸,以及采用大型吊装设备辅助竖转.这些方法无疑会增大结构自重，增加工程造价.

文中以武汉市高新二路独塔斜拉桥为研究背景，结合工程实践提出了一种竖转架和钢拱塔结合的双向牵引竖转施工装置，并对该竖转体系进行稳定性计算分析，计算结果表明,该装置能保证竖转施工过程中竖转体系的稳定性，同时也能达到保证施工安全、提高施工质量、节省施工成本的目的.

1工程概况

武汉市高新二路在《武汉科技新城总体规划(修编)2005～2020》中被定性为生活性城市主干路，桥梁工程起于规划十二路交叉口，自西向东依次跨越神墩一路、外环路，止于规划上大路交叉口，形成高新二路高架桥.

高架桥桥跨布置为3×30 m(预应力混凝土连续箱梁)+30 m+32 m+54 m+32 m+30 m(预应力混凝土箱梁)+65 m+95 m(钢箱梁独塔斜拉桥)+3×30 m(预应力混凝土连续箱梁).高架桥主桥为独塔双索面独塔斜拉桥，桥跨布置为:65 m+95 m，主梁采用钢箱梁结构，梁高2.6 m；塔高66.1 m，主塔尺寸3.6 m×3.6 m，主塔外观横立面看呈斜伸的网球拍形，与竖直方向立面呈10°的倾斜角.

由于特殊的结构造型及现场施工条件的限制，钢拱塔的安装无法采用常规吊装方法进行施工.结合工程实际，采用整体竖转的施工方法进行斜拉桥钢拱塔的吊装，实际工程中，钢塔从初始位置(与平面成15°夹角)竖转至目标位置(与平面成80°夹角)是一个连续的动态过程，文中选取了5个静态工况，通过其变化趋势来模拟这一竖转过程.根据设计资料，将该施工过程分为以下5个工况：钢塔竖转初始工况(15°工况)、钢塔竖转中间工况(30°工况)、钢塔竖转中间工况(45°工况)、钢塔竖转中间工况(60°工况)、钢塔竖转完成工况(80°工况).

钢拱塔结构在竖转过程中受到重力及两根牵引索的拉力作用会产生变形.拉索的拉力可以分解为垂直钢拱塔方向和顺塔方向的2个力，垂直钢拱塔方向的力使钢拱塔沿拱脚提升，而顺塔方向的力则会使钢拱塔产生竖向变形甚至发生屈曲.计算得到钢拱塔产生线性屈曲的荷载值为1.63×108N.实际竖转过程中，钢拱塔承受的最大竖向荷载为3.59×106N.

该竖转体系主要包括：钢拱塔、竖转架、钢箱梁、竖转铰、防滑移支座、竖转架铰座、前拉索、后拉索、平衡索和稳定索，见图1.前拉索一端连接钢拱塔前拉索锚点，另一端连接竖转架前端耳板；后拉索一端连接竖转架后端耳板，另一端通过连接钢箱梁后拉索锚；平衡索一端连接钢拱塔平衡索锚点，另一端连接钢箱梁平衡索锚点；稳定索通过稳定索连接件安装在钢拱塔稳定索锚点上.钢拱塔、竖转架和前后拉索是本次竖转施工采用的双向牵引竖转体系的重要组成部分，其稳定性直接关系到施工过程的安全性.

目标指引行动。“让台州人民更健康，为人类健康事业做贡献”是恩泽集团的使命，“成为中国医疗卓越运营的典范”是集团愿景。在综合目标指引下，陈海啸将其解构分类齐全，从而确立了“患者感知-安全与质量-员工学习与成长-财务平衡四个维度”的集团运行“真北”。

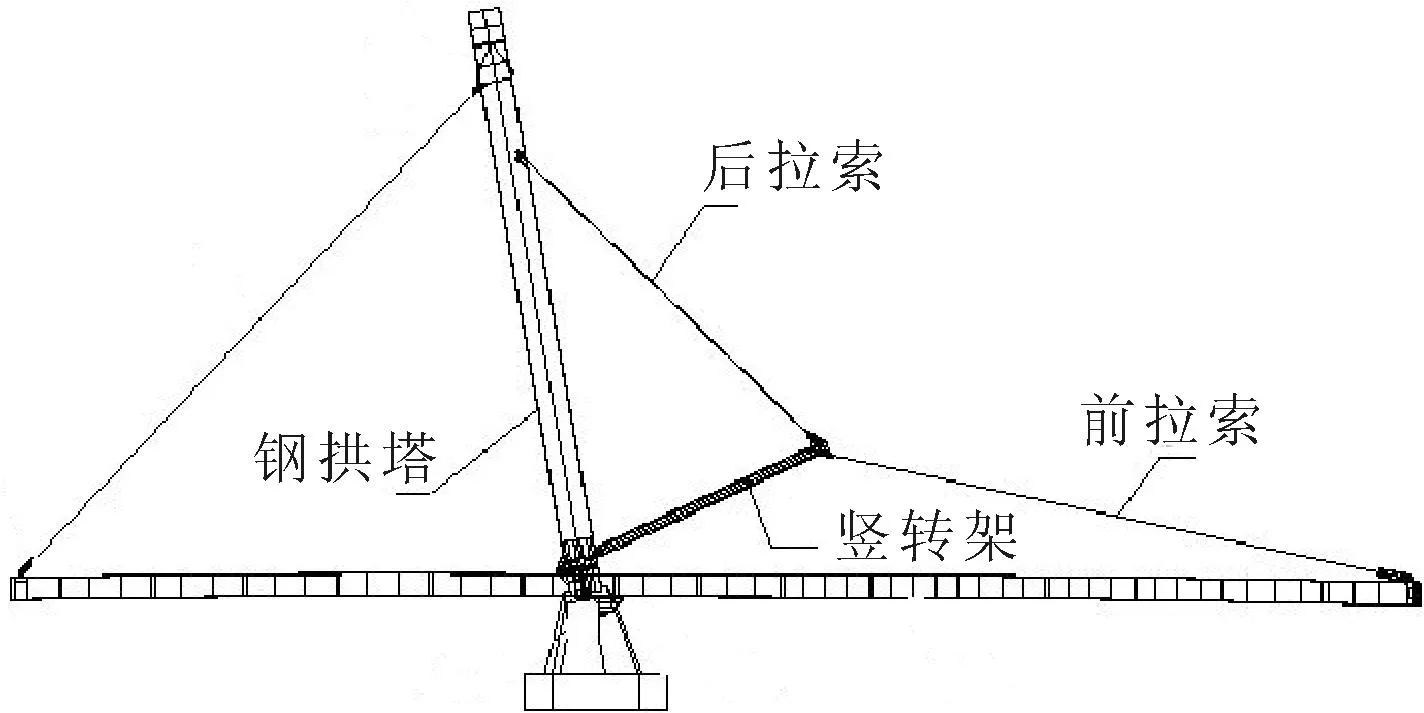
图1　双向牵引的竖转体系

2竖转体系稳定性分析的有限元方法

根据失稳的性质，结构稳定性问题可以分为以下3种.第一种是荷载达到某个值时，除了结构原来的平衡状态外出现了第二个平衡状态，故又称为分枝点失稳，这类问题在数学上处理为求解特征值问题，故又称为特征值屈服分析.第二种是结构失稳时，变形将大大发展，而不会出现新的变形形式，即平衡状态不发生质变，也称为极值点失稳[2]，结构失稳时，相应的荷载称为极限荷载.大多数结构的失稳问题属于第二类失稳问题.第三种是当荷载达到某个值时结构平衡状态发生跳跃，突然过渡到另一个具有较大位移的平衡状态，也称跳跃失稳.

接着对竖转体系进行非线性稳定分析，计算过程主要是通过不断的试算，调整施加荷载的大小，最终求得结构达到塑性极限状态时荷载的大小及发生塑性变形的区域.

2.1计算理论

为了验证竖转体系的稳定性，采用通用有限元分析软件ANSYS，用梁单元模拟钢箱梁、钢塔及竖转架，桁架单元模拟斜拉索，建立了钢塔竖转施工各工况下的独塔斜拉桥上部结构有限元模型，见图2.在已建立的有限元模型基础上对竖转体系完成工况进行稳定性计算分析[5-8].

第二类和第三类失稳问题，在ANSYS中对应的是非线性分析.非线性稳定分析采用一种逐渐增加荷载的办法来求得使结构开始变得不稳定时的临界荷载，它是在大变形效应开关打开(NL- GEOM,ON)的情况下所做的一种静力分析，该分析过程一直进行到结构的极限荷载.分析过程中可包含塑性等非线性选项.非线性稳定分析考虑了结构的初始缺陷，结果比特征值屈曲分析精确，常用于对实际结构进行分析、设计.

第四，研究前沿时序图谱表明，政府机构改革前沿主题较多，学科交叉特征十分明显，前沿量化研究方法正在该领域盛行。“政治体制改革”“政府机构设置”“行政管理”“管理体制改革”“机构编制”等热词开始进入政府机构改革的研究领域，推动本课题的研究往纵深方向发展。

现有一段全长43.34km的高速公路，其上层结构为4cm厚的细粒式改性沥青混凝土，中间结构为6cm厚的中粒式改性沥青混凝土，总厚度为10cm。

2.2独塔斜拉桥的有限元模拟

对于第一类失稳问题采用结构弹性稳定分析，目的是求解临界荷载，在ANSYS中对应的是特征值屈曲分析.特征值屈曲荷载是预期的非线性屈曲荷载的上限，特征值矢量屈曲形状可作为非线性屈曲分析时施加初始缺陷或扰动荷载的依据，预先进行特征值稳定分析有助于非线性屈曲分析[3-4].

图2　独塔斜拉桥全桥有限元模型

3稳定性计算结果及分析

经过特征值屈曲分析，提取独塔斜拉桥完成工况的前15阶固有频率和振型，见表1.

由表1可见，该独塔斜拉桥的基本周期为2.201 6 s，比其他漂浮体系的斜拉桥短，这与其墩、梁、塔刚构的体系有关，其第1阶频率明显低于第2阶频率，也与该桥的体系有关；该独塔斜拉桥左右跨跨径不同，这种不对称在振型中有明显体现；主梁截面抗扭惯矩比钢拱塔、竖转架大，故在第4振型和第5振型出现了钢塔、竖转架扭转；在前10阶振型中钢塔、竖转架出现弯曲和扭转的频率较高，其刚度值得注意.

表1　独塔斜拉桥自振频率和振型

图3为竖转架第一阶屈曲模态，计算得到，竖转架产生线性屈曲的荷载约为6.30×107N.实际竖转过程中，竖转架承受的最大压力为2.74×106N.

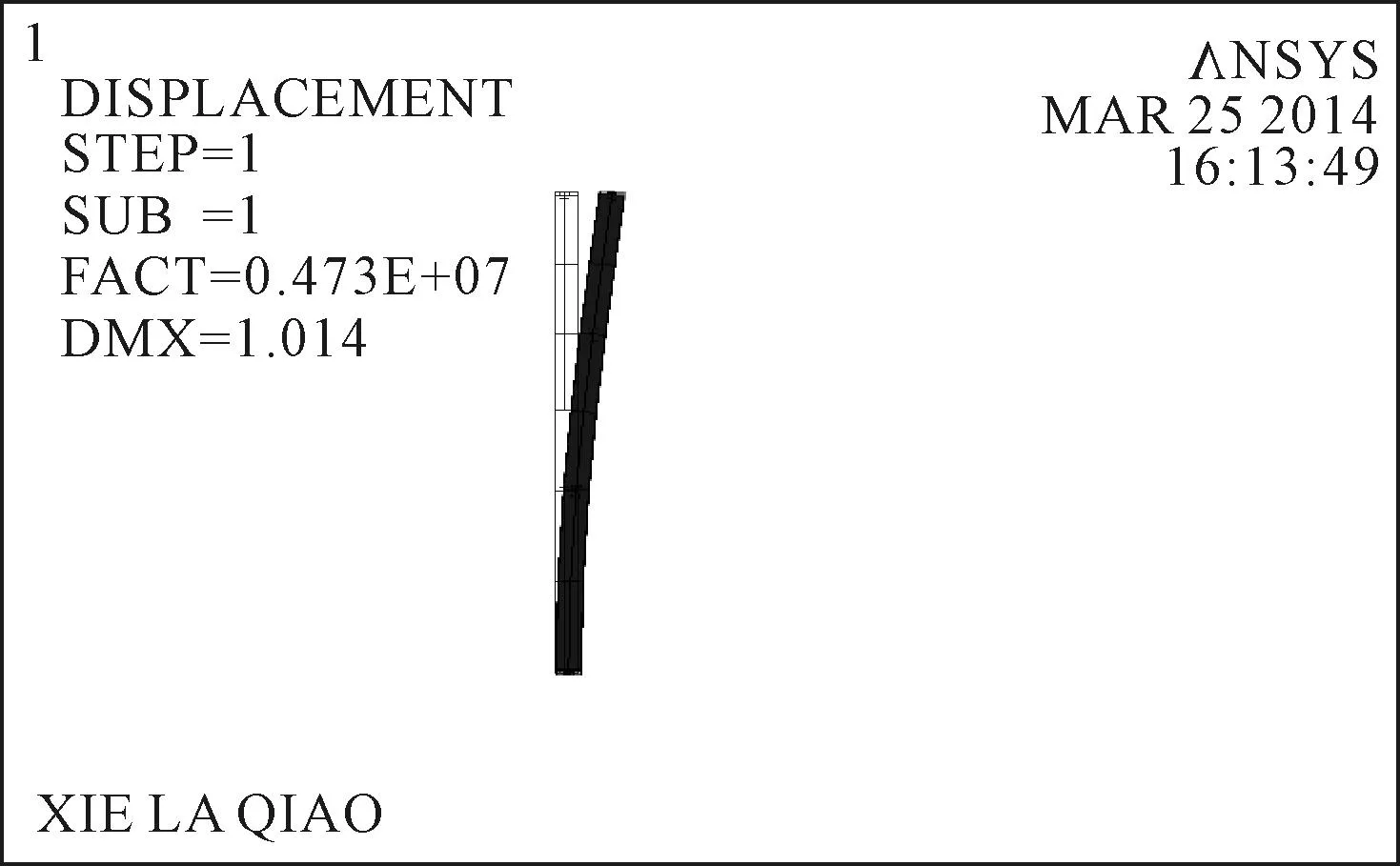
图3　竖转架第1阶屈曲模态

从全固态离子选择性电极信号传递原理看，固体接触材料除了可利用纳米材料较大电容性在离子选择膜和电子导体之间发挥离子到电子传导作用外，还可以借助疏水的导电高分子材料通过发生氧化还原反应(或掺杂反应)将扩散到电极的离子转化为电子，继而通过导电基底。

由特征值屈曲分析计算结果可以看出：在整个体系中，竖转架和钢拱塔的稳定性较其他部位更差；竖转架特征值屈曲分析的稳定安全系数为23.0，钢拱塔特征值屈曲分析的稳定安全系数为45.4，稳定安全系数表明，竖转架和钢拱塔不会发生第一类失稳；在竖转过程中，竖转架外侧下部杆件发生失稳和破坏的风险高于其他部位，在竖转架制作拼接过程中应格外注意该部分的施工质量.

结构在荷载作用下由于材料的弹性性能而发生变形，若变形后结构上的荷载保持平衡，这种状态成为平衡状态.对于在某一荷载作用下处于平衡状态的结构，当荷载达到某一值时，若增加一个微小增量，则结构的平衡位形发生很大变化，结构由原平衡状态经过不稳定的平衡状态而达到一个新的稳定的平衡状态[1]，这一过程就是失稳或屈曲.

由试算结果，当荷载超过8.00×106N 时，竖转架位移会无限增大，不再收敛，说明竖转架的塑性极限荷载为8.00×106N.竖转施工过程中，竖转架承受的最大压力为2.74×106N.图4是竖转架等效塑性应变云图，随着荷载的不断增加，竖转架的外侧杆件的下部最先发生塑性破坏.图5为钢塔塑性极限变形图.

图4　竖转架等效塑性应变云图

图5　钢塔塑性极限变形图

对钢拱塔，其塑性极限荷载值为4.80×107N.实际竖转过程中，竖转架承受的最大压力为3.59×106N.

由非线性分析计算结果可知,竖转架稳定安全系数为2.9，钢拱塔稳定安全系数为13.4，稳定安全系数表明，竖转架和钢拱塔不会发生第二类失稳.

以堤防、涵闸、泵站、灌区为主体的水利风景区等都属于此类。工程型水利风景区相对于水库型限制条件较少，尤其是对水质要求较低。因此，一方面可以沿堤观赏江河两岸宜人的自然风光，另一方面可在特定区域开展一些水上休闲娱乐等项目。但需注意，应该避免在泄洪区域修建相关设施，应选取坝上作为活动区域，并注意洪区季节性的影响，与周边度假区配合，保证淡季游客流量。

4增强结构稳定性的对策

见图6，在D3节段第二处隔板处增加2个钢绞线锚座，每束钢绞线由14根预应力钢绞线组成，初始张拉索力为单根40 kN，单根钢绞线束索力560 kN，总索力1 120 kN.竖转张拉开始后，待后拉索(提升钢绞线束)载荷达到1/2额定载荷时，开始张拉稳定索.稳定索采用100 kN张拉千斤顶单根张拉，尽量保证索力均匀.竖转完成后，稳定索将会拆除.

4.1安装稳定索

作为控制拱脚处应力和位移的关键装置，稳定索的安放位置既要保证索力的充分利用，又要防止稳定索释放后钢拱塔因振动而产生的横桥向失稳.索力的选用根据钢拱塔在拱脚产生的横向推力估算，应保证钢拱塔竖向转体就位后拱脚处的横向水平位移为零.

正当的法律程序可以给行政主体和行政相对人以正当的约束和引导，特别是成文的程序法不仅具有控制行政行为的职能，还可以对行政主体的自由裁量行为进行监督，有利于行政主体依法行使职权，有效克服实体法的缺陷，补充实体法本身的不足，以其特有的功能补充实体法控制权力的不足，达到权力与权利的平衡、效率与自由的协调、形式合理性与实体合理性的结合。水行政执法过程中，执法主体和执法人员的素质参差不齐，如任由其追求执法目标而不对其执法过程加以监督和制约，必定会带来诸多负面影响。通过正当法律程序的指导和约束，可以对水政监察机关的执法行为进行必要的监督。

由竖转体系稳定性计算分析结果可知，在竖转过程中竖转架和钢拱塔不会发生第一类和第二类安全失稳.但考虑计算模型与现场的施工过程存在的差异性，以及钢拱塔作为永久设施的重要性，为了保证竖转过程和正常使用过程中独塔斜拉桥的绝对安全，提出了两种增强钢拱塔稳定性的措施[9-10].

图6　稳定索安装示意图

钢拱塔安装了稳定索后，塔脚的位移及应力都有所减小.经过计算，钢拱塔在80°工况时，塔脚的应力约为9.24 MPa(见图7)，和不设稳定索时的应力30.5 MPa相比减小了69.7%，横向位移仅为1.2×10-5m.这些都说明稳定索的安装很大程度地改善了拱脚处的应力和位移状况，提高了竖转体系的稳定性.

鞑靼部起初入据河套，首先，是出于在蒙古部落内部发展强大的需要。也先土木之战的胜利，不仅暴露了明朝边防的空虚，也使鞑靼部感到严重威胁，为了抑制瓦剌势力的继续扩张，鞑靼部企图占领位于东西通道上的河套地区。其次，是游牧经济自身的缺陷决定了鞑靼部在农产品、日常生活用品等方面不能自给自足，所以鞑靼部迫切需要与内地进行经济联系。河套地区是联系蒙古和中原的纽带，自然就成为天然的交换通道。

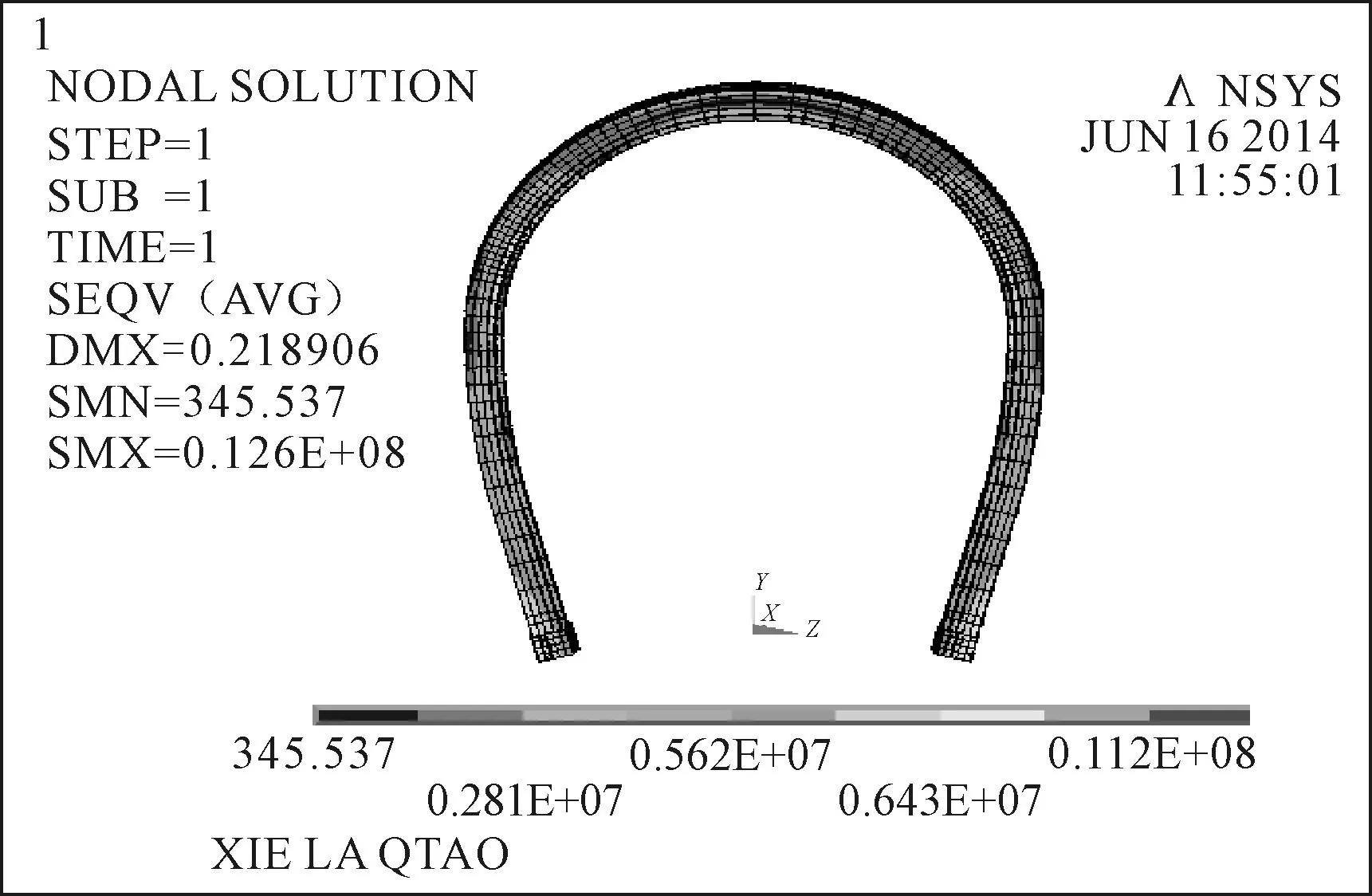
图7　钢拱塔应力云图

4.2安装平衡索

若说有什么缺憾之处，我总感倘全书备有人物、剧名等索引，估计更便于读者查检事实，可更能体现图志本身已经具有的工具书之价值。

钢拱塔在双向提升装置的牵引下，缓缓离开胚架，在竖转的过程中，为了提高钢拱塔的稳定性，在钢塔上设置了平衡索，安装位置见图8.平衡索能保证竖转过程中索力始终保持在安全索力以上，避免夹片式锚具松锚，保证竖转体系的稳定性.若不设置平衡索，钢拱塔在竖转过程中重心将不断前移，特别是小倾斜角度钢拱塔的竖转体系重心很可能超出竖转铰垂面，造成整体向牵引方向倾覆.

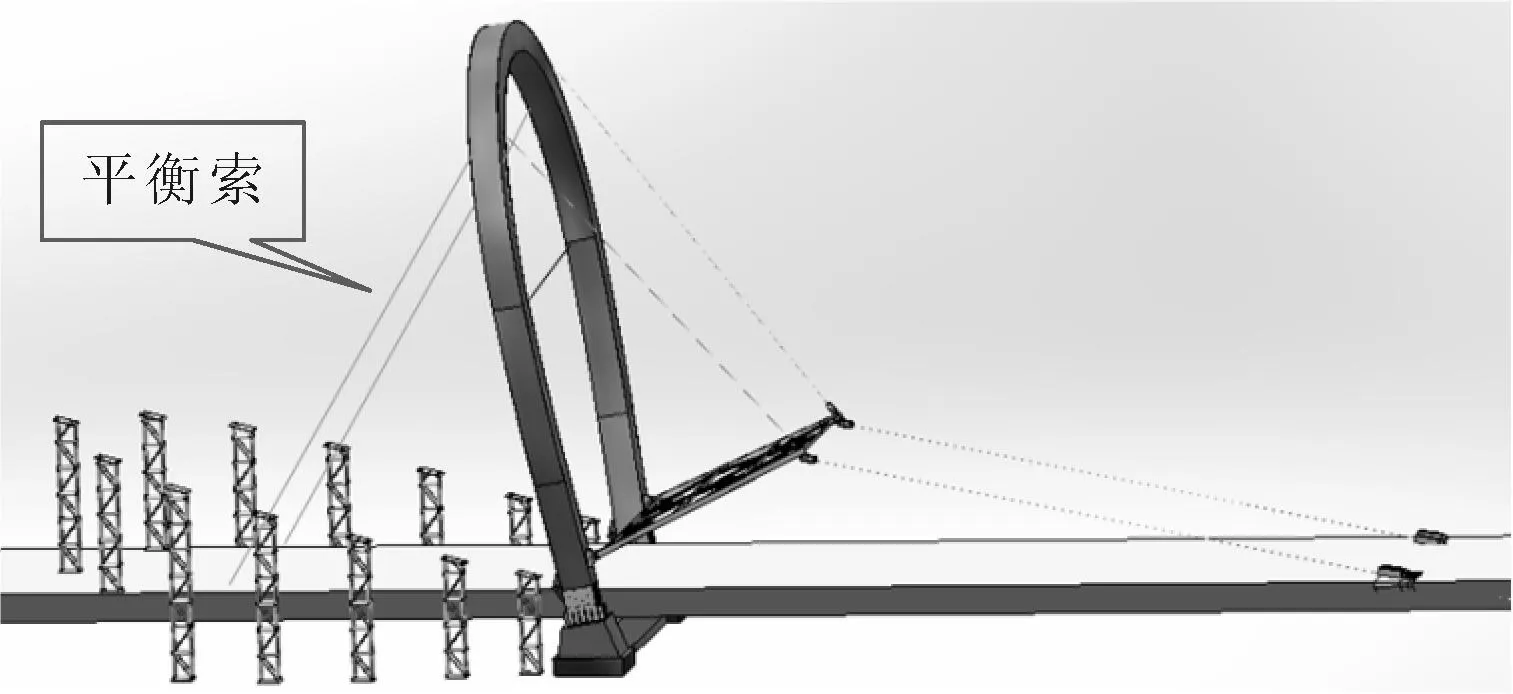
图8　平衡索安装示意图

平衡索为两束钢绞线，每束9根钢筋，钢绞线的一段与主梁连接，另一端锚固在钢钢拱塔上，通过索力控制钢拱塔的位移.平衡索从钢钢拱塔竖转到70°工况后开始工作，到达完成工况(80°工况)时单根拉锁索力为40 kN，以保证整体结构受力平衡，防止钢拱塔整体倾倒.平衡索在斜拉索安装完毕后卸载.

中本聪提出一种点到点的现金系统[1]，并在2009年公开了源代码。通过社区的推进，人们开始尝试使用比特币进行支付，第一个例子就是使用一万个比特币购买一个披萨。比特币源于社区，并自带粉丝，社区内成员自我铸币、自我消费。继比特币之后，出现了如莱特币[2]、点点币[3]、名字币[4]等以各种名目发行的密码货币，因其总量固定，所以粉丝越多其汇率越高。

5结论

1) 对该双向牵引竖转体系的稳定性分析结果表明：竖转过程中体系稳定性可以得到保障，竖转架及钢拱塔所受到的荷载均小于其线性屈曲临界荷载及塑性极限荷载，两个关键结构的稳定性也可以得到保障.

2) 在竖转过程中，稳定索的设置能显著改善拱铰处的位移和应力状况，增强了钢拱塔的稳定性.

3) 平衡索的采用能避免整个竖转体系的倾覆，保证了竖转过程中该双向牵引竖转体系的整体稳定性.

参 考 文 献

[1]丁美.结构稳定性分析中ANSYS的应用[J].低温建筑技术,2003(6):42-44.

[2]王新敏.ANSYS工程结构数值分析[M].北京:人民交通出版社,2007.

[3]林立孚.基于ANSYS的钢结构平面外稳定分析[J].工业建筑,2011(4):388-390,364.

[4]李晓亮.某大跨钢管混凝土系杆拱桥稳定性计算分析[J].山东交通科技,2014(2):44-47.

[5]鞠彦忠,刘维春.基于ANSYS的独塔斜拉桥非线性分析[J].东北电力大学学报,2007,27(1):11-14.

[6]王玉山,闫琴,金瑾.基于有限元法的桥梁结构稳定性分析[J].石河子大学学报：自然科学版，2012,28(1):106-108.

[7]梁弢.钢结构稳定性问题探析[J].建筑技术,2012(1):19-23.

[8]潘秋生.钢结构设计中稳定性分析[J].中国建筑金属结构,2013(7):20-21.

[9]张宝宏.基于有限元的斜拉桥索塔竖转结构件设计[J].城市建筑,2014(3):25-30.

[10]谢文兵,荆升国,王涛，等.U型钢支架结构稳定性及其控制技术[J].岩石力学与工程学报,2010,29(2):3743-3748.

Research on Stability and Control Measures of

Single Tower Cable-stayed Bridge

WANG XiangyangXIA XiaoyongHAN Lili

(SchoolofTransprotation,WuhanUniversityofTechnology,Wuhan430063,China)

Abstract：Based on the single tower cable-stayed bridge on Gaoxin 2nd Road in Wuhan, a vertical rotation system incorporating vertical turret and steel arch pylon was proposed. The model of the whole bridge was built by the FEM program ANSYS and the stability of the single tower cable-stayed bridge was analyzed. The vertical rotation system won’t lose it’s balance in the construction process according to the calculation results. Finally, two preventative measures were proposed to ensure the stability of the vertical rotation systeml and the complete function of the single tower cable-stayed bridge.

Key words：single tower cable-stayed bridge; vertical rotation construction; stability analisis; steel arch pylon; vertical turret

收稿日期：2015-11-16

doi:10.3963/j.issn.2095-3844.2016.01.004

中图法分类号：TU311.41