关于函数定义域求法的探析报告
2016-03-04吕骥
吕 骥
(鄂南高级中学,湖北 咸宁 437100)
关于函数定义域求法的探析报告
吕 骥
(鄂南高级中学,湖北 咸宁 437100)
毫无疑问,函数是中学阶段最重要的一个知识点,也是高中数学学习的一道分水岭。函数的基础知识在现实生活、社会、经济及其他学科中有着广泛的应用;函数概念及其反映出的数学思想方法已广泛渗透到数学的各个领域,是进一步学习数学的重要基础。而函数的定义域又是函数中重要的“三要素”之一,如何准确地求出函数的定义域,自然就成为了重中之重。在学习过程中,老师们应当讲解清楚定义域的常见求法。
函数;定义域;常见方法
函数在高考和各类数学竞赛中都有广泛的应用,属于必考内容,既是重点内容又是难点内容。想要攻克这一重难点,必须探析清楚定义域的常见求法。以下分具体函数和抽象函数两大类型来介绍定义域求法。
一、具体函数求定义域
已知函数的解析式求定义域,一般有以下几种情况:
(1)分式中的分母不为零;
(2)偶次方根下的数(或式)大于或等于零;
(3)零指数幂的底数不等于零;
(4)指数式的底数大于零且不等于一;
(5)对数式的底数大于零且不等于一,真数大于零。
当以上几个方面有两个或两个以上同时出现时,先分别求出满足每一个条件的自变量的范围,再取他们的交集,就得到函数的定义域。
例1:求下列函数的定义域:
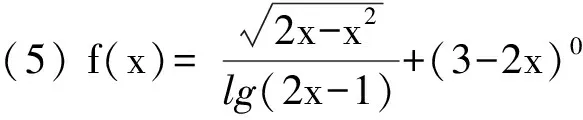

∴x<-2且x≠-4,故其定义域为{x<-2且x≠-4}。
∴x≤-3且x≠-11或x>5,故其定义域为 {x|x≤-3且x≠-11}∪{x|x>5}
∴-4 (1) 求A; (2) 若B⊆A,求实数a的取值范围。 ∴A=(-∞,-1)∪[1,+∞)。 (2) 由(x-a-1)(2a-x)>0,得 (x-a-1)(x-2a)<0。 ∵a<1,∴a+1>2a,∴B=(2a,a+1), a≤-2.又a<1, 解得1 综上所述,使得函数的定义域为R的a的取值范围是[1,9]。 小结:会求函数的定义域是正确求解一切函数问题的基础,求解时要注意找全找准限制条件,并正确找到公共部分,且最后定义域一定要写成集合或区间的形式。 抽象函数是指没有明确给出具体解析式的函数,解决其有关问题是具有一定难度的,特别是求其定义域时,会令许多学生感到迷惑。 下面结合实例介绍抽象函数定义域问题的几种题型及求法: 1.已知f(x)的定义域,求f[g(x)]的定义域。 求解思路:若f(x)的定义域为m≤x≤n,则在f[g(x)]中,m≤g(x)≤n,解得x的取值范围构成的集合,即为f[g(x)]的定义域。 例4:已知函数f(x)的定义域为[-2,3],求函数f(x2-1)的定义域。 解:令-2≤x2-1≤3,得-1≤x2≤4,解得-2≤x≤2, 故函数的定义域是[-2,2]。 2.已知f[g(x)]的定义域,求f(x)的定义域。 求解思路:若f[g(x)]的定义域为a≤x≤b,则由a≤x≤b确定的g(x)的范围构成的集合,即为f(x)的定义域。 例5:已知函数f(x2-2x+3)的定义域为[-1,3],求函数f(x)的定义域。 解:由-1≤x≤3,得2≤x2-2x+3≤6, 令u=x2-2x+3,则f(x2-2x+3)=f(u),2≤u≤6, 故f(x)的定义域为[2,6]。 3.已知f[g(x)]的定义域,求f[h(x)]的定义域。 求解思路:可先由f[g(x)]定义域求得f(x)的定义域,再由f(x)的定义域求得f[h(x)]的定义域。 例6:已知f(2x-1)的定义域为[1,2],求 f(x2)的定义域。 解:由1≤x≤2,得1≤2x-1≤3, 故φ(x)的定义域为[-4,0]。 小结:求抽象函数的定义域最主要的还是要掌握函数定义域的实质,其操作要领总结起来就是两点:一是什么是函数的定义域(即自变量x取值范围的集合,函数f(x)的自变量是x,函数f[g(x)]的自变量也是x;二是同一个对应法则下代数式的取值范围一致(即f[g(x)]中的g(x)和 f[h(x)]中的h(x)取值范围一致。 2095-4654(2016)12-0014-03 2016-11-06 G634 A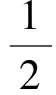
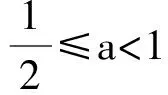

二、抽象函数求定义域