培养初中生用数学概念解决问题的几点感悟

戴荣臻

摘要：学生从小学进入初中的学习以后，数学概念特别多，每一单元都以学习数学概念为开头，再以这些数学概念为基础，进行运用和拓展。学生对概念的掌握只是一知半解，不能很好的理解和运用，严重影响了学生的学习成绩。

关键词：初中；数学概念；数学方法；数学能力

中图分类号：G633.6文献标识码：B文章编号：1672-1578（2016）02-0161-01

刚入学的初一年新生对于数学概念的学习基本上停留在"识记、背诵"阶段，虽然老师们在上每一节课时，都会特别注意一些细节的讲解，但过了一段时间后，学生不是忘记就是把一些概念混淆，更不用说对这些概念进行熟练运用了。学生从小学进入初中的学习以后，数学概念特别多，每一单元都以学习数学概念为开头，再以这些数学概念为基础，进行运用和拓展。作为教师，我们在平时教学中，注意细节的讲解，让学生养成良好解题习惯，而学生对概念的掌握只是一知半解，不能很好的理解和运用，严重影响了学生的学习成绩。如何转变学生从小学时养成的概念思维惯性？怎样促进学生学好初中数学概念？这就摆在初中数学教师需要思考的问题：

我在多年的教学中，感悟到学生学习数学的困难。作为教师需要有广泛的知识面，不仅要对初中数学知识了解透彻，而且甚至是学科外的东西也要了解一些，这样可以不断延伸学生的知识面，做好一些细节。我在教学过程中，特别注重概念细节的讲解和描述。要让学生想要学好数学，归根到底必须先学好数学概念。但传统教学教师重解题轻概念，造成数学解题与概念的脱节，这就加剧学生学习新概念的难度。新课程标准下教师如何教好数学，使学生学起概念更容易，概念教学显得特别重要。下面是我在平时的教学中的一些做法，供大家指正。

1.教师在上课时把抽象的数学概念引用生活化例子讲解

我经常把概念与生活联系在一起间接转移知识，让学生产生共鸣提高学习的感知度。当再有涉及到这些概念时学生就会联想到实际的生活，过目不忘。例如学习数轴概念，它的定义是："规定了原点、正方向、单位长度的直线叫做数轴。"这个概念教师不好讲解，学生也不好掌握。但是把数轴和温度计联系在一起就很好的帮助学生理解和记忆了：温度计上的零度就相当数轴上的原点；温度表上每一刻度就相当数轴上的每一个单位长度；而高于零度的方向就是正方向。这样数学概念学习与生活联系在一起就不再那么抽象，反而觉得更形象、生动了，纯粹的概念课变得不再那么枯燥无味了。

2.合理的对知识进行延伸，从多种的角度理解同一概念

初中数学中有一些概念可以从不同的角度进行理解，提高学生的思维能力。比如学习相反数，它的定义："是只有符号不同的两个数叫做相反数。"我们可以多种分析；1、从定义角度：求5的相反数，只要在5的前面加负号。2、从数轴角度理解：什么样的两点表示数是互为相反数的。把5与-5分别描在数轴上很直观的得到"相反数位于原点两侧，与原点的距离相等"。3、除此之外相加为零的两个数也可以称为互为相反数。教学中从不同角度的教数学概念可深化学生对数学概念的理解，提高学生分散思维的习惯养成。

3.注意数学概念中细微之处，讲解清楚部分条件的限制

务必注意概念中给出的条件的限制，忽视了某一条件，就会出现理解上的偏差，这种理解上的偏差不容易一下发觉。例如平行线的定义："在同一平面内不相交的两条直线叫做平行线。"如果忽略了"在同一平面内"的条件限制，那么不相交的两条直线就不一定会平行线。如图：与AB不相交的直线有A1B1、C1D1、CD、DD1、CC1 A1D1、B1C1，其中只有A1B1、C1D1、CD与AB在同一平面内且不相交（符合条件限制），因此得出结论它们互相平行。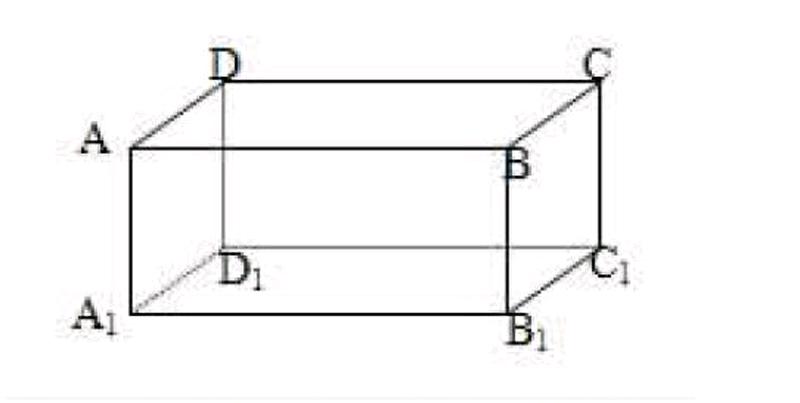

4.教师采用合适教法，讲清概念表达的本质属性

学生在大部分的数学考试中，都有对数学概念的本质没有弄明白，遇到题目就乱答一通，造成最基础知识直接或间接的失分。学生数学基础没有掌握，解题做不来也就对数学学习失去兴趣，最终连信心也丢失，成绩也就一落千丈。因此教师应重视基础的数学概念的教学。比如：求3的相反数是__； -3的倒数是__等。这些数学题是非常基础和简单的对概念知识的直接考查；另外学生在学习几何角度中会把35。的余角答成145。，他们把余角和补角的两个概念间接弄糊涂了。学生常混淆概念、张冠李戴造成不必要的失分。我常把直接或间接相近的概念拿来比较，要求学生分清概念本质。也就减轻了学生学习难度，又加深印象，再通过练习巩固记忆。

5.教师创设学习情景，把概念分解成几个小概念，降低概念学习的难度

初一的数学概念常以"定义式"出现，它的特点是严谨、抽象。老师对于这样的概念应对其进分解成几个小点进行教授，引导学生正确的记忆和理解。如：学习一元一次方程的概念"只含有一个未知数，并且所含未知数的最高次数是1次的 整式方程"时，我把这个概念分成"只含有一个未知数"、" 所含未知数的最高次数是1次"、" 整式方程"这样几个部分，完成对各个部分逐一讲解的基础上再强调这一概念的整体性，丢一不可。