发射点垂线偏差对导弹惯性制导精度的影响分析*

夏巍巍,牟建华,王 旭

(火箭军装备研究院,北京 100094)

发射点垂线偏差对导弹惯性制导精度的影响分析*

夏巍巍,牟建华,王 旭

(火箭军装备研究院,北京 100094)

为分析并修正发射点垂线偏差对导弹惯性制导精度的影响,建立了完整的惯性制导误差传递模型,通过基于标准弹道参数的误差仿真,得出不同射程、射向条件下垂线偏差引起的惯性制导误差特性,其中,视加速度投影误差是产生制导误差的主要因素,引力加速度计算误差和自瞄准误差的影响也不可忽略。利用该误差传递模型对垂线偏差影响进行计算和修正,可有效提高导弹惯性制导精度。

垂线偏差;惯性制导;误差传递模型

0 引言

纯惯性制导自主性强,不易受干扰,是导弹武器必保的制导手段,精确制导武器也需要由惯性制导为末制导提供必要的交班条件。初始对准误差是影响导弹惯性制导精度的重要因素,除惯性器件自身测量误差外,发射点垂线偏差也会引起初始对准误差[1]。在已知垂线偏差的前提下,通过误差影响分析由其引起的惯性制导误差并修正,能有效提高惯性制导精度。垂线偏差影响伴随整个飞行过程,难以获得解析解,已有分析多采用简化处理,例如引力计算误差只考虑发射点位置偏差影响等[2],会引入一定计算误差,且制导误差多以传统惯性弹道为分析对象,只计算关机点误差对落点影响[2-3],对全程制导导弹尤其是新型非弹道式导弹并不适用。

为解决上述问题,在垂线偏差作用机理研究基础上,建立了完整的误差传递模型,采用基于标准弹道参数的误差积分方法进行仿真计算,以全程制导状态不同射程、不同射向的弹道为对象,分析了垂线偏差引起的惯性制导误差特性及主要误差项,为制导误差修正提供了依据和手段。

1 垂线偏差基本概念

垂线偏差定义为大地水准面垂线与参考椭球体法线之间的夹角,是由于地球表面形状不规则、地球内部质量分布不均匀等地理自然因素引起的。

图1中,以地面观测点O为中心作任意半径的辅助球,OP表示地轴方向,OZ、OZ1分别表示过O点的垂线和法线,u表示垂线偏差,ξ、η分别为垂线偏差在子午圈和卯酉圈上的分量。

B、L分别为天文纬度、经度;φ、λ分别为大地纬度、经度,两者之间的关系如下[3]:

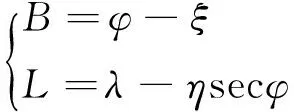
(1)

拉普拉斯方程描述了天文方位角α与大地方位角A的近似归算关系[4]:

A=α-ηtanφ

(2)

图1 垂线偏差示意图

2 发射点垂线偏差影响机理分析

2.1 垂线偏差对初始对准的影响

导弹起飞前,弹上惯性器件通过敏感重力加速度获得调平参数Δφz、Δφy,即初始调平以垂线为基准。对瞄准环节,若采用弹上自瞄准,惯性器件通过敏感重力加速度和地球自转角速度解算瞄准方位角,该方位角为天文方位角,与大地方位角存在的偏差如(2)式所示;若采用地面间接瞄准,由于经纬仪调平及水平转动均以垂线为基准,垂线偏差对方位角瞄准结果产生的影响如下[5]:

(3)

式中:θ为经纬仪瞄准弹上棱镜的仰角;A0表示发射方位角。根据上式,θ=0时,垂线偏差对方位角瞄准的影响很小,即水平瞄准时,方位角瞄准受垂线偏差的影响可忽略。

综上,通过初始对准建立的惯性导航坐标系以发射点垂线为基准,而弹道设计采用惯性坐标系则以法线为基准,两者间的差异由垂线偏差引起。法线坐标系与垂线坐标系之间的方向余弦阵如下:

CF=M2[-A0]·M1[η]·M3[-ξ]·

M2[A0+η·tanφ0]

(4)

式中:A0为发射方位角;φ0为发射点大地纬度;M1[α]、M2[α]、M3[α]分别为绕x轴、y轴、z轴旋转α角度的方向余弦阵。

忽略二阶小量,得到简化的法线坐标系到垂线坐标系的转换矩阵如下:

(5)

2.2 初始对准误差对惯性导航解算的影响

导航解算采用的垂线坐标系与弹道设计采用的法线坐标系间存在偏差,将引起制导误差。导航解算模块在初始速度基础上,对加速度进行积分运算,计算导弹惯性系速度、位置,其中,加速度包含视加速度和引力加速度两项,以上过程均会因为坐标系存在偏差而引入计算误差。

2.2.1 视加速度投影误差

(6)

式中ΔCF=(CF-I3×3)为投影误差矩阵。

2.2.2 引力加速度计算误差

引力加速度根据导弹当前位置进行计算[6],计算模型此处不再赘述。位置解算误差会引起g值计算误差,g值误差又反过来产生导航解算误差。为简化分析,忽略带谐项,则引力矢量对载体位置的偏导数阵为:

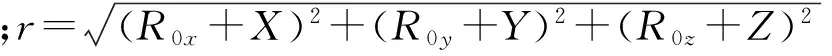
(7)

2.2.3 初始速度计算误差

点火时刻惯性系初始速度为发射点牵连速度:

V0e=εe×R0

其中,εe、R0分别为地球自转角速度和发射点地心矢在发射惯性系的投影矢量,由于导航计算时采用垂线坐标系,相对法线坐标系初始速度计算误差为:

ΔV0e=ΔCFV0e

(8)

2.2.4 位置解算误差

初始速度计算误差、视加速度投影误差和引力加速度计算误差共同引起位置解算误差,以Y方向为例,误差微分方程组为:

(9)

式中：初值为ΔY0=0,ΔVy0=ΔV0ey。

图2 1 600 km弹道误差仿真结果

3 发射点垂线偏差影响仿真分析

3.1 试验条件设置

全程制导是实现精确制导的必要条件,也是导弹武器发展的重要方向,为此选取2条典型弹道,根据上文误差传递模型开展全程制导状态下发射点垂线偏差的误差影响仿真。试验条件设置如下:

1)发射点纬度B0=40°,经度L0=110°,高程H0=1 000 m;

2)发射方位角从0°～360°按45°间隔取8组;

3)典型弹道射程分别约为1 600 km、10 000 km;

4)垂线偏差按ξ=10″和η=10″分别进行仿真;

5)自瞄准和地面水平瞄准状态分别仿真。

3.2 仿真结果分析

1 600 km弹道下惯性制导误差随发射方位角的变化曲线如图2所示,其中蓝色曲线为纵向偏差,红色曲线为横向偏差;10 000 km弹道下误差随发射方位角的变化曲线如图3所示。

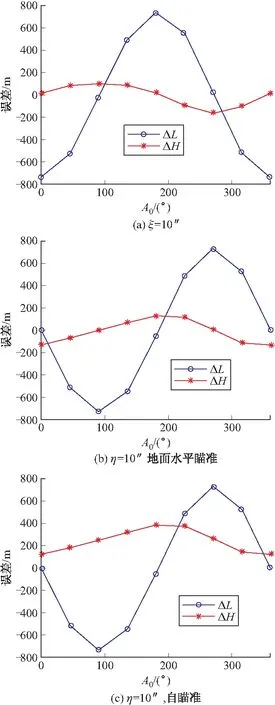
图3 10 000 km弹道误差仿真结果

根据上述仿真结果,垂线偏差引起的惯性制导误差有如下规律:

1)随着发射方位角从0°增大到360°,垂线偏差引起的纵、横向制导误差围绕零值附近呈正弦波动,周期为360°。这主要是由于:垂线偏差引起的导航坐标系误差为发射方位角正、余弦函数的线性组合(如式(5)),因此,随着发射方位角从0°增大到360°,由此引起的制导误差呈正弦波动。

2)子午分量与卯酉分量随发射方位角变化产生的偏差波动幅值相当,相位相差90°。这主要是由于:子午分量和卯酉分量引起的惯性导航坐标系误差均与发射方位角的正、余弦函数呈线性关系,形式相同,并存在90°相差。

3)小射程弹道下,纵、横向制导误差波动幅值相当,两者均随射程增大而增大,但横向误差波动幅值随射程增大的幅度相对纵向较小,即大射程弹道下,纵向误差幅值显著高于横向。这主要是由于:根据式(6),垂线偏差作用下,惯性系Y向位置解算误差主要由X向视加速度投影误差累加引起,而X向、Z向位置解算误差主要由惯性系Y向视加速度投影误差累加引起,前者相对后者较大,即由垂线偏差引起的惯性系Y向误差大于X向和Z向,小射程弹道下,惯性系Y向误差投影至纵向的分量较小,对纵向影响不显著;而大射程弹道下,惯性系Y向误差投影至纵向的分量逐渐增大,直至射程约10 000 km时,惯性系Y向误差几乎全部投影至纵向,从而引起较大的纵向误差。

4)存在卯酉分量时,自瞄准方式下的横向误差相对地面水平瞄准状态存在一定偏移量,即正弦波动的中值由零值上移。这主要是由于:自瞄准方式下,瞄准方位角为天文方位角,相对弹道设计所采用的大地方位角存在偏差,由此带来的导航坐标系误差引起附加横向误差。

3.3 引力加速度计算误差影响分析

根据仿真计算结果,在垂线偏差作用下,引力加速度计算误差对制导误差的影响如表1所示,表中以1 600 km和10 000 km弹道为例,分别列出ξ=10″和η=10″条件下的制导误差影响,ΔL、ΔH、Δh分别表示纵向、横向和高程方向。图4为10 000 km弹道制导误差影响随发射方位角的变化曲线。

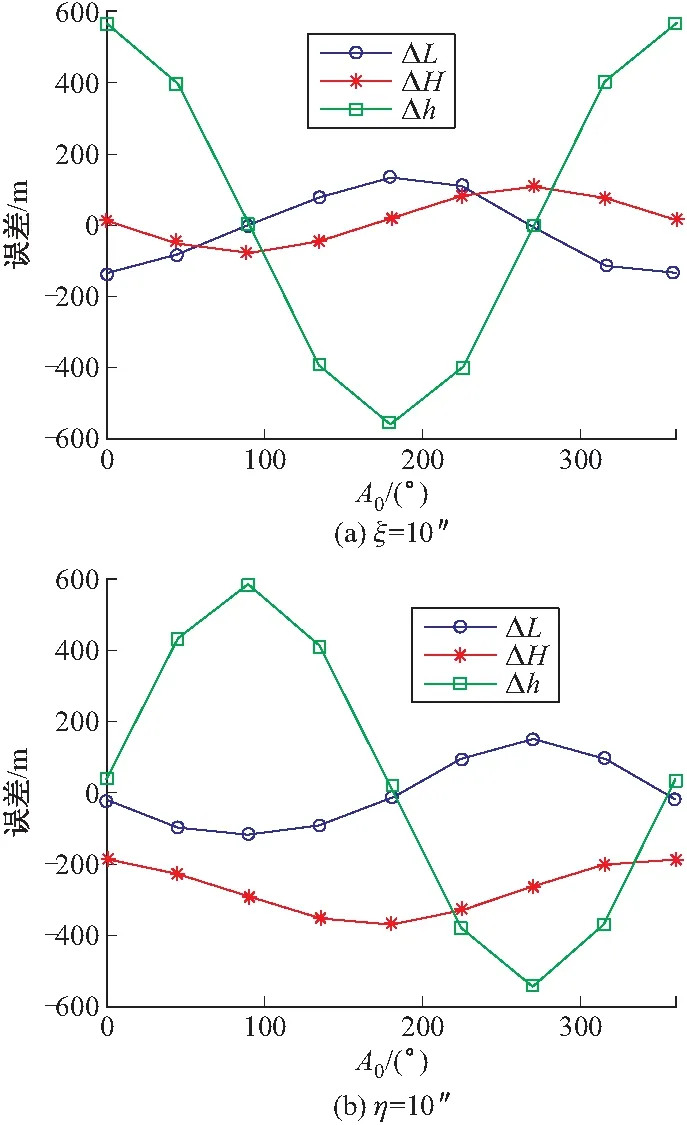
图4 引力加速度计算误差对制导误差的影响

可以看出,

1)引力计算误差对制导误差的影响随发射方位角变化呈正弦波动,这主要是由于垂线偏差引起的惯性坐标系误差为发射方位角正、余弦函数的线性组合,在该初始误差作用下,引力计算误差引起的导航误差也随发射方位角呈正弦波动;

2)引力计算误差对高程方向的影响比对纵、横向的影响大,随着射程增大,该现象更为显著,这主要是由于高度通道存在正反馈,导航时间越长,由引力计算误差引起的高度解算误差越大。

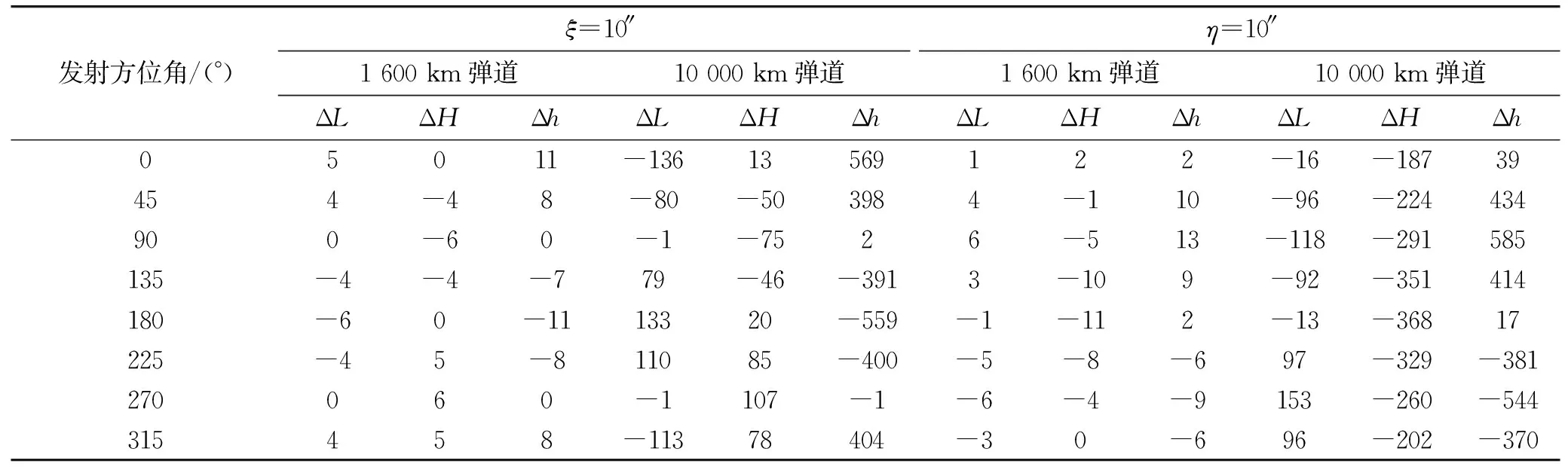
表1 引力加速度计算误差对制导误差的影响 m

3.4 垂线偏差作用下自瞄准影响分析

根据仿真计算结果,相对地面水平瞄准,垂线偏差卯酉分量通过影响自瞄准精度而引起的制导误差如表2所示:

表2 卯酉分量(η=10″)通过自瞄准误差引起的制导误差 m

可以看出,在卯酉分量作用下,采用自瞄准主要对横向误差产生影响,在特定射程弹道下,不同发射方位角下的影响量值较为接近,因具体弹道形式不同而存在小幅波动。

4 结论

在垂线偏差影响机理研究的基础上,通过误差仿真对发射点垂线偏差在不同射程、射向弹道条件下引起的惯性制导误差进行了分析,主要结论如下:

1)随着发射方位角从0°增大到360°,垂线偏差引起的纵、横向制导误差呈正弦波动;

2)垂线偏差引起的纵、横向偏差随射程增大而增大,且纵向偏差随射程增大的幅度大于横向;

3)垂线偏差引起的惯性制导误差中,视加速度投影误差占主要因素,此外,引力加速度计算误差和自瞄准误差的影响也不可忽略,其中,引力加速度计算误差对高程误差影响较大,存在卯酉偏差时自瞄准会对横向偏差产生影响。

利用文中提供的惯性制导误差模型对垂线偏差影响进行射前计算及弹道修正,可有效提高导弹惯性制导精度。

[1] WANG Wei. The determination of the deflection of vertical using inertial surveying system [J]. Journal of National University of Defense Technology, 1995, 17(3): 126-130.

[2] 杨辉耀. 大地测量误差对导弹精度的影响与修正 [J]. 飞行力学, 1998, 16(1): 43-49.

[3] 马清华, 赵久奋, 王明海. 发射点垂线偏差修正研究 [J]. 弹箭与制导学报, 2004, 24(4): 396-398.

[4] 孔祥元, 郭际明, 刘宗泉. 大地测量学基础 [M]. 武汉：武汉大学出版社, 2005: 82-84.

[5] 郑应强, 康宁民, 冯伟利, 等. 垂线偏差对惯性制导初始方位角的影响 [J]. 中国惯性技术学报, 2010, 18(2): 170-174.

[6] 郑伟. 地球物理摄动因素对远程弹道导弹命中精度的影响分析及补偿方法研究 [D]. 长沙: 国防科学技术大学, 2006.

Influence Analysis of Launch Point Vertical Deflection on Missile Inertial Guidance Precision

XIA Weiwei,MU Jianhua,WANG Xu

(The Rocket Force Equipment Academy, Beijing 100094, China)

To analyze and correct the influence of launch point vertical deflection on missile inertial guidance precision, a complete error-transfer model of missile inertia guidance was established. Inertia guidance error characteristic of different range and direction was analyzed by error simulation based on standard trajectory parameter. Projection error of apparent acceleration is the main factor of guidance error, while the calculation error of gravitational acceleration and self-aiming error cannot be neglected either. Based on this error-transfer model, vertical deflection influence can be calculated and corrected, which has contributed to improve missile inertial guidance precision.

vertical deflection; inertial guidance; error transfer model

2015-09-23

夏巍巍(1982-),女,河南汝南人,助理研究员,硕士,研究方向:弹道仿真、导航制导与控制。

TJ013.2

A