高帽变换和toggle算子组合的图像增强优化算法*

张 扬,郑 宾,刘 珊

(1 中北大学电子测试技术国家重点实验室,太原 030051;2 北华航天工业学院,河北廊坊 065000)

高帽变换和toggle算子组合的图像增强优化算法*

张 扬1,郑 宾1,刘 珊2

(1 中北大学电子测试技术国家重点实验室,太原 030051;2 北华航天工业学院,河北廊坊 065000)

针对灰度图像对比度较低而难以识别目标区域的问题,对形态学中传统的高帽变换算子和toggle算子进行组合,提出了基于高帽变换和toggle算子组合的图像增强优化算法。该算法利用高帽变换算子增大原始图像灰度值的动态范围,同时利用toggle算子锐化图像,使图像清晰。实验结果表明,该组合算子相对单个算子来说,对灰度图像的对比度增强效果更好,目标识别效果更佳。

高帽变换;toggle算子;对比度;图像增强;目标识别

0 引言

图像增强是图像处理的一种重要技术,已被广泛应用在生物医学工程、指纹识别、天文图像和红外图像处理等不同方面[1]。图像增强的主要思想是通过增大图像中明亮区域和暗淡区域的对比度,以获得更好的视觉效果。很多图像受成像传感器、背景辐射和成像环境操作的影响,具有较低的对比度。为了提取图像关键信息进行目标识别,需要对杂波背景里的目标区域进行增强。

为了增强不同应用的图像,人们提出了多种图像增强算法,包括小波理论[2],对比度拉伸算法[3],模糊逻辑算法[4]和数学形态学算法[5-7]。控制对比度拉伸可以达到图像增强的结果,但是部分图像区域可能被抑制,将影响部分结果图像的效果;小波算法可以提取不同尺度上有用的图像特征,但一些图像细节得不到很好的增强效果,并且结果图像不是很清晰;基于模糊逻辑的算法将图像视为不确定的集合,以此来定量和增强重要的图像区域,尽管图像对比度能够有所增强,但结果会产生一些模糊痕迹。基于数学形态学的算法,是实现对比度增强的一类重要算子。基于高帽变换[8]的对比度算子是其中之一,可以有效地抑制杂波背景,提取图像的特征,增大原始图像灰度值的动态范围,使图像增强,但是增强后的结果不是很清晰,toggle对比度算子[9]是形态学的另一种对比度增强算子,能够锐化图像,使图像清晰,但不能增大原始图像灰度值的动态范围。为了使目标图像增强效果更好,更容易进行目标识别,将上述两种算子进行优势互补,文中提出了基于高帽变换和toggle算子组合的图像增强优化算法。

1 传统高帽变换和toggle算子

腐蚀和膨胀是数学形态学的基本运算,将两种运算组合,可形成开运算和闭运算[9]。先腐蚀后膨胀的过程称为开运算,先膨胀后腐蚀的过程称为闭运算。腐蚀可以使目标缩小,消除小于结构元素的噪声点;膨胀可以使目标增大,添补目标中的空洞;开运算和闭运算分别通过消除图像上的细小噪声和填补图像的细小空洞来平滑物体边界。灰度数学形态学是文中研究的基础,其基本运算如式(1)～式(4)所示:

1)灰度膨胀

(a,b)∈Df,(u,v)∈DB}

(1)

2)灰度腐蚀

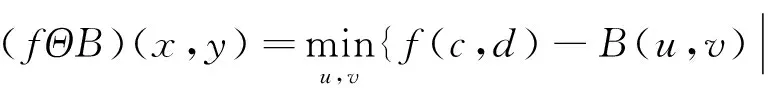
(c,d)∈Df,(u,v)∈DB}

(2)

3)灰度开运算

(f∘B)(x,y)=(fΘB)⨁B

(3)

4)灰度闭运算

(f·B)(x,y)=(f⨁B)ΘB

(4)

式中:f为原始图像;B为结构元素;Df和DB分别是f和B的定义域;a=x-u;b=y-v;c=x+u;d=y+v。

1.1 高帽变换对比度算子

运用开运算和闭运算的算子,Meyer提出了高帽变换算子,高帽变换可以分为白高帽变换和黑高帽变换,分别表示为WTH和BTH,定义如式(5)和式(6)所示。

白高帽变换:

WTH(x,y)=f(x,y)-(f∘B)(x,y)

(5)

黑高帽变换:

BTH(x,y)=(f·B)(x,y)-f(x,y)

(6)

WTH用来提取明亮图像区域,BTH用来提取暗淡图像区域。高帽变换对比度算子(oTH)的基本思想是在原始图像中加上提取的明亮图像区域并且减去提取的暗淡图像区域,如式(7)所示。

oTH(x,y)=f(x,y)+WTH(x,y)-BTH(x,y)

(7)

在oTH中,加上WTH的结果,明亮图像区域的灰度值变大,减去BTH的结果,暗淡图像区域的灰度值变小,从而增强了明亮和暗淡图像区域间的对比度。因为原始图像的灰度值发生了改变,其动态范围被拉大,对图像区域增强十分有效。

1.2toggle对比度算子

toggle对比度算法(oTC)可以用于图像锐化和分割,其定义如式(8)所示。

(8)

图像每个像素的灰度值经过膨胀或腐蚀,进行选择输出。因此,在oTC里,图像边缘区域部分灰度值将会被膨胀或腐蚀结果的灰度值替换,使图像锐化和清晰达到增强的目的。toggle对比度算子是一种遵循不同规则的对膨胀图像、腐蚀图像或原始图像灰度值的选择性输出,因此原始图像灰度值的动态范围将不会改变。

2 组合对比度优化算子

高帽变换对比度算子通过增大明亮和暗淡图像区域间的对比度提高了原始图像对比度,能平滑部分图像区域但并不能使增强后的图像清晰;toggle对比度算子锐化图像区域使图像清晰,但因原始图像灰度值的动态范围没有改变,原始图像不能得到有效增强。有效的对比度算子应既能增强图像对比度又能使增强后的图像清晰,将基于高帽变换的对比度算子和toggle对比度算子相结合即可达到此目的。基于这个思想,基于上述两个对比度算子,可以实现两种不同类型算子的组合。

2.1 顺序对比度算子

将基于高帽变换的对比度算子与toggle对比度算子进行顺序交替,即先在原始图像上运行基于高帽变换的对比度算子,然后在结果图像上运行toggle对比度算子,或进行相反操作。这种顺序交替的操作称为顺序对比度算子,分别表示为so1和so2,如式(9)和式(10)所示。

so1=oTH(oTC(f(x,y)))

(9)

so2=oTC(oTH(f(x,y)))

(10)

so1和so2的定义表明,原始图像首先被基于高帽变换的对比度算子(或toggle对比度算子)增强,再被toggle对比度算子(或基于高帽变换的对比度算子)增强。所以,图像可以得到双重增强。

2.2 联合对比度算子

将基于高帽变换的对比度算子的结果输入到toggle对比度算子中作为一个算子。oTC是一个遵循不同规则的3幅不同图像(f,f⨁B和fΘB)的选择性输出结果,然后,将f替换为oTH,基于高帽变换的对比度算子即可被输入到toggle对比度算子中,实现组合。

在oTC中将f替换成oTH至少有两种方式,其组合对比度算子可分别表示为co1和co2,如式(11)和式(12)所示。

(11)

(12)

co1和co2的定义表明,oTH的结果遵循不同的规则与oTC进行组合,组合结果可遵循不同的规则进行选择性输出,可在不同应用中达到不同的增强效果。

3 实验结果及分析

3.1 实验结果

形态学算子的一个非常重要的参量就是结构元素的形状。一般来说,结构元素的形状有矩形、正方形、菱形和圆形等。因为圆形没有尖角并且能抑制一些棱角可能产生的痕迹,因此被广泛用在不同的应用中,文中选用圆形结构元素,结构元素的大小尺寸也是一个重要参量。结构元素根据不同的应用来定义大小尺寸,一般在区间[1,10]里。文中在所有的操作里选用的结构元素大小尺寸为2,以便作对比。综上,文中所用结构元素是半径为2的圆形结构元素。

为了显示组合对比度算子的效力,选用Walkbridge图像,如图1所示。应用不同的方法进行增强,在Matlab7.1上运行[10],实验结果如图2所示。

图1 Walkbridge原始图像

从图中可以看出,oTH算子增强了图像对比度,oTC算子锐化了原始图像,co1算子得到与oTC处理后相似的效果。so1、so2和co2算子不仅增强了原始图像的对比度,也有效的锐化了图像,使目标更容易识别,在所有形态学对比度算子处理的图像结果中视觉效果最好。

3.2 实验结果分析

文中采用一个空间频率量度(F)[9]对实验中的算法作一个定量比较。F是一个量化图像质量的有效测量参数,它基于图像清晰度定义,图像视觉效果越好,细节越清晰,F值越大。令f为一幅M×N图像,利用空间行频率(F1)和空间列频率(F2)的均方根来计算F,定义式如式(13)至式(15)所示。

图2 Walkbridge图像增强结果

(13)

(14)

(15)

计算oTH、oTC、co1、co2、so1和so2的F值,对应于每个算子处理结果的F值如表1所示。从表1可以看出,所有算子均可增强图像。co1的F值接近于oTH和oTC的F值,表明co1可以增强图像对比度并且性能与oTH和oTC相似,这是因为仅仅很少数量的像素在co1的定义里满足“其他”条件规则,即仅仅很少数量的像素被oTH里同样像素的灰度值替换。如果更多像素在一些情况下满足“其他”条件规则,co1的结果会更好;so1、so2和co2的F值比oTH和oTC的值大很多,表明组合对比度算子很好的结合了oTH和oTC的优势,图像增强效果比原始形态学对比度算子更好。

表1 利用F值的不同算子的定量比较

4 结论

文中提出了基于高帽变换和toggle算子组合的图像增强优化算法,该方法将传统的高帽变换对比度算子和toggle对比度算子组合,利用不同的算子组合结果,选取相同的结构元素,对同一幅Walkbridge图像进行增强处理。实验结果表明,同单个算子处理结果相比,组合算子对灰度图像的对比度增强效果更好。通过计算不同算子的空间频率量度,对几种算子的增强效果进行定量比较得知,组合算子对图像增强的性能更好。因此,可根据需要,将其应用在不同的图像目标增强与识别中,应用前景广泛。

[1] 李艳梅. 图像增强的相关技术及应用研究 [D]. 成都: 电子科技大学, 2013.

[2] 尹士畅, 喻松林. 基于小波变换和直方图均衡的红外图像增强 [J]. 激光与红外, 2013, 43(2): 225-228.

[3] 徐卫昌, 黄威, 李永峰, 等. 低通滤波与灰度值调整在图像增强中的应用 [J]. 激光与红外, 2012, 42(4): 458-462.

[4] 阮秋琦. 数字图像处理学 [M]. 北京: 电子工业出版, 2001: 15-38.

[5] 袁俊. 数学形态学理论及其在图像处理中的应用 [D]. 武汉: 武汉理工大学, 2007.

[6] HARALICK R M,STERNBERG S R,ZHUANG X. Image analysis using mathematical morphology [J]. IEEE Transactions on Pattern Analysis and Machine Intellignce, 1987,9(4): 532-550.

[7] SERRA J. Mathematical morphology and its applications to image processing [M].[S.l.]Kluwer Academic Publishers, 1994:78-91.

[8] 朱士虎. 形态学高帽变换与低帽变换功能扩展及应用 [J]. 计算机工程与应用, 2011, 47(34): 190-192.

[9] 崔屹. 图像处理及分析——数学形态学方法及应用 [M]. 北京: 科学出版社, 2009: 128-136.

[10] CHAPMAN Stephen J. MATLAB编程 [M]. 北京: 科学出版社出版, 2007: 76-92.

Optimization Algorithm for Enhancement of Image Based on Combination with Top-hat Transformation and Toggle Operator

ZHANG Yang1,ZHENG Bin1,LIU Shan2

(1 National Key Laboratory for Electronic Measurement Technology, North University of China, Taiyuan 030051, China; 2 North China Institute of Aerospace Engineering, Hebei Langfang 065000, China)

Since it is difficult to enhance target region of gray image with low contrast, traditional morphological top-hat transformation and the toggle operator were combined, and an optimization algorithm for enhancement of image based on the combination was put forward. The algorithm uses top hat transformation operator to increase dynamic range of the gray value in original image and uses the toggle operator to sharpen the image, which can make the image clear at the same time. The experimental results show that the combination operator has better effect on contrast enhancement of gray scale images compared with single operator, and the effect of the target recognition is better.

top-hat transformation; toggle operator; contrast; image enhancement; object recognition

2015-10-13

张扬(1989-),男,山西平遥人,硕士研究生,研究方向:动态测试。

TP751.1

A