基于迭代误差补偿的发射点坐标精确求解方法

温永禄，马 骏，黄 蓓，李 强，许 诺

（中国运载火箭技术研究院，北京 100071）

0 引言

随着现代化战争的动态化和复杂化发展，军事信息系统将是提升现代化战争下指挥员指挥能力、发挥武器装备作战效能的重要抓手［1-2］，而军事信息系统经常涉及到发射点精确计算问题，该问题属于CGCS2000 坐标系下的大地主题解算。对于小射程的导弹武器，目前通常采用6°带高斯平面坐标，并采用高斯平面坐标计算距离和方向等参数，但是由于高斯平面坐标存在分带处理，对于大射程的导弹武器，在计算距离和方向等参数时，与真实情况存在较大偏差［3-4］。因此，为适应新形势下的作战和装备发展需求，通常采用大地主题解算算法，解决不同射程下的发射点坐标计算问题。

目前针对椭球模型下的大地主题解算问题，还没有可用于直接解算椭球面三角形的解析求解方法。国内外众多学者一直关注该问题并提出了多种解算方法，分别适用于短距离、中距离和任何距离。对于短距离（小于120 km），比较典型是史赖伯（O. Schreiber）公式和高斯平均引数公式［5-6］，该公式是在勒让德（Legendre）的基础上，利用大地线终点在起始子午圈上的垂足，用以解算大地主题。此后，高斯（Gauss）提出把勒让德技术改化成大地线起点和终点的平均纬度和平均方位角为引数的幂级数，这样勒让德级数式中所有的偶次幂都消失了，可使项数减少，从而大大加速了级数的收敛，形成高斯平均引数公式，最终达到大地主题问题解算的目的，但是其解算精度与距离有关，距离越长，收敛越慢，因此，只适用于较短的距离。对于中距离（小于400 km）大地主题解算，常用的是巴乌曼投影公式，巴乌曼采用椭球面对球面的等距离投影方法求解大地主题［7］。针对中长距离解算问题，贝塞尔（Bessel）提出将椭球面上的参数按一定条件投影到辅助球面上，然后由边长和经差投影公式求出辅助球面参数表示的大地要素［8］，实现从球面到椭球面上的相应转换。贝塞尔大地投影的方法，解算的距离相比高斯平均引数法要远得多，依据白塞尔的这种解法，派生出许许多多的公式［9-10］，有的是逐渐趋近的解法，有的是直接解法，还有的是其简化公式，例如导航使用的大地线长近似计算公式，白塞尔公式的直接解法——陈俊勇公式，保持纬度不变的大地投影——张志新公式［11］。韦森特（T.Vincenty）以贝塞尔公式为基础，推导出嵌套系数公式［12-14］。1985年，张学廉以该公式为基础，采用嵌层约化的方法对幂级数及系数进行改化，推导出3 个嵌套系数和两个迭代改正数，进而求解距离和经差改正项，该方法统称为韦森特公式，也称为嵌套系数法，可适用于任何距离的大地主题解算，而且计算量小。韦森特公式能够适用于线长从数厘米到近20 000 km的大地问题解算，大地线长的精度为毫米级，大地方位角的精度为0.000 1 s，并且我国于2008 年颁布了GJB6304-2008《2000 中国大地测量系统》，推广了韦森特公式的使用。

针对军事信息系统火力筹划运用需求，为实现对目标的精确打击，通常需要预先根据导弹武器的射程、发射点方位角（射向）、目标点坐标，精确计算发射点坐标，供载机航线规划和作战规划使用，该问题是一种非典型的大地主题解算问题，目前尚未形成统一的计算方法解决该问题。因此，针对该问题，本文在大地主题正解的基础上，提出一种基于迭代误差补偿的非典型大地主题解算方法，根据已知的发射点方位角、目标点坐标和射程，初步计算目标点方位角，采用射向迭代法，再调用大地主题正解模型求得新的发射点方位角，求取两次发射点方位角之间的偏差，利用偏差对目标点方位角进行补偿修正，进一步减小发射点方位角误差，直至计算得到的发射点方位角与已知的发射点方位角误差小于预设的极小值，从而解决发射点坐标精确计算问题，该方法计算适用射程范围广、精度高、计算量小，能够满足军事信息系统工程化运用需求。

1 典型大地主题解算方法

假设发射点大地经纬度为B1，L1，发射点至目标点的大地方位角（射向）为A12和射程S，目标点大地经纬度为B2，L2，目标点至发射点的大地方位角为A21，各角度及距离示意图如图1 所示。

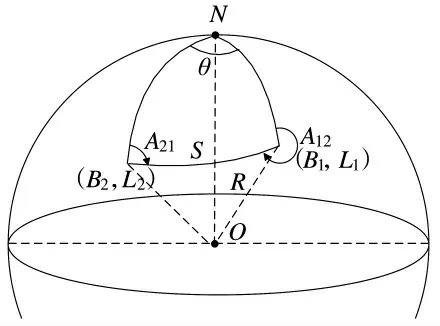
图1 大地问题解算示意图

CGCS2000 地球椭球参数表如表1 所示：

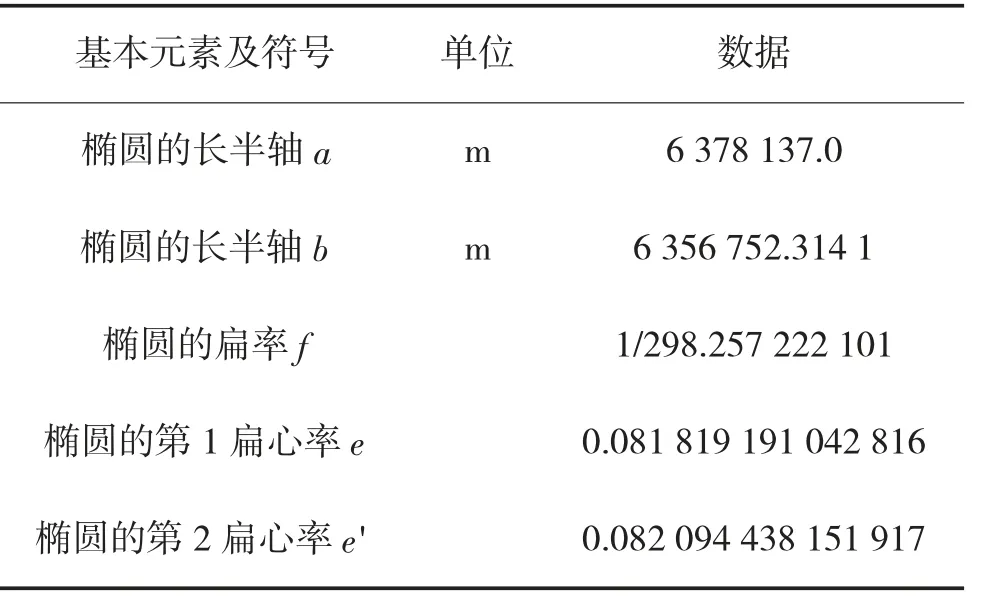
表1 CGCS2000 地球椭球参数表

1.1 大地主题正解

大地主题正解问题是根据发射点的大地经纬度B1、L1和发射点至目标点的大地方位角A12和射程S，推求目标点大地经纬度B2、L2和目标点至发射点的大地方位角A21。GJB6304-2008《2000 中国大地测量系统》［12］给出的标准算法计算步骤如下：

发射点（B1、L1）的地心纬度u1正切三角函数：

从赤道到发射点连线在球上的角距σ1的正切三角函数：

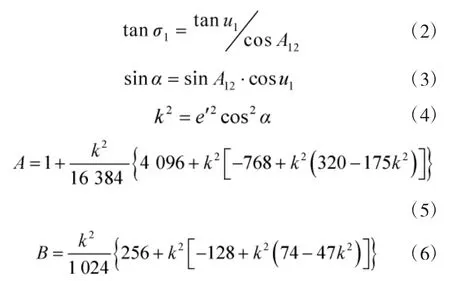
从发射点到目标点连线在球上的角距σ 近似值：

依次迭代计算如下3 个公式：

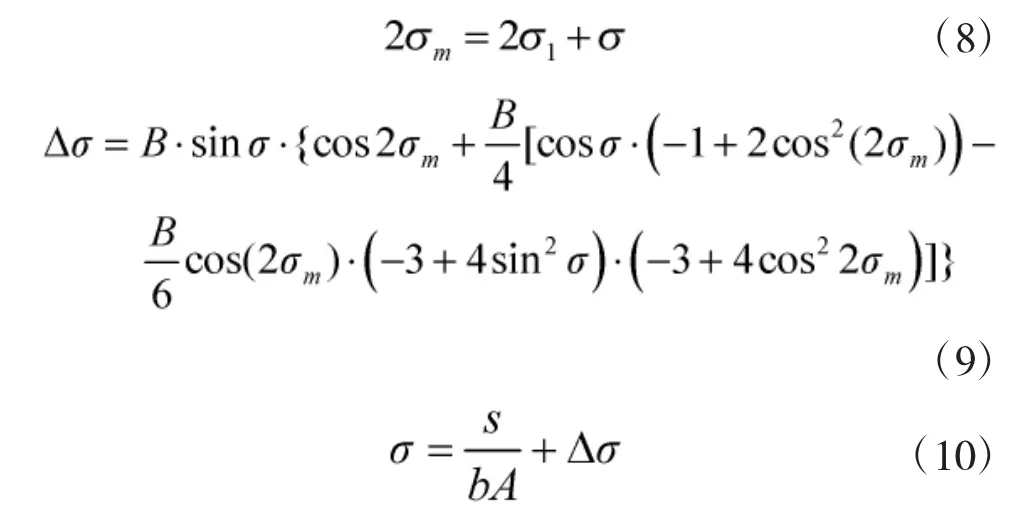
直至σ 无显著变化之后（变化值小于MIN=10-10），计算：

目标点（B2、L2）的大地纬度B2正切三角函数：

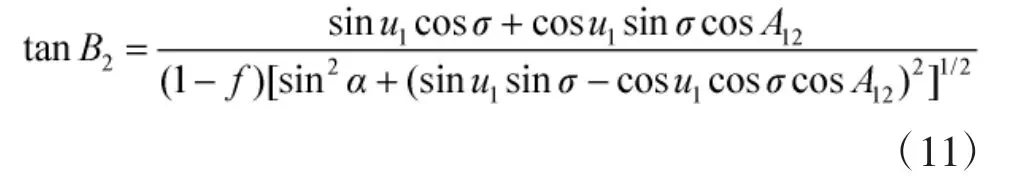
发射点（B1、L1）和目标点（B2、L2）在辅助球上的经差正切三角函数：

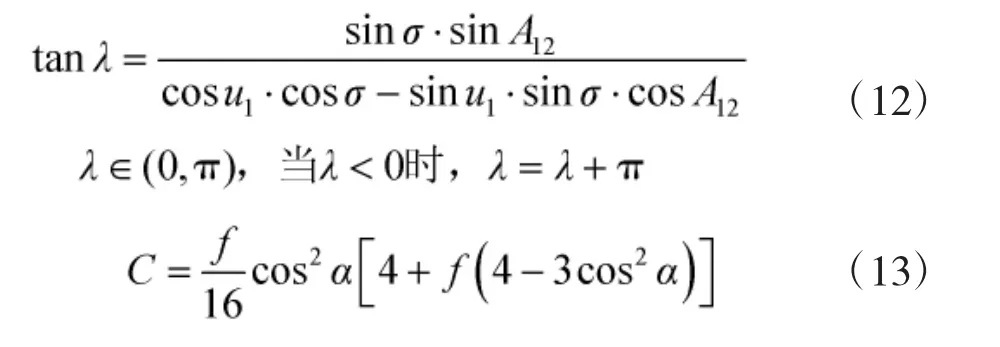
发射点（B1、L1）和目标点（B2、L2）的经差ΔL

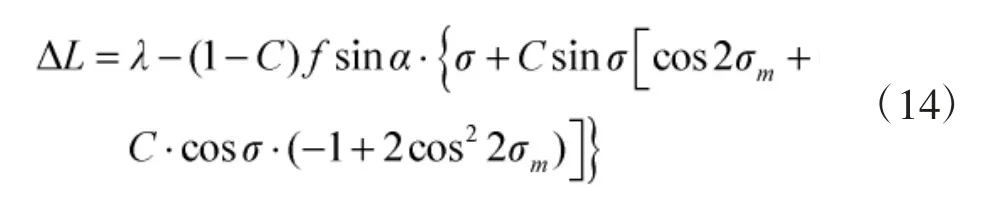
目标点（B2、L2）的大地经度L2：

目标点（B2、L2）的大地方位角A21的正切三角函数：

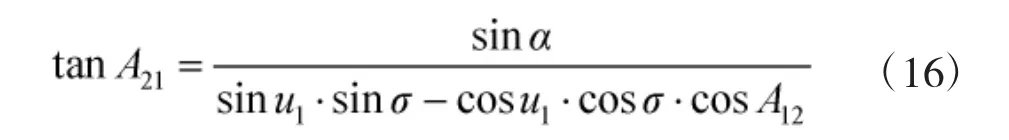
该模型同样适用于已知目标点坐标、射程、目标点方位角，计算发射点坐标和发射点方位角的情况。

1.2 大地主题反解

大地主题反解问题是根据已知发射点、目标点的大地经纬度B1、L1、B2、L2，求两点之间射程S 和正反大地方位角A12、A21。GJB6304-2008《2000 中国大地测量系统》［5］给出的标准算法如下。

发射点（B1、L1）的地心纬度正切三角函数：

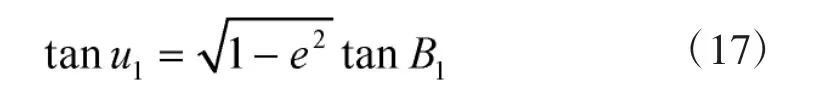
目标点（B2、L2）的地心纬度正切三角函数：

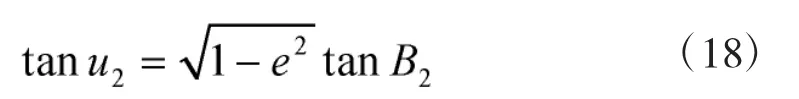
依次迭代计算如下公式：

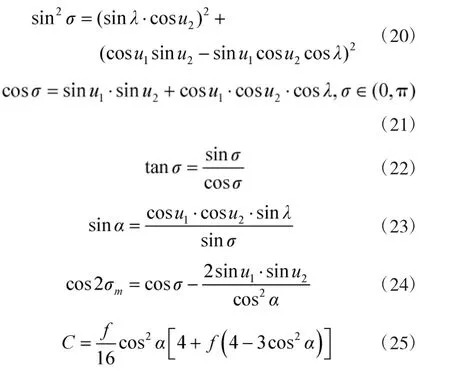
发射点（B1、L1）和目标点（B2、L2）之间的射程：

发射点（B1、L1）的大地方位角A12的正切三角函数：

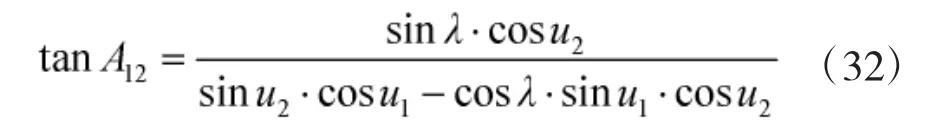
目标点（B2、L2）的大地方位角A21的正切三角函数：

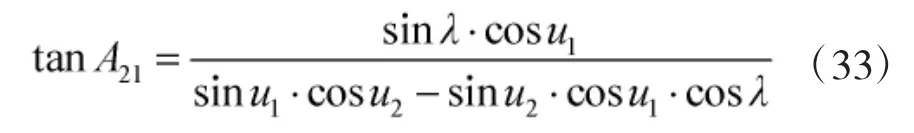
当两点接近对趾时，反解公式可能无解。（对趾问题是指两点的直线连线穿过参考椭球球心的情况，主要指射程在20 000 000 m 左右，具体解决方法见文献［8］）。

2 基于迭代误差补偿的非典型大地主题解算方法

根据射程、射向（发射点方位角）和目标点坐标，计算发射点坐标、目标点方位角，该问题是非典型的大地正解问题［13］，已知目标点大地经纬度B2、L2和发射点至目标点的大地方位角A12和射程S，推求发射点大地经纬度B1、L1和目标点至发射点的大地方位角A21。具体求解流程如图2 所示。

1）首先，根据A12，估算得出初步的A'21；

2）根据初步计算的A'21、目标点大地纬经度B2、L2、射程S，调用大地主题正算模型，计算发射点大地方位角A'12；

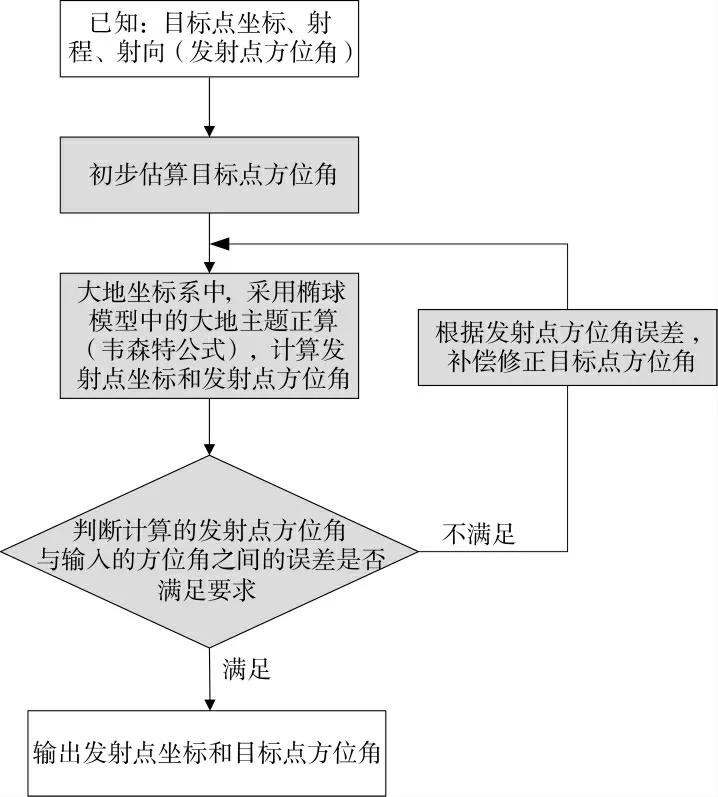
图2 非典型的大地正解计算流程

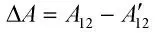
4）采用迭代法进行求解，循环计算以下步骤，直至ΔA 小于给定的极小误差值；

②根据更新后的A'21、输入的目标点大地纬经度B2、L2和射程S，调用大地主题正算模型，计算发射点大地方位角A'12；

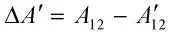
④判断ΔA' 是否小于给定的极小误差值（MIN=10-10）；如果满足，则退出迭代；如果迭代次数超过最大迭代次数（TIMES=400），则逐步放大迭代误差要求（乘以10 倍，MIN=10-9，10-8，…，10-3）直至迭代误差不大于10-3；

5）根据最终计算得到的A'21、输入的目标点大地纬经度B2、L2和射程S，调用大地主题正算［14］，得出发射点纬经度B1、L1。

3 算例分析

为验证本文提出方法的正确性和适用性，在Win7 i7-6700 3.4 GHz Matlab 2012b 的环境下进行仿真测试，极小值取值10-10，计算时间约0.1 s。为验证算法的正确性，选用国军标GJB6304-2008《2000中国大地测量系统》中的算例进行计算对比；为验证算法的适用性，在20 000 000 m 的射程范围内，随机在全球范围内生成发射点和目标点坐标，形成计算样例，对计算结果的适用性进行分析。

3.1 与GJB 中的算例对比

根据GJB6304-2008《CGCS2000 中国大地测量系统》中提供的解算算例，以目标点经度L2、目标点纬度B2、射程S、发射点方位角A12为输入计算发射点经度L1、发射点纬度B1和目标点方位角A21，以标准中的算例结果为参考对计算结果进行对比分析。

通过与标准算例中的结果进行对比，计算偏差如图3 所示，计算得到的发射点坐标纬度最大偏差为0.000 333''，经度最大偏差为0.000 121''，发射方位角偏差最大为0.000 196''，满足发射点坐标的计算精度要求。

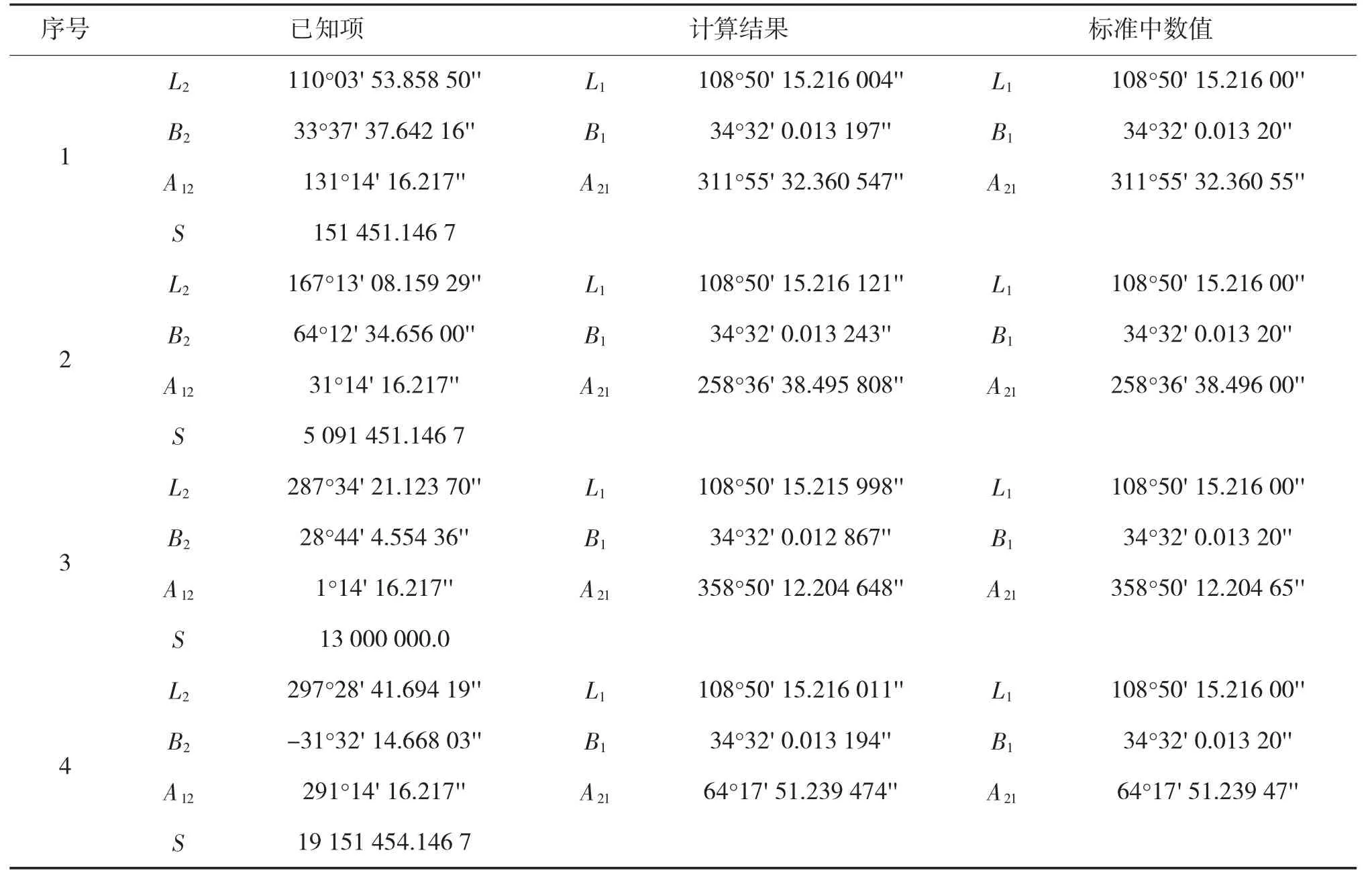
表2 仿真计算结果

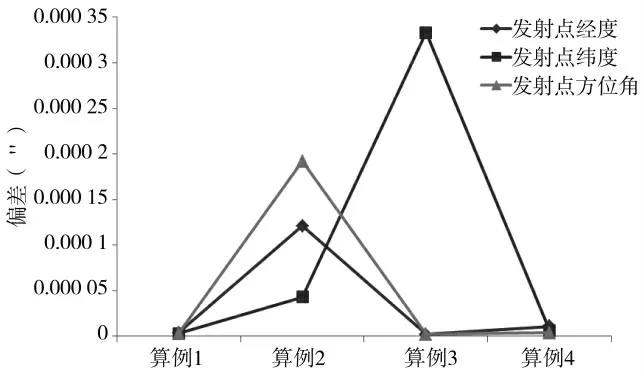
图3 与标准算例的计算偏差

3.2 随机测试算例

在目标点坐标纬度范围［-90，90］°，经度范围［0，360）°，射程［0，20 000 000］m，射向［0，360）°范围内，随机生成测试样例，测试次数设置为5 000 次，对结果进行统计与分析。首先，根据目标点坐标、射程、射向（发射点方位角），采用非典型的大地主题正解模型计算发射点坐标、目标点方位角［15］；然后再根据得到的发射点坐标，结合目标点坐标，采用国军标中的大地主题反解公式计算射程、发射点和目标点方位角，并与已知射程、发射点方位角和非典型大地主题解算计算得到的发射点坐标进行对比，分析计算误差如下页图4～图6 所示。

根据仿真计算结果可看出，在设定的数据取值范围内，随机生成的5 000 个测试样例中，射程计算偏差绝对值最大为6.08×10-3m，偏差量级为10-3m；发射点方位角偏差绝对值最大为7.23×10-7°m，偏差量级为10-7°（10-4''），目标点方位角偏差绝对值最大为7.78×10-7°，偏差量级为10-7°（10-4''），计算精度能够满足发射点精确计算要求，而且算法具有很好的鲁棒性。

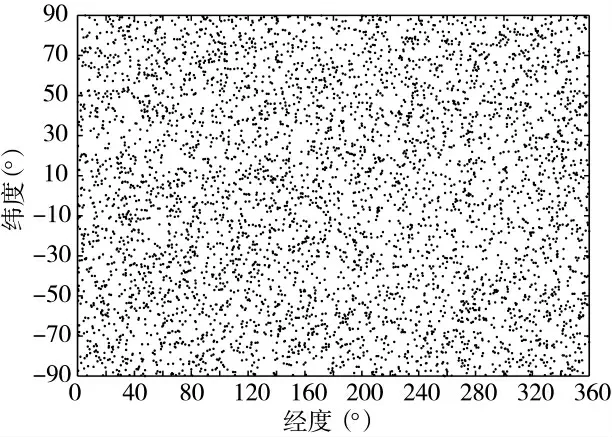
图4 目标点坐标分布

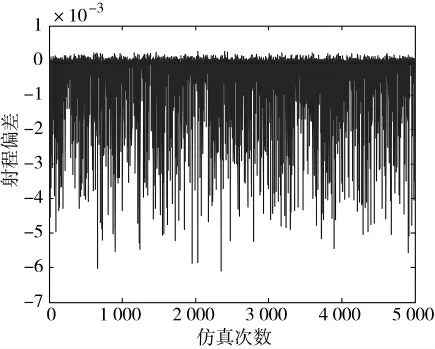
图5 射程偏差

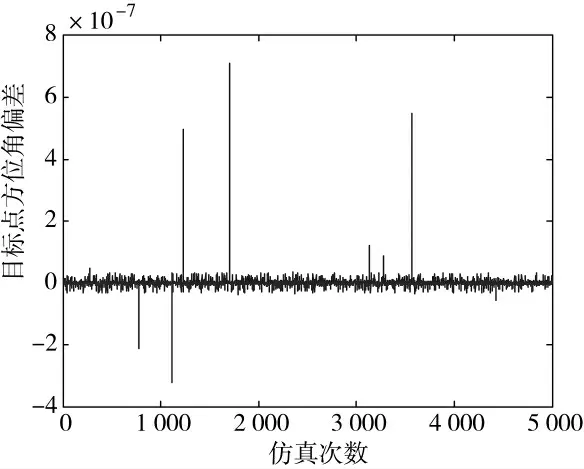
图6 目标点方位角偏差

图7 发射点方位角偏差

4 结论

本文通过分析发射点精确计算特点，在大地主题正算（韦森特公式）、大地主题反算求解方法的基础上，提出一种基于迭代误差补偿的非典型大地主题正解方法，采用国军标GJB6304-2008 中的算例和随机测试样例，对算法的适用性和精确性进行验证，通过仿真结果进行分析可知，本文提出的方法适用于20 000 km 内任意两点的发射点精确计算，方法简单实用，能够满足军事指挥控制信息系统的发射点坐标精确计算要求。