基于跑道的视觉导航信息分析*

张红良,郭鹏宇

(国防科学技术大学航天科学与工程学院,长沙 410073)

基于跑道的视觉导航信息分析*

张红良,郭鹏宇

(国防科学技术大学航天科学与工程学院,长沙 410073)

基于跑道的视觉导航广泛用于无人机自主着陆等场合。文中从信息的角度,分析了视觉导航中跑道边缘线、地平线和跑道横向控制线提供的姿态和位置导航信息,推导并证明了两个基本结论:已知宽度的跑道边缘线可以提供两个姿态和两个位置信息;地平线和跑道横向控制线可以完善姿态和位置信息。文中的研究对于进行基于跑道的视觉导航算法设计、精度分析和组合导航可观性分析等具有理论价值。

视觉导航;跑道;地平线;无人机着陆

0 引言

无人机近年来成为研究和应用的热点,自主着陆是无人机自动化智能化的关键环节,基于视觉的无人机自主着陆技术受到持续的关注和研究[1-9]。基于视觉的着陆技术利用机载视觉传感器对跑道或着陆区域成像,通过图像分析,利用视觉导航或组合导航计算无人机的位置、姿态等参数。从用于着陆导航的视觉信息看,基于视觉的着陆技术主要分为两类:一类视觉导航信息来源于在着陆场或跑道布设合作特征点或特征结构[1,3,5-8];另一类视觉导航信息直接来源于跑道边缘或地平线[2,4,10-11]。基于跑道边缘或地平线等信息的视觉着陆方法无需人工特定设置合作特征物,具有更广泛的适用性,可用于一般跑道,并可扩展至在高速公路上的着陆场合或基于跑道灯光的着陆场合[12]。

不同于已有文献基于跑道的无人机着陆视觉导航具体算法[2,4,10-11]的设计,文中立足于分析无人机着陆中跑道(地平线)能够提供的视觉信息,从理论上推导跑道方向、跑道宽度、地平线和跑道横向控制线对视觉系统姿态和位置的约束关系。文中的研究对于进行基于跑道的视觉导航算法设计、精度分析和导航可观性分析等具有理论价值。

1 坐标系描述

为便于后面的描述,不失一般性,首先对相关坐标系进行定义和描述。

定义跑道坐标系(W系)为:原点OW在跑道中心线上,XW轴沿跑道方向,YW轴沿高度方向(向上为正),ZW轴指向跑道侧向(以右手直角坐标系确定正向)。

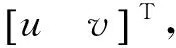
(1)

其中:Fx、Fy为视觉传感器的等效焦距;Cx、Cy为视觉传感器的像面主点,对于已标定视觉传感器,Fx、Fy、Cx和Cy都为已知量。

(2)

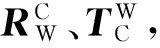
2 跑道边缘线视觉导航信息分析

对视觉导航来说,跑道的信息主要体现在跑道方向和跑道宽度上,下面从这两个方面分别分析,最后总结相关结论。

2.1 跑道方向提供的姿态导航信息

如图1所示,两条平行的跑道边缘线L1和L2成像为l1和l2,根据小孔成像原理,视觉系统斜视跑道时l1和l2不平行,延长线相交于点Vp,点Vp称为边缘线图像的消隐点(vanishing point)。由于物理空间的跑道边缘线平行,消隐点对应跑道坐标系XW轴方向无穷远处点的像,光心到消隐点的连线矢量与跑道坐标系XW轴方向平行:OCVp∥XW,其单位矢量在跑道坐标系内可表示为:

(3)

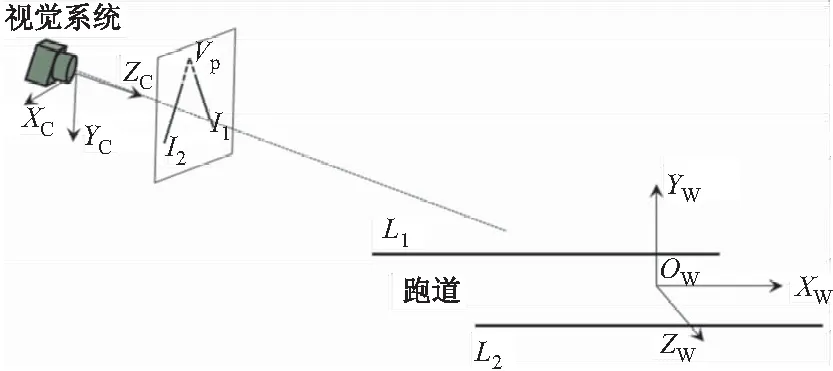
图1 视觉系统对跑道成像示意图

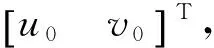
(4)

(5)

原理上,根据式(3)～式(5)可以确定俯仰角和偏航角姿态导航信息(绕跑道坐标系XW轴旋转角即滚转角无法确定)。

不失一般性,下面利用一种姿态角定义方法给出证明。在无人机着陆导航过程中,滚转角、俯仰角和偏航角一般定义为无人机体相对于跑道坐标系的姿态。为方便推导,假设视觉系统的光轴(ZC轴)与无人机机头方向一致,YC轴垂直机身向上,XC在机身平面内指向左侧,则跑道坐标系按Y-Z-X-Y(2-3-1-2)顺序依次旋转偏航角φ、俯仰角θ、滚转角γ和90°后与视觉测量坐标系重合,视觉测量系统姿态矩阵为:

(6)

将式(3)、式(4)和式(6)代入式(5),整理可得:

(7)

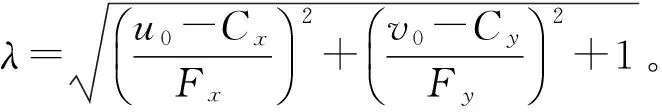
若滚转角γ已知,则可以求解出俯仰角θ和偏航角φ。即根据跑道方向(跑道边缘图像消隐点)可以确定俯仰角和偏航角信息。

因此,跑道方向可以提供俯仰角和偏航角姿态导航信息。

2.2 跑道宽度提供的位置导航信息

如图2所示,设跑道宽度为2Z0,则两条跑道边缘线方程在跑道坐标系(W系)内的表示为

(8)

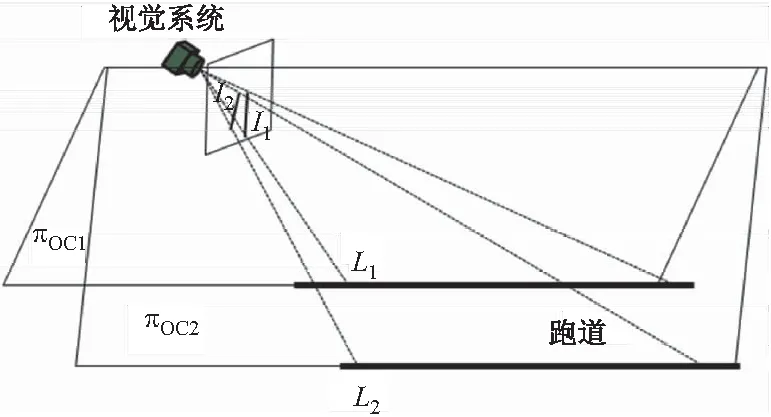
图2 跑道边缘线对位置的约束

则视觉系统光心和跑道边缘线L1和L2组成的平面方程在跑道坐标系内满足方程:

(9)

式中m1、n1、m2、n2为待定参数。式(9)也可写成:

(10)

式中i=1,2,且s1=n1Z0,s2=-n2Z0。

根据跑道边缘线在图像上的直线(图2中l1和l2)可拟合出其直线方程分别为:

li:v=kiu+di,i=1,2

(11)

式中ki、di(i=1,2)为拟合参数。

设视觉系统光心与图像直线l1和l2组成平面(等同于光心和跑道边缘线L1和L2组成的平面)在视觉测量坐标系(C系)中满足方程(像机光心为视觉测量坐标系原点,因此方程无常数项):

i=1,2

(12)

式中ai、bi、ci(i=1,2)为待定参数。

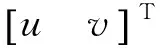
13)

这些单位矢量都在光心与图像直线l1和l2组成平面上,即满足式(12)。将式(13)代入式(12),化简可得:

(14)

式(14)对任意u都成立,因此:

(15)

式中ai、bi、ci为未知数。

由于式(12)等号右边为0,因此可以令bi=-Fy,代入式(15),求得ai、ci:

(16)

即根据跑道边缘线的图像可以确定光心和跑道边缘线组成平面方程在视觉测量坐标系内的表示。

借助式(2),将式(12)表示的平面转换到跑道坐标系(W系)内表示为:

i=1,2

(17)

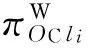
i=1,2

(18)

(19)

因此可以求得视觉测量系统位置的Y和Z分量,即利用跑道宽度可以提供高度(YW向)和偏离跑道中心线方向(ZW向)位置导航信息。

需要注意的是,在根据以上原理设计算法时需要考虑跑道边缘线图像l1和l2与YC轴近似平行情况,此时的l1和l2直线方程应该拟合成u=kiv+di(i=1,2)形式,相应的求解具体形式可以类似推导。

因此,已知姿态前提下,跑道宽度可以提供高度(YW向)和偏离跑道中心线方向(ZW向)位置导航信息。

从物理内涵上讲,上述结论不难理解。如图2所示,已知姿态前提下,可以确定视觉系统光心与跑道边缘线组成的两个平面,该两个平面的交线与跑道方向平行,确定了光心在高度方向(YW向)和跑道侧向(ZW向)的两个位置约束。

由2.1、2.2部分的分析,可以得到如下结论:

结论1:已知宽度的跑道边缘线可以提供如下姿态和位置视觉导航信息:俯仰角、偏航角、高度(YW向)和偏离跑道中心线方向(ZW向)位置。

3 地平线和跑道横向控制线视觉导航信息分析

由第2部分的分析可知,跑道边缘线提供的姿态和位置视觉导航信息都不完备,在实际应用中可进一步利用地平线和跑道横向控制线完善导航信息。

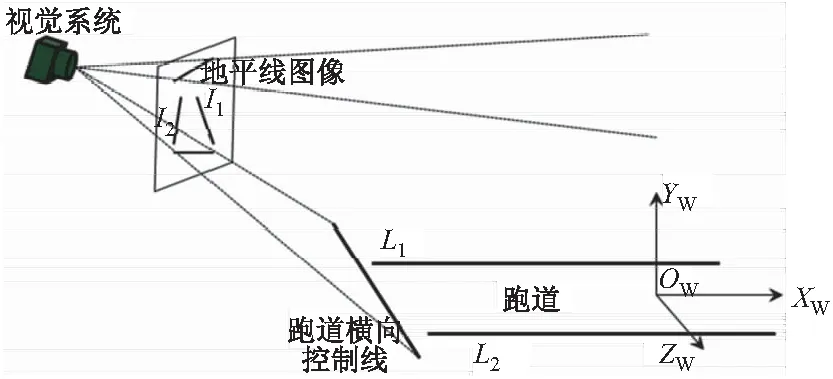
图3 地平线和跑道横向控制线成像示意图

3.1 地平线提供的姿态导航信息

若能够提取出视觉图像中的地平线,则可以以此确定视觉系统的滚转角和俯仰角。

假设地平线图像方程为:

v=k3u+d3

(20)

类似2.2部分的分析,可以得到光心与地平线确定的平面在跑道坐标系内的表示:

(21)

其中a3=k3Fx,b3=-Fy,c3=k3Cx-Cy+d3。

由于地平线在无穷远处,因此光心与地平线确定的平面方程(21)等价于如下方程:

m3yW+n3=0

(22)

因此有:

(23)

将姿态矩阵变换到等号右边,并写成单位向量的形式:

(24)

姿态矩阵仍按照2.1部分式(6)定义,则有:

(25)

由此可以求解出滚转角γ和俯仰角θ。

3.2 跑道横向控制线提供的姿态和位置导航信息

跑道横向控制线指跑道平面内垂直于跑道方向的特征线(如跑道底边、跑道进近横排灯线),其对应的XW坐标已知,控制线方程表示为:

(26)

假设跑道横向控制线对应图像直线的方程为:

v=k4u+d4

(27)

类似2.2部分的分析,可以得到视觉系统光心与跑道横向控制线确定的平面在跑道坐标系内的表示为:

(28)

其中a4=k4Fx,b4=-Fy,c4=k4Cx-Cy+d4。

根据跑道横向控制线方程(26),包含视觉系统光心和跑道横向控制线的平面在跑道坐标系的表示满足:

m4(xW-X0)+n4yW=0

(29)

其中m4和n4为待定系数。式(29)与方程(28)等价,因此:

(30)

1)跑道横向控制线提供的姿态信息

将式(6)代入式(30)的第三个等式可得:

(31)

由于跑道边缘线消隐点可以提供俯仰角θ和偏航角φ信息,再结合式(31),可以求解出滚转角γ。

2)跑道横向控制线提供的位置信息

由3.1、3.2部分的分析,可以得到如下结论:

结论2:地平线可以提供视觉滚转角和俯仰角导航信息;跑道横向控制线可以提供滚转角和跑道方向位置信息。

4 结论

文中针对基于跑道信息的无人机视觉着陆问题开展研究。不同于已有文献具体算法的设计,文中立足于从理论上分析无人机着陆中跑道能够提供的视觉信息,得到两个基本结论:

1)已知宽度的跑道边缘线可以提供如下姿态和位置视觉导航信息:俯仰角、偏航角、高度(YW向)和偏离跑道中心线方向(ZW向)位置。

2)地平线可以提供视觉滚转角和俯仰角导航信息;跑道横向控制线可以提供滚转角和跑道方向位置信息。

文中的研究对于进行基于跑道的视觉导航算法设计、精度分析和导航可观性分析等具有理论价值。

[1] SHARP C S, SHAKERNIA O, SASTRY S S. A vision system for landing an unmanned aerial vehicle [C]∥Proceedings of the 2001 IEEE International Conference on Robotics and Automation, 2001: 1720-1727.

[2] SASA S, GOMI H, NINOMIYA T,et al. Position and attitude estimation using image processing of runway: AIAA 2000-0301 [R]. 2000.

[3] 白亮, 陈袱, 膝科嘉. 计算机视觉辅助无人机自主着陆系统 [J]. 弹箭与制导学报, 2006, 26(2): 320-321.

[4] 张小苗. 机载视觉着陆导航测量方法及关键技术研究 [D]. 长沙: 国防科学技术大学, 2008: 129-150.

[5] 张广军, 周富强. 基于双圆特征的无人机着陆位置姿态视觉测量方法 [J]. 航空学报, 2005, 26(3): 344-348.

[6] 蔡鸣, 孙秀霞, 徐嵩. 视觉技术辅助的无人机自主着陆组合导航研究 [J]. 应用光学, 2015, 36(3): 343-350.

[7] 徐贵力, 倪立学, 程月华. 基于合作目标和视觉的无人飞行器全天候自动着陆导引关键技术 [J]. 航空学报, 2008, 29(2): 437-482.

[8] GUI Y, GUO P Y, ZHANG H L, et al. Airborne vision-based navigation method for UAV accuracy landing using infrared lamps [J]. Journal of Intelligent & Robotic Systems, 2013, 72(2): 197-218.

[9] ZHOU X, LEI Z H, YU Q F, et al. Videometric terminal guidance method and system for UAV accurate landing [C]∥Proc. SPIE 8387, Unmanned Systems Technobgy XIV，2012.

[10] 朱枫, 刘昶, 吴清潇. 视觉约束下无人机位姿参数的后验估计 [J]. 机器人, 2012, 34(4): 424-431.

[11] 庄丽葵, 丁萌, 曹云峰. 利用地平线与跑道边缘线估计无人机着陆参数 [J]. 传感器与微系统, 2010, 29(3): 104-108.

[12] 李飞, 谭乐祖, 唐亮. 基于跑道灯光的计算机视觉辅助无人机着陆 [J]. 兵工自动化, 2012, 31(1): 11-13.

Information Analysis of Vision Navigation Based on Runway

ZHANG Hongliang,GUO Pengyu

(College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China)

Vision navigation based on runway is a common application in landing an unmanned aerial vehicle (UAV). From the information point in vision navigation, observability of UAV attitude and position knowing edges of runway, horizon and transverse runway line were analyzed. Two conclusions about visual navigation information were deduced. It is proved that yaw, pitch, altitude and sideways position can be calculated by viewing edges of the runway known width, and with additionally viewing the horizon and the transverse runway line, complete attitude and position can be known. The research can be theoretically referred by method design, precision analysis and observability analysis of visual navigation based on runway.

vision navigation; runway; horizon; UAV landing

2015-10-12基金项目:国家自然科学基金(11272347)资助

张红良(1981-),男,江苏沛县人,讲师,博士,研究方向:摄像测量、视觉导航、惯性导航。

V249

A