基于元胞自动机演化的复杂电网脆弱性研究

梁志鹏，彭显刚，梁飞强，刘艺

( 广东工业大学 自动化学院，广东 广州510006)



基于元胞自动机演化的复杂电网脆弱性研究

梁志鹏，彭显刚，梁飞强，刘艺

( 广东工业大学 自动化学院，广东 广州510006)

摘要：根据元胞自动机理论在复杂系统中的应用，提出了一种新的复杂电网脆弱性评估方法——从元胞自动机的基本定义出发，建立复杂电力网络节点脆弱度指标的节点脆弱度元胞自动机模型，通过该模型演化得到节点脆弱度指标，并综合考虑电力网络的结构特性、功率特性和相邻节点间的相互影响。最后，通过IEEE 39节点系统仿真实现对节点脆弱度的排序，并通过与其它指标的对比验证了该模型的有效性和优越性。

关键词：元胞自动机;脆弱性评估;演化;电力网络

近年来，随着复杂性科学的快速发展，复杂网络理论已经深入应用于电网分析中。基于复杂网络理论的大型电力系统脆弱性研究作为新兴理论已被不少学者所研究。其中，节点的脆弱性研究一直是电力学术界和工程界关注的问题。

目前国内外相关学者主要从复杂网络理论[1-5]、信息理论[6-8]和电网运行参数[9-11]3个方面研究复杂电力系统脆弱性。文献[1]提出了在元件可靠性参数为权重的加权拓扑模型下，结合元件结构脆弱性的电网脆弱性评估模型。文献[2-4]提出了基于小世界拓扑模型的大型电网脆弱性评估方法。文献[5]从电网结构特征参数入手，研究了电网对不同类型的随机故障和蓄意攻击的承受能力。上述文献充分利用了复杂网络的各种理论获得了电网结构的脆弱环节，但其缺点在于所考虑的影响电网结构脆弱性的因素不全面，且目前的研究也仅处于理论阶段，离实际应用还有一定距离。文献[6]利用信息熵理论和关联聚类方法提出了复杂电力系统脆弱性的四层集合模型。文献[7]提出的基于加权结构熵和模糊综合评判的节点脆弱性评估指标可以定量评估电力系统组织结构特性对连锁故障传播的影响。文献[8]结合电力系统信息量的特点及系统安全约束对信息熵进行改进，提出一种考虑节点注入功率扰动的大型电力系统元件脆弱性评估方法。上述文献将信息熵理论应用于复杂电力系统脆弱性的研究中，但是熵理论与电力系统实际运行特点相结合方面仍有待深入研究。文献[9-10]以电力系统失负荷率作为衡量元件脆弱性的依据，建立电力系统脆弱性模型。文献[11]通过相邻节点平均负载均衡度和网络负载率参数融合的方法衡量失效节点对网络的影响，提出了一种耦合网络节点重要度评估方法。上述文献不仅从电力网络结构方面衡量元件脆弱性，并且考虑了电力负荷等电网运行参数的实际特点，更全面考虑了影响网络元件脆弱性的因素。

元胞自动机(cellular automaton, CA)[12]是研究复杂系统的方法之一。目前元胞自动机已被广泛应用于社会学、生物学、信息科学等研究领域中，在电力系统中的应用仍处于起步阶段。文献[13-15]分别将元胞自动机应用于空间负荷预测、复杂电力系统自组织临界特性和环网拓扑着色的研究中，其研究结果具有一定的实用价值。本文将CA理论应用于复杂电力系统节点脆弱性的研究中，构造了节点脆弱性CA模型，模型中每个元胞代表一个电网拓扑节点，通过元胞状态的演化研究相邻节点之间脆弱性的相互影响，最终达到电网脆弱节点辨识的目的。

1CA概述

CA是由大量元胞通过简单的局部相互作用而构成的时间和空间都离散的动力系统，分布在规则网格中的每一个元胞取有限的离散状态，遵循确定的局部规则作出同步更新[14]。CA不同于一般的动力学模型，它不是由严格的物理方程确定，而是通过构造一系列模型规则来实现，从而增强了其表达复杂关系的能力，为其在复杂系统脆弱性领域的研究与应用奠定了基础[16]。如图1所示，CA由元胞、元胞状态空间、邻居及局部演化规则4部分构成。

图1　元胞自动机的构成

CA还可以用数学式表示为

A=(Ld,S,N,f).

(1)

式中：A代表一个元胞自动机系统；Ld为元胞空间；d为元胞空间的维数；S为元胞的有限状态集合；N为一个所有邻域内元胞的组合，即一个包含n种不同元胞状态的空间矢量，记为N=(s1，s2，…，sn),n是元胞的邻居个数，si∈Z(Z为整数集合)，i∈{1, 2，…，n}；f表示将Sn映射到S上的一个状态转换函数。

2复杂电力网络节点脆弱度指标

衡量复杂网络特征的基本测度有特征路径长度、聚类系数、节点度以及节点/边介数等。其中节点度表示与该节点相连的节点数，如式(2)所示。将节点度值作为衡量网络中节点脆弱度的指标，即度指标Di，它能很好地反应网络节点的重要性，节点度值越大的节点在网络中的重要性越高。

(2)

式中的i与j有边的连接，则Dj为1，否则Dj为0。

已有的研究发现，电网结构脆弱性不仅与单纯电网拓扑结构的复杂网络特征参数相关，系统运行状态的变化也会对电网结构脆弱性产生不同的影响。因此，在应用复杂网络理论研究电力系统结构脆弱性时，需要在考虑网络特征参数的同时兼顾其系统运行状态。

文献[17]通过构建节点重要度函数来描述节点脆弱度指标，即

(3)

该指标同时考虑到节点的度和电力系统的功率特性，对电网脆弱性研究具有一定的实用价值。

在复杂系统自组织临界状态的研究中发现，连锁故障的传播是由元件之间的相互作用引起的。电力系统元件的脆弱性是这种连锁故障的内在机理。因此，节点的脆弱性与其在网络中所处的位置和相邻节点的作用密切相关。从复杂网络结构角度看，孤立节点对间不存在任何脆弱性传递或依赖关系。一旦节点间通过边连接，就可能导致节点脆弱度指标发生变化。本文通过节点脆弱度贡献函数K′i描述相邻节点脆弱度指标之间相互影响的关系，即

(4)

式中：n为节点数目；k为网络的平均度值；Dj为相邻节点j的度值；δji为相邻节点连边的权重。

综上所述，复杂电力网络的节点脆弱度指标为节点重要度函数和节点脆弱度贡献函数之和，即

Ei=Ki+K′i.

(5)

3节点脆弱度元胞自动机模型

3.1元胞自动机模型构成

根据电网拓扑化原则的描述，将发电机、负荷和变电站作为节点，输电线路及变压器支路作为边。因此，将电网中的发电机、负荷和变电站作为元胞，并看成是节点脆弱性元胞自动机中最基本的组成部分。

3.1.1元胞状态

元胞状态表示电网中的节点在演化过程中所处的状态，本模型中元胞的状态由元胞脆弱度指标决定。每个元胞有3种状态：“0”表示初始状态； “1”表示演化状态；“2”表示稳定状态。当所有元胞都处于稳定状态时，演化结束。

(6)

t≥1.

(7)

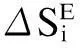
(8)

如式(8)所示，若元胞脆弱度指标变化率ΔSiE大于ξ，则元胞处于演化状态；若其小于ξ，则元胞处于稳定状态。

3.1.2元胞空间

元胞空间是指元胞所在空间的分布状态及连接关系的集合。本文通过电网的拓扑结构来确定每一个元胞的元胞空间。在节点脆弱性元胞自动机中，每一个元胞空间准确反应了节点在电网中的分布情况。

3.1.3元胞邻居

由于节点的脆弱性不仅与节点本身的重要度函数有关，还与相邻节点的脆弱度指标有关，其相互作用关系反应在转换规则中。因此，本文参考邻域半径r=1的Moore邻居模型，将元胞邻居定义为与该元胞直接相连的元胞。

3.1.4元胞的转换规则

转换规则是元胞自动机的关键，规则确定恰当否直接关系节点脆弱度指标是否准确。本文元胞状态的转换规则主要是通过元胞脆弱度指标变化率来确定。

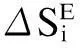
3.2元胞自动机演化流程

图2为节点脆弱度元胞自动机演化流程。其演化过程如下所述：

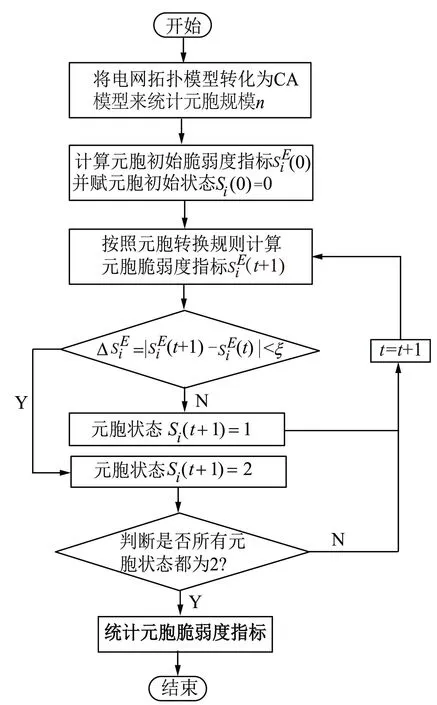
图2　元胞自动机演化流程

a)复杂电力网络拓扑模型转化成元胞自动机模型。将发电机、负荷、变电站等电力节点作为元胞，电力网络拓扑节点数为元胞规模。将电力输电线路和变压器支路作为与元胞直接相连的边，其等效电抗作为相邻元胞之间的边权重δ。

b)计算元胞脆弱度指标的初始值。将归一化处理后的节点重要度函数作为元胞初始脆弱度指标，并对元胞空间中所有的元胞赋于初始状态0。

c)开始元胞自动机演化。根据元胞转换规则计算演化后的元胞脆弱度指标，并判断元胞脆弱度变化率是否收敛，若收敛则元胞赋稳定状态2；若不收敛则元胞赋演化状态1。

d)稳定判据。第t代演化结束后，统计元胞空间中所有元胞的状态，若所有元胞都为稳定状态，则演化结束，否则继续进行第t+1代演化。

4算例分析

本文以IEEE 39节点系统为例进行算例分析，如图3所示。将系统中变压器等效支路视为线路来处理，并将线路电抗作为节点连边的权重δ，取ξ=0.000 01。

图3　IEEE 39节点系统接线

4.1节点脆弱性分析

使用本文提出的模型对系统进行脆弱性评估，图4为系统中节点脆弱度指标计算结果的分布,并分别给出了演化前各节点脆弱度指标的初始值和演化后的节点脆弱度指标。

图4　节点脆弱度指标分布图

从图4可以看出，经过节点脆弱度元胞自动机演化后的节点脆弱度指标变化很大，其中节点30至39的脆弱度指标变化较大，这是由于节点30至39为发电机节点，节点注入功率过大导致其初始脆弱度指标中功率特性过于突出，其脆弱性被节点的功率特性放大。经过节点脆弱度元胞自动机模型演化后，其相邻节点数过少的结构脆弱性慢慢的体现出来，最终导致其演化后的节点脆弱度指标下降很多。

本文将演化后的指标与演化前的指标、度指标和文献[18]的指标进行对比。由于篇幅有限，本文只列出节点脆弱度最高的10个节点，其排序见表1。

表1节点脆弱性排序

排序演化后指标初始指标度指标文献[18]指标1161616521766631539216421292611524103176522134719381910841922159262323710622913

从表1可以看出，4种指标评估结果差异很大，原因在于各种指标都是按特定的角度对节点的脆弱性进行关注。初始脆弱度指标考虑了网络的功率特性和结构特性，但是没有考虑相邻节点间的相互影响；度指标和文献[18]的指标都是从网络的结构特性进行评估，没有考虑到网络的功率特性。从4种指标的对比中可以看出，演化后的指标中节点21和24的脆弱度指标变化较大，原因是节点21的相邻节点16、23和节点24的相邻节点16、19的脆弱度指标较大，在演化过程中，其相邻节点之间的脆弱度贡献率较大。在实际电网中，若节点21和节点24发生故障，很有可能导致相邻的节点16发生故障，由于节点16是系统中脆弱度指标最高的关键节点，若其发生故障，则可能引起大规模连锁故障。

4.2评估结果验证

为了验证元胞自动机演化后节点脆弱度指标的有效性，将网络传输效能[19]E作为反映网络连通性的指标，即

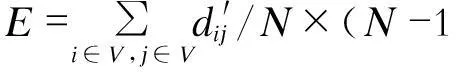
(9)

式中：d′ij为节点i与节点j之间最短路径长度的倒数；N为网络受到攻击后剩下的节点个数。

本文通过5种不同的攻击模式连续攻击脆弱度指标较高的7个节点，并计算被攻击后的网络传输效能。度指标攻击即为连续攻击系统中度指标较高的7个节点。以度指标攻击为例，首先攻击度指标最高的节点16，节点16受到攻击从系统中退出运行后，计算系统的网络传输能效，然后依次攻击度指标较高的6个节点并分别计算出节点受到攻击后系统的网络传输效能。其它攻击模式采用相同的攻击方法。图5为不同攻击模式下网络传输效能的对比。

图5　不同攻击模式下网络传输效能的变化

从图5可以看出，在随机节点攻击模式下，网络传输效能下降的最慢，在本文提出的演化后指标攻击模式下，网络传输效能下降最快。度指标、初始脆弱度指标和演化后指标均在第一次攻击时找到了导致网络传输效能下降最大的节点，但是经过多次攻击后，初始脆弱度指标和度指标攻击模式下的网络传输效能变化不大。文献[18]指标在多次攻击下，网络传输效能下降很快，但是其并没有在第一次攻击时找到导致网络传输效能下降最快的关键节点。通过不同攻击模式下网络传输效能的对比，可以看出本文指标的有效性和优越性。

5结束语

本文将元胞自动机理论引入复杂电力网络节点脆弱性的研究中，建立了通过元胞自动机演化得到节点脆弱度指标的节点脆弱度元胞自动机模型。针对元胞自动机元胞状态为有限离散状态集合的局限性，模型中没有将节点脆弱度指标作为元胞状态，而是将元胞的不同演化阶段作为元胞状态。通过定义脆弱度指标变化率和收敛域获得元胞自动机的转换规则，经过演化后使元胞达到稳定状态，从而获得节点脆弱度指标。

通过示例仿真和不同攻击模式下的对比，验证了该模型演化后得到节点脆弱度指标的有效性和优越性，为复杂电力网络脆弱性的研究提供了一个新的研究思路。

参考文献：

[1] 魏振波，刘俊勇，朱国俊，等.基于可靠性加权拓扑模型下的电网脆弱性评估模型[J].电工技术学报，2010,25(8):131-137.

WEI Zhenbo,LIU Junyong, ZHU Guojun, et al. Vulnerability Evaluation Model to Power Grid Based on Reliability-Parameter-Weighted Topological Model[J]. Transactions of China Electrotechnical Society, 2010, 25(8): 131-137.

[2] 丁明，韩平平.基于小世界拓扑模型的大型电网脆弱性评估算法[J].电力系统自动化，2006,30(8):7-10.

DING Ming, HAN Pingping. Small-world to Pological Model Based Vulnerability Assessment Algorithm for Large-scale Power Grid[J]. Automation of Electric Power Systems,2006,30(8):7-10.

[3] 丁明，韩平平.加权拓扑模型下的小世界电网脆弱性评估[J].中国电机工程学报，2008,28(10):20-25.

DING Ming, HAN Pingping. Vulnerability Assessment to Small-world Power Grid Based on Weighted Topological Model[J]. Proceedings of the CSEE, 2008, 28(10):20-25.

[4] 丁剑，白晓民，赵伟，等.基于二维平面拟合的电网脆弱性分析[J].电力系统自动化，2008,32(8):1-4.

DING Jian,BAI Xiaomin, ZHAO Wei，et al. Grid Vulnerability Analysis Based on Two-dimensional Accumulation Means[J]. Automation of Electric Power Systems, 2008,32(8):1-4.

[5] 张国华，张建华，杨京燕，等.基于有向权重图和复杂网络理论的大型电力系统脆弱性评估[J].电力自动化设备，2009,29(4):21-26.

ZHANG Guohua,ZHANG Jianhua, YANG Jingyan，et al. Vulnerability Assessment of Bulk Power Grid based on Weighted Directional Graph and Complex Network Theory[J].Electric Power Automation Equipment, 2009,29(4):21-26.

[6] 尹项根，陈庆前，王博，等.基于四层集合模型的复杂电力系统脆弱性评估体系[J].电工技术学报，2013,28(1):225-233.

YIN Xianggen, CHEN Qingqian, WANG Bo, et al. Vulnerability Assessment System of Complicated Power System Based on Four-Level Set Model[J]. Transactions of China Electrotechnical Society, 2013,28(1):225-233.

[7] 蔡晔，曹一家，谭玉东，等.基于标准化结构熵的电网结构对连锁故障的影响[J].电工技术学报，2015,30(3):36-43.

CAI Yei, CAO Yijia, TAN Yudong, et al. Influences of Power Grid Structure on Cascading Failure Based on Standard Structure Entropy[J]. Transactions of China Electrotechnical Society, 2015, 30(3): 36-43.

[8] 靳冰洁，张步涵，姚建国，等.基于信息熵的大型电力系统元件脆弱性评估[J].电力系统自动化，2015,39(5):61-68.

JIN Bingjie, ZHANG Buhan, YAO Jianguo, et al.Large-scale Power System Components Vulnerability Assessment Based on Entropy[J]. Automation of Electric Power Systems,2015,39(5):61-68.

[9] 李扬，苏慧玲.N-k故障下影响电力系统脆弱性的关键线路研究[J].电力自动化设备，2015,35(3):60-67.

LI Yang,SU Huiling. Critical Line Affecting Power System Vulnerability underN-kContingency Condition[J]. Electric Power Automation Equipment, 2015,35(3):60-67.

[10] 苏慧玲，李扬.从电力系统复杂网络特征探讨元件的脆弱性[J].电力系统自动化，2012,36(23):12-17.

SU Huiling,LI Yang.Electrical Component Vulnerability Analysis from Complex Network Characteristics of Power Systems[J].Automation of Electric Power Systems,2012,36(23):12-17.

[11] 吴润泽，张保健，唐良瑞.双网耦合模型中基于级联失效的节点重要度评估[J].电网技术，2015,39(4):1053-1058.

WU Runze, ZHANG Baojian,TANG Liangrui. A Cascading Failure Based Nodal Importance Evaluation Method Applied in Dual Network Coupling Model[J]. Power System Technology,2015,39(4):1053-1058.

[12] WOLFRAM S. Theroy and Applications of Cellular Automata[M].Singapore:World Scientific Press,1986.

[13] 刘自发，庞铖铖，王泽黎，等. 基于云理论和元胞自动机理论的城市配电网空间负荷预测[J].中国电机工程学报，2013,33(10):98-105.

LIU Zifa, PANG Chengcheng, WANG Zeli, et al. Spatial Load Forecasting for Distribution Network Based on Cloud Theory and Cellular Automata[J]. Proceedings of the CSEE, 2013,33(10):98-105.

[14] 于群，曹娜，郭剑波.基于元胞自动机的电力系统自组织临界特性仿真模型[J].电力系统自动化，2011,35(21):1-5.

YU Qun, CAO Na,GUO Jianbo. Power System Self-organized Criticality Simulation Model Based on Cellular Automata[J]. Automation of Electric Power Systems, 2011,35(21):1-5.

[15] 屈志坚，刘明光，刘靖，等.基于元胞自动机演化的环网拓扑着色新算法[J].电力自动化设备，2012,32(7):76-82.

QU Zhijian,LIU Mingguang, LIU Jing, et al. Topology Coloring Algorithm Based on Cellular Automata Evolution for Loop-nested Network[J]. Electric Power Automation Equipment,2012, 32(7):76-82.

[16] 张永安，白志学. 复杂系统的重要研究工具—细胞自动机及其应用[J].自然杂志,1998, 20(4):192-196.

ZHANG Yong’an, BAI Zhixue. A Important Tool for Complex System Research-cellular Automata and Its Application[J].Nature Magazine,1998,20(4):192-196.

[17] 肖盛.基于风险理论的电网脆弱性评估[D].北京：华北电力大学，2011.

[18] 邓春兰.基于复杂网络理论的电网连锁故障脆弱性研究[D].成都：西南交通大学,2014.

[19] 潘高峰.基于复杂网络理论的电网脆弱性研究[D].广州：广东工业大学，2014.

梁志鹏(1990)，男，河南焦作人。在读硕士研究生，从事电力系统运行分析与控制研究工作。

彭显刚(1964)，男，湖北武汉人。副教授，硕士生导师，工学硕士，主要从事电力系统优化运行与控制方面的研究与教学工作。

梁飞强(1988)，男，湖北咸宁人。在读硕士研究生，从事电力系统运行分析与控制研究工作。

(编辑王夏慧)

新 年 快 乐，吉 祥 如 意！

Research on Vulnerability of Complex Power Grid Based on Cellular

Automata Evolution

LIANG Zhipeng, PENG Xiangang, LIANG Feiqiang, LIU Yi

(School of Automation, Guangdong University of Technology, Guangzhou, Guangdong 510006, China)

Abstract：According to application of cellular automata theory in complex system, a kind of new evaluation method for vulnerability of complex power grid is proposed which starts from basic concept of cellular automata and establishes a cellular automata model for node vulnerability of node vulnerability index of the electric power network, by evolution of which it is able to get node vulnerability index and comprehensively consider of structure characteristic, power characteristic and interactive effect of adjacent nodes of the electric power network. Finally, by means of IEEE 39 node system, sorting for node vulnerability is realized, and comparison with other index proves effectiveness and superiority of this model.

Key words：cellular automata; vulnerability evaluation; evolution; electric power network

作者简介：

基金项目：中国南方电网公司科技项目(K-GD2014-0891)。

收稿日期：2015-08-11修回日期：2015-10-16

中图分类号：TM711

文献标志码：A

文章编号：1007-290X(2016)01-0045-06

doi:10.3969/j.issn.1007-290X.2016.01.010