带有输入加性时滞的切换系统的异步H∞控制

李莉莉，金翠丽，苑春波

(辽宁师范大学 数学学院，辽宁 大连 116029)



带有输入加性时滞的切换系统的异步H∞控制

李莉莉，金翠丽，苑春波

(辽宁师范大学 数学学院，辽宁 大连 116029)

摘要：研究一类输入中带有两个加性时变时滞的切换系统的异步H∞控制问题。控制器切换信号的时变延时导致子系统和控制器切换不同步。针对两类延时,基于平均驻留时间(ATD)方法和合并切换信号技术,构造仅在系统模态和控制器模态匹配时下降的Lyapunov-Krasovskii (L-K)泛函。结合两种积分不等式,充分利用加性时滞信息的基础上引入较少的松弛矩阵,避免耦合线性矩阵不等式计算复杂,得到一种保守性较低的状态反馈控制器。系统在相应的平均驻留时间内的任意切换信号下异步H∞问题可解。最后数值例子验证了结论的有效性。

关键词：异步切换；输入加性时滞；H∞控制；平均驻留时间(ADT)

时滞是实际系统中一种无法避免的现象,时滞的存在会导致系统性能变差甚至不稳定,因此切换时滞系统的研究具有重要的理论价值和实际意义。在切换时滞系统的研究中,ADT方法因切换规则设计的灵活性倍受青睐[1-4]。现有文献较少考虑系统接收切换信号至实施切换动作过程中的延时。文献[5]讨论了一类状态中含有常时滞的Lipschitz非线性切换系统的异步鲁棒控制问题,当切换信号存在有界常时延时,使用驻留时间方法得到系统指数稳定的条件。文献[3]基于ADT方法和半正定规划方法得到切换信号发生常延时的一类输入时滞系统指数稳定的条件。与文献[3,5]得到两组耦合的矩阵不等式不同,文献[4]研究一类切换信号带有时变延时的输入常时滞切换系统的异步H∞控制问题,构造含有一重积分的新L-K泛函,所得稳定性条件中非耦合的线性矩阵不等式降低了计算的复杂度。加性时滞有着广泛的实际背景,如网络控制系统中的信号传递过程。从传感器到控制器的延时同控制器到执行器的延时性质不同,将两种延时直接加和处理是不合理的,因此加性时滞系统稳定性的分析应该充分考虑两种延时的时滞信息[6]。文献[7-10]采用几种不同形式的Jensen积分不等式的变形形式讨论了几类加性时滞系统的稳定性。文献[8]引进自由权矩阵方法构造新L-K泛函,得到低保守性的稳定条件;文献[9]和[10]通过分解时滞增加稳定性条件中的时滞信息,降低结论的保守性;文献[11]将加性时滞引入切换系统,讨论一类加性时滞切换系统的加权H∞滤波问题。

本文针对一类输入中带有两个加性时变时滞的切换系统,考虑控制器的切换滞后导致的子系统和控制器的不同步,研究异步H∞控制问题。首先,针对加性时滞和切换信号的延时,基于ADT方法和合并切换信号技术,构造新的L-K泛函。新泛函只要求在系统模态和控制器模态匹配时是下降的,同时一重积分项和二重积分项的使用增加了系统时滞信息。然后,结合两种积分不等式处理泛函沿系统导数中的交叉项,充分利用加性时滞信息并引入较少的松弛矩阵,得到系统在一种保守性较低的异步控制器及相应的平均驻留时间内的任意切换信号下指数稳定且具有L2增益的充分条件。导出的不等式在不同切换状态下是非耦合的,这对降低计算的复杂性有积极作用。最后数值例子检验了文中结果的有效性。

1系统描述及引理

考虑如下形式的一类切换系统

(1)

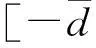
u(t)=Kσ(t-ds(t))x(t-d1(t)-d2(t)),

(2)

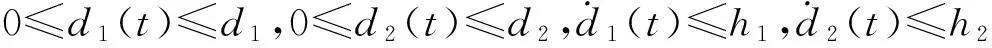
(3)

注1在实际系统中,信号从一个节点到另一个节点可能经历几段网络,产生不同属性的延时。将这些时滞的和作为一个时变时滞处理显然不合理;即便是具有相同属性的时滞,它们和也不一定在每个时滞取最大值时达到最大。因此,式(2)中的加性时滞具有更广泛、更合理的应用背景。

下面给出本文证明过程中将用到的定义及引理。

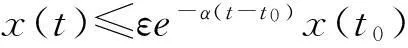
定义2系统(1)的异步H∞控制问题可解,若存在形如(2)的控制器和满足ADT的异步切换规则使得

(i)当w(t)=0时,系统(3)是指数稳定的;

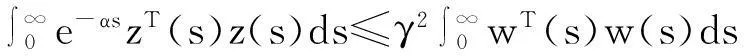
定义3[4]对任意的t2>t1≥0,令Nσ(t1,t2)为系统在区间(t1,t2)上的切换次数,若对于N0≥0,τα>0,有Nσ(t1,t2)≤N0+(t2-t1)/τα成立,则称τα为平均驻留时间。Save[τα,N0]表示由τα和N0确定的切换信号集合。

引理1[12]对取定的σ1(t)∈Save[τα,N0]和σ2(t)=σ1(t-ds(t))(0≤ds(t)≤ds)有

(i)σ2(t)∈Save[τα,N0+(ds/τα)];

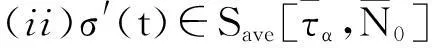
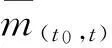
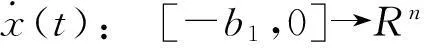
引理4[14]设0≤d(t)≤b2,其中d(t):R+→R+,对任意的Z=ZT>0,如下不等式成立:

引理5[15]假设γ1≤γ(t)≤γ2,式中γ(·):R+→R+,对于任意适当维数的常数矩阵Ξ1，Ξ2和Ξ,Ξ+(γ(t)-γ1)Ξ1+(γ2-γ(t))Ξ2<0当且仅当Ξ+(γ2-γ1)Ξ1<0,Ξ+(γ2-γ1)Ξ2<0。

2主要结果

本节给出系统(1)在控制器(2)下的异步H∞控制问题可解的充分条件。

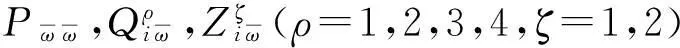
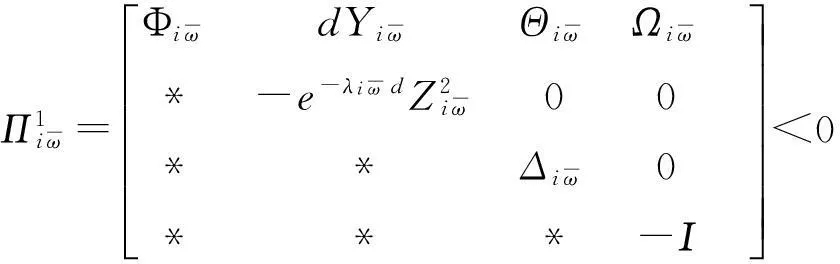
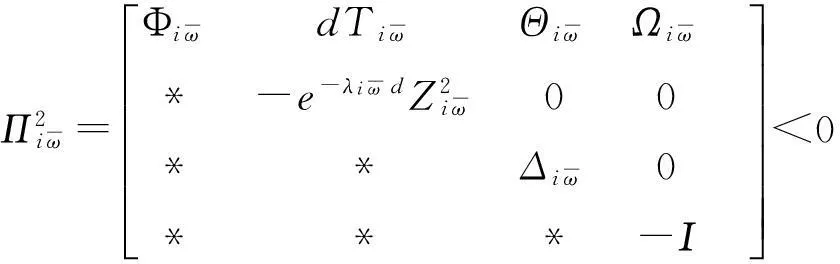
(4)

则存在形如(2)的状态反馈控制器确保系统(1)在平均驻留时间τα满足

(5)

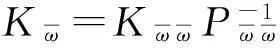
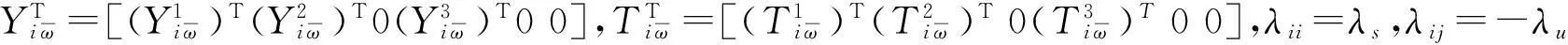
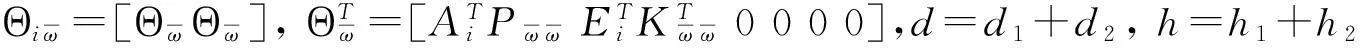
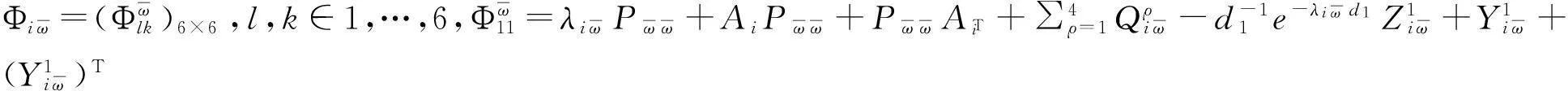
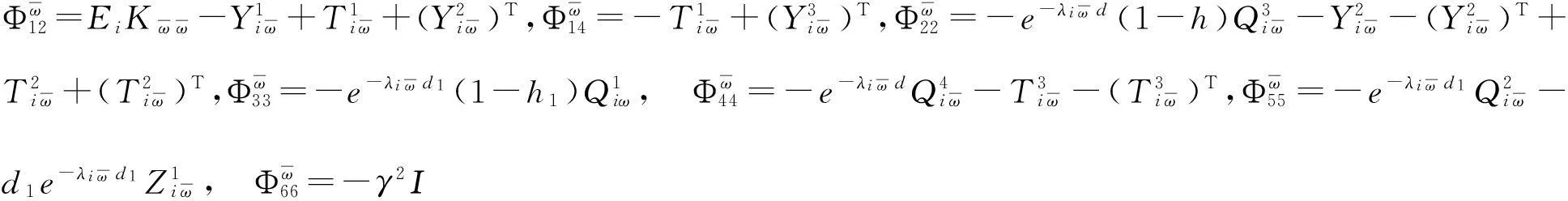
证明由于控制器中存在切换信号时滞ds(t),当系统从第j个子系统切换到第i个子系统时,控制器Kj仍处于激活状态。此时将切换系统(1)可改写成如下形式：

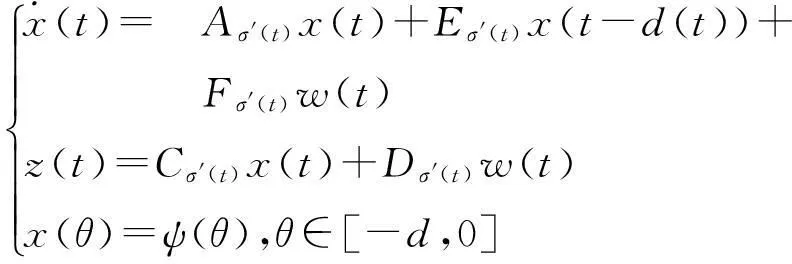
(6)

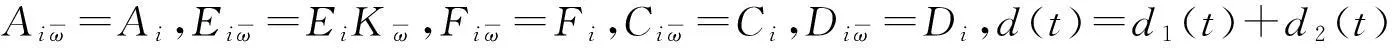
(7)

由引理5可知，Σii<0当且仅当

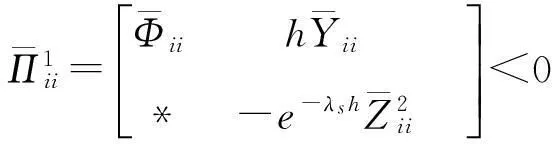
(8)

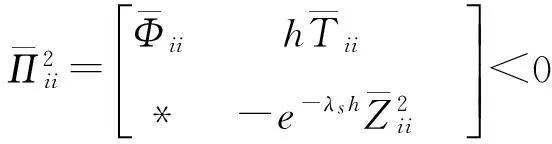
(9)

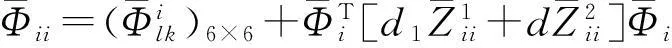
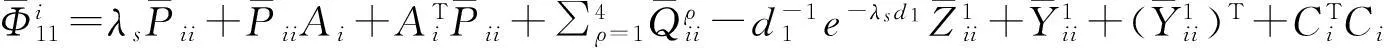
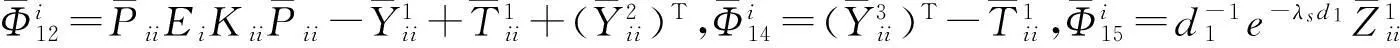
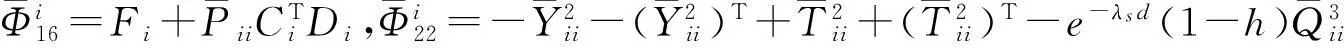
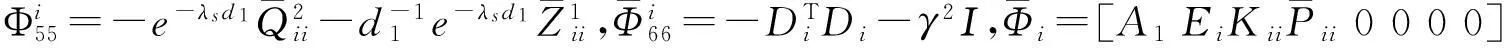
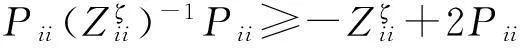
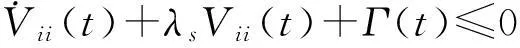
(10)

同理可知

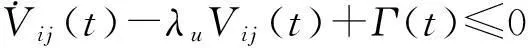
(11)

同时考虑(4)和(7),可以得到

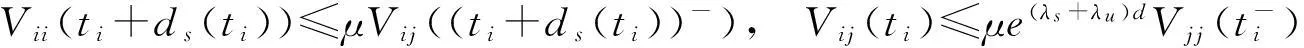
(12)

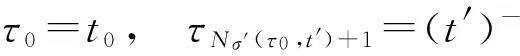
(13)

使用(12)对(13)进行迭代可以得到

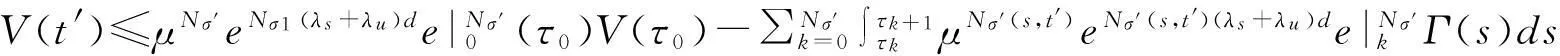
(14)

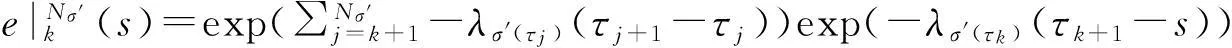
(15)

由(5)知存在λ使得2lnμ/τα+(λs+λu)d/τα<λ<λs-(λs+λu)ds/τα,即

(λs+λu)ds<(λs-λu)τα,λ[2lnμ+(λs+λu)d]/τα。

(16)

所以同时考虑(14)-(16)和引理2可得

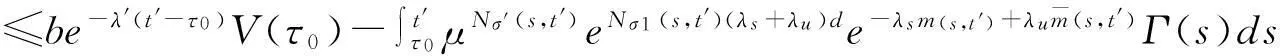
(17)

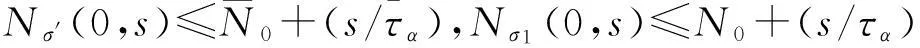
注2所构造的L-K泛函(7)只要求在系统模态和控制器模态匹配时是下降的。此外(7)中引入了二重积分项,充分利用了时滞信息,能够有效地降低所得结果的保守性。

注3定理1使用了引理3和引理4中的两种积分不等式来处理泛函沿系统导数中的交叉项,充分考虑时滞信息的同时引入了较少的松弛矩阵,降低了计算量。

注4一些文献[8,10]得到的不等式是耦合的,求解过程复杂。基于本文构造的L-K泛函,定理1中导出的不等式在不同切换状态下是非耦合的,有效降低了计算的复杂性。

当控制器(2)中切换信号延时ds(t)=0时,有以下同步切换的结果。

3数值例子

本节将通过数值例子验证文中提出的结论的有效性。考虑含有两个子系统的切换系统为:

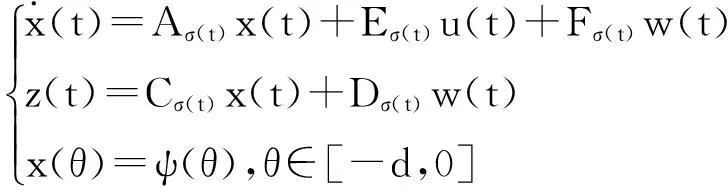
式中，σ(t):[0,∞)→M={1,2},

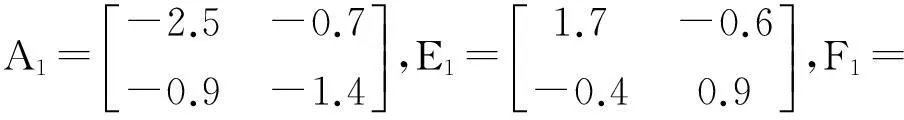
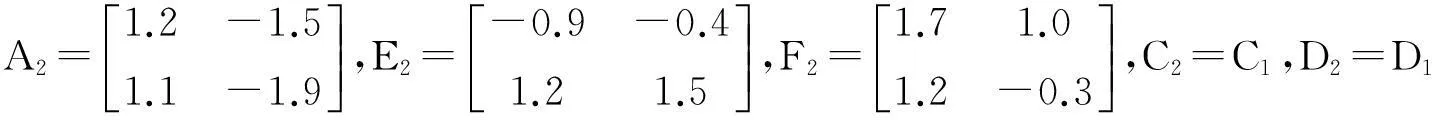
取μ=1.51,λs=0.6,λu=0.5,d1=0.2,d2=0.3,h1=0.2,h2=0.3,使用MATLAB的LMI工具箱求解定理1中的线性矩阵不等式组，可知上述系统异步H∞控制问题可解，同时求得控制器增益

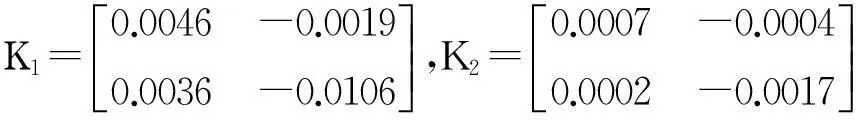
x0=[102]T时,相应的闭环系统的状态响应如图2。

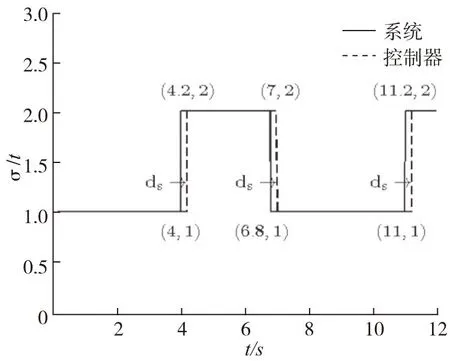
图1　切换信号

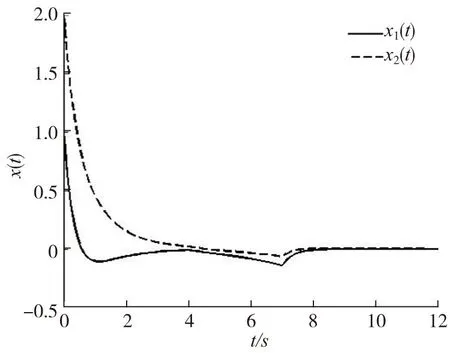
图2　状态反馈

4结语

本文考虑了一类时滞切换系统的异步H∞控制问题。系统的控制输入中带有两个加性时变时滞,并且控制器的切换信号中也存在时变延时。根据ADT方法和合并切换信号技术,通过构造包含更多时滞信息的L-K泛函,建立了系统在异步H∞控制器及相应的切换规则下指数稳定且具有L2增益的充分条件。新泛函不仅对系统模态和控制器模态不匹配时没有严格要求,能有效降低结论的保守性,还保证了导出的不等式在不同切换状态下是非耦合的,从而降低了计算的复杂性。引理4的使用,在保留更多加性时滞信息的同时引入了较少的松弛矩阵,对降低计算的复杂度有积极作用。最后通过一个数值例子验证了文中主要结果的有效性。

参考文献：

[1]ZHAIG,HUB,YASUDAK.Disturbanceattenuationpropertiesoftime-controlledswitchedsystems[J].JournaloftheFranklinInstitute, 2001, 338(7): 765-779.

[2]SUNXM,ZHAOJ,HILLDJ.StabilityandL2-gainanalysisforswitcheddelaysystems:adelay-dependentmethod[J].Automatica, 2006, 42(10): 1769-1774.

[3] 刘正凡, 蔡晨晓, 殷明慧, 等. 切换时滞系统的时滞反馈镇定[J]. 南京理工大学学报(自然科学版) 2014, 38(2): 291-298.

[4]WANGYE,SUNXM,ZHAOJ.AsynchronousH∞controlofswitcheddelaysystemswithaveragedwelltime[J].JournaloftheFranklinInstitute, 2012, 349(10): 3159-3169.

[5]XIANGZR,WANGRH.Robustcontrolforuncertainswitchednon-linearsystemswithtimedelayunderasynchronousswitching[J].IETControlTheoryandApplications, 2009, 3(8): 1041-1050.

[6]LAMJ,GAOH,WANGC.Stabilityanalysisforcontinuoussystemswithtwoadditivetime-varyingdelaycomponents[J].SystemsandControlLetters, 2007, 56(1): 16-24.

[7]SHAOH,HANQL.Onstabilizationforsystemswithtwoadditivetime-varyinginputdelaysarisingfromnetworkedcontrolsystems[J].JournaloftheFranklinInstitute, 2012, 349(6): 2033-2046.

[8]LIT,TIANJ.Convexpolyhedronmethodtostabilityofcontinuoussystemswithtwoadditivetime-varyingdelaycomponents[J].JournalofAppliedMathematics, 2012,ArticleID689820, 13pages.

[9]ZHUXL,WANGY,DUX.Stabilitycriteriaforcontinuous-timesystemswithadditivetime-varyingdelays[J].OptimalControlApplicationsandMethods, 2014, 35(2): 166-178.

[10]XIONGL,YANGF,CHENX.Newstabilizationfordynamicalsystemwithtwoadditivetime-varyingdelays[J].TheScientificWorldJournal, 2014,ArticleID315817, 8pages.

[11]LILL,ZHANGG,GEX,etal.WeightedH∞filteringforaclassofswitchedlinearsystemswithadditivetime-varyingdelays[J].MathematicalProblemsinEngineering, 2015,ArticleID649487, 11pages.

[12]VUL,MORGANSENKA.Stabilityoftime-delayfeedbackswitchedlinearsystems[J].IEEETransactionsonAutomaticControl, 2010, 55(10): 2385-2390.

[13]HANQL.Absolutestabilityoftime-delaysystemswithsector-boundednonlinearity[J].Automatica, 2005, 41(12): 2171-2176.

[14]RAMAKRISHNANK,RAYG.Robuststabilitycriteriaforuncertainneutralsystemswithintervaltime-varyingdelay[J].JournalofOptimizationTheoryandApplications, 2011, 149(2): 366-384.

[15]YUED,TIANE,ZHANGY.Apiecewiseanalysismethodtostabilityanalysisoflinearcontinuous/discretesystemswithtime-varyingdelay[J].InternationalJournalofRobustandNonlinearControl, 2009, 19(13): 1493-1518.

(责任编辑王楠楠)

Asynchronous H∞Control for Switched Systems with Input Additive Delays

LI Li-li，JIN Cui-li，YUAN Chun-bo

(School of Mathematics, Liaoning Normal University, Dalian Liaoning 116029, China)

Abstract:The asynchronous H∞control is studied for a class of switched systems with two input additive time-varying delays. The time-varying delay in the switching signal of the controllers causes the asynchronous switching between the subsystems and the controllers. According to two types of delay, based on the modes of average dwell time (ADT) method and the merging switching signal technique, a Lyapunov-Krasovskii (L-K) function is constructed to descent only when the subsystems and the controllers are mode matching. By combining two kinds of the integral inequality, less slack matrices are introduced based on the full use of more additive delay information, avoiding coupled linear matrix inequalities technique calculation complexity, a less conservative state feedback controller is obtained. The asynchronous H∞control of the system is solved under arbitrary switching signal satisfying the corresponding ADT scheme. Finally, a numerical example verifies the effectiveness of the conclusion.

Key words:asynchronous switching；input additive delays；H∞control；average dwell time (ADT)

中图分类号：TP13

文献标志码：A

文章编号：2096-1383(2016)01-0078-06

作者简介：李莉莉(1982-)，女，辽宁大连人，副教授，博士，主要从事切换系统控制理论研究。

基金项目：国家自然科学 (61304056);辽宁省教育厅科学技术研究项目(L2013409)。

收稿日期：2015-06-25；最后修回日期：2015-11-16