Colored-Motzkin数对数凸性研究

王善坤，张治海

(大连理工大学 城市学院，辽宁 大连 116600)



Colored-Motzkin数对数凸性研究

王善坤，张治海

(大连理工大学 城市学院，辽宁 大连 116600)

摘要：通过构造Colored-Motzkin三角矩阵，验证了该矩阵为Aigner-Catalan-Riordan矩阵的特例。通过证明Colored-Motzkin数是Colored-Motzkin三角矩阵的第0列元素来研究其对数凸性。由于Catalan数、Motzkin数、Hexagonal数都是Colored-Motzkin数的特例，因此可以统一的推导出Catalan数、Motzkin数、Hexagonal数各自都构成对数凸序列。

关键词：Colored-Motzkin数；Aigner-Catalan-Riordan矩阵；对数凸性

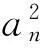
组合学家们在组合序列的对数凹性方面已经取得了丰富的研究成果[3-4]。而在组合序列的对数凸性方面，情况并不是一样的乐观。Davenport 和 Pólya[5]于1949年得出二项式卷积保持对数凸性的结论，但是在很长一段时间里，组合学家们并没有对序列的对数凸性进行非常系统的研究。因此目前只有一些比较零散的研究结果。本文研究带有参数的组合序列Colored-Motzkin数的对数凸性，由于Colored-Motzkin数可以统一的表示许多常见的组合序列，因此可以统一的判断许多常见组合序列是否具有对数凸性。

1Colored-Motzkin数及相关工具简介

1.1　Colored-Motzkin数

Colored-Motzkin数mn(u,l,d)[6]定义为

式中，u,l,d为非负整数。 mn(u,l,d)满足递归关系

(n+2)mn(u,l,d)=l(2n+1)mn-1(u,l,d)+(4ud-l2)(n-1)mn-2(u,l,d)。

由上式可以得出Colored-Motzkin数的发生函数为[7]

1.2　Riordan矩阵

Riordan矩阵是无限下三角矩阵，该矩阵可以用一对函数(g(x),f(x))来表示。Riordan矩阵第k列元素的发生函数Ck(x)为

Ck(x)=xkfk(x)g(x), k=0,1,2,…,

式中，g(0)=1,f(0)≠0。

设R=[rn,k]n,k≥0为Riordan矩阵，且R=(g(x),f(x))。则Riordan矩阵R可以通过序列A={an}n≥0和Z={zn}n≥0来刻画[8]，即

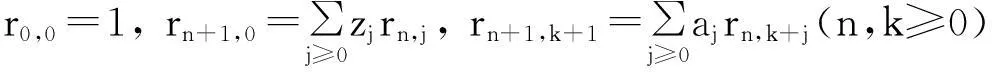
设A序列的发生函数为A(x)，Z序列的发生函数为Z(x)，则A(x)和Z(x)与g(x)和f(x)满足关系

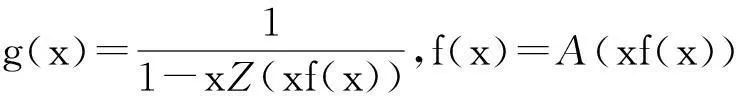
1.3　Aigner-Catalan-Riordan矩阵

设矩阵

是无限下三角矩阵，其满足递归关系

(n,k≥0),

式中，zj,aj,k为非负整数，且当k>j≥0时 aj,k=0。无限下三角矩阵T=[tn,k]n,k≥0称为Aigner-Catalan-Riordan矩阵。

设矩阵T=[tn,k]n,k≥0为Aigner-Catalan-Riordan矩阵，则称矩阵

为Aigner-Catalan-Riordan矩阵T=[tn,k]n,k≥0的系数矩阵。容易看出Aigner-Catalan-Riordan矩阵是广义的Riordan矩阵。

2Colored-Motzkin数的对数凸性

定义1Colored-Motzkin三角矩阵M(u,l,d)=[Mn,k(u,l,d)]n,k≥0是无限下三角矩阵，其递归定义为

M0,0(u,l,d)=1, T0,k(u,l,d)=0 (k>0);

Tn+1,0(u,l,d)=lTn,0(u,l,d)+dTn,1(u,l,d) (n≥0);

Tn+1,k+1(u,l,d)=uTn,k(u,l,d)+lTn,k+1(u,l,d)+dTn,k+2(u,l,d) (n,k≥0)。

其中u,l,d为非负整数。

定理1Colored-Motzkin数mn(u,l,d)是Colored-Motzkin三角矩阵M(u,l,d)=[Mn,k(u,l,d)]n,k≥0的第0列元素。

证明由Riordan矩阵的定义可得Colored-Motzkin三角矩阵M(u,l,d)=[Mn,k(u,l,d)]n,k≥0是Riordan矩阵的特例，且其A序列与Z序列分别为

A={u,l,d,0,…},Z={l,d,0,…};

其A序列与Z序列的发生函数分别为

A(x)=u+lx+dx2,Z(x)=l+dx。

设M(u,l,d)=(g(x),f(x))，则由A(x)和Z(x)与g(x)和f(x)之间满足的关系可得

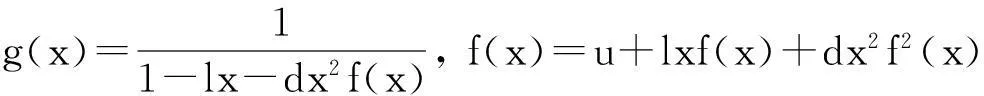
由f(0)=c可以解得

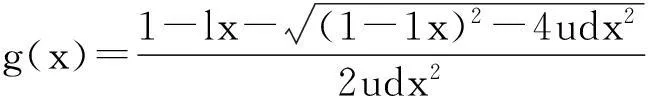
将式g(x)与Colored-Motzkin数的发生函数进行比较，可得Colored-Motzkin数mn(u,l,d)是Colored-Motzkin三角矩阵M(u,l,d)=[Mn,k(u,l,d)]n,k≥0的第0列元素，即

mn(u,l,d)=Mn,0(u,l,d)。

证毕。

定理2[9]设矩阵T=[tn,k]n,k≥0为Aigner-Catalan-Riordan矩阵，若该矩阵的系数矩阵[ζ,A]是TP2矩阵， 则矩阵T的第0列元素构成对数凸序列。

定理3当l2≥ud时，Colored-Motzkin数mn(u,l,d)构成对数凸序列。

证明由Colored-Motzkin三角矩阵M(u,l,d)=[Mn,k(u,l,d)]n,k≥0的定义可得矩阵M(u,l,d)是Aigner-Catalan-Riordan矩阵的特例，其系数矩阵为

易见当l2≥ud时系数矩阵[ζ,A]是TP2矩阵。最后由定理2可得当l2≥ud时，Colored-Motzkin数mn(u,l,d)构成对数凸序列。

证毕。

3结语

通过研究Colored-Motzkin数的对数凸性，可以统一的研究Catalan数、Motzkin数、Hexagonal数的对数凸性，统一相关结论。

当u=1,l=1,d=1时，

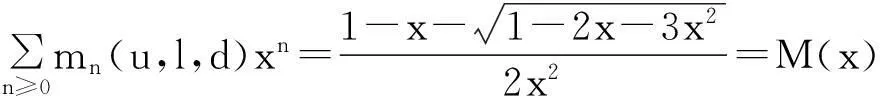
当u=1,l=2,d=1时，

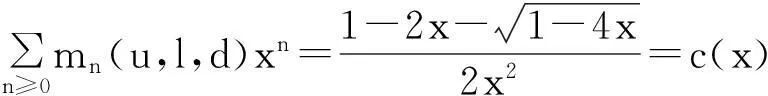
当u=1,l=3,d=1时，

可见Colored-Motzkin数是Catalan数、Motzkin数、Hexagonal数的共同推广[10]，即

Mn(1,1,1)=Mn;

Mn(1,2,1)=Cn+1;

Mn(1,3,1)=Hn。

推论1Catalan数、Motzkin数、Hexagonal数各自都构成对数凸序列。

参考文献：

[1]DOLIC′T,SVRTAND,VELJAND.Enumerativeaspectsofsecondarystructures[J].DiscreteMath, 2004, 285(1/2/3):67-82.

[2]ASAIN,KUBOI,KUOHH.Bellnumbers,log-concavity,andlog-convexity[J].ActaApplMath, 2000, 63(1/2/3):79-87.

[3]STANLEYRP.Log-concaveandunimodalsequencesinalgebra,combinatorics,andgeometry[G]∥GraphTheoryanditsApplications:EastandWest.NewYork:NewYorkAcadSci, 1989: 500-535.

[4]BRENTIF.Log-concaveandunimodalsequencesinalgebra,combinatorics,andgeometry:anup-date[G]∥Jerusalemcombinatorics’93.vol178.AmerMathSoc,Providence,RI, 1994: 71-89.

[5]DAVENPORTH,PóLYAG.Ontheproductoftwopowerseries[J].CanadianJMath, 1949, 1:1-5.

[6]MANSOURT,SCHORKM,SUNY.Motzkinnumbersofhigherrank:generatingfunctionandexplicitexpression[J].JIntegerSeq, 2007, 10(7):Article07.7.4, 11.

[7]WILFHS.Generatingfunctionology[M].Boston:AcademicPress,Inc, 1990.

[8]MERLINID,ROGERSDG,SPRUGNOLIR,etal.OnsomealternativecharacterizationsofRiordanarrays[J].CanadJMath, 1997, 49(2):301-320.

[9]WANGY,ZHANGZH.Log-convexityofAigner-Catalan-Riordannumbers[J].LinearAlgebraAppl,2014, 463:45-55.

[10]WANGY,ZHANGZH.Combinatoricsofgeneralizedmotzkinnumbers[J].JIntegerSeq, 2015, 18(4) :Article15.2.4.

(责任编辑邹永红)

Study on the Log-convexity of Colored-Motzkin Numbers

WANG Shan-kun, ZHANG Zhi-hai

(College of urban, Dalian University of Technology, Dalian Liaoning 116600, China)

Abstract:In this paper, by means of constructing Colored-Motzkin triangles array, we verify that the array is the special case of Aigner-Catalan-Riordan arrays. We investigate the log-convexity of Colored-Motzkin numbers by proofing the fact that Colored-Motzkin numbers coincide with the first column of the Colored-Motzkin triangles. For the reason that Catalan numbers, Motzkin numbers and Hexagonal numbers are special cases of Colored-Motzkin numbers, we could get the log-convexity of Catalan numbers, Motzkin numbers and Hexagonal numbers, respectively.

Key words:colored-motzkin numbers；Aigner-Catalan-Riordan arrays；log-convexity

中图分类号：O157.1

文献标志码：A

文章编号：2096-1383(2016)01-0047-03

作者简介：王善坤(1960-)，男，辽宁大连人，副教授，主要从事计算机网络、计算机算法研究。

收稿日期：2015-04-21；最后修回日期：2015-10-08