基于机器学习的学生成绩预警系统建模与研究
2016-02-28吴鲲
吴鲲
(江苏联合职业技术学院扬州商务分院,江苏 扬州 225127)
基于机器学习的学生成绩预警系统建模与研究
吴鲲
(江苏联合职业技术学院扬州商务分院,江苏 扬州 225127)
随着高校智慧校园建设的深入,所采集的校园大数据呈几何基数增长,如何充分利用大数据对校园学习生活进行科学的预测与示警是智慧校园建设研究的重大课题。为了弥补以往的技术不足,采用机器学习技术应用于成绩预警这个领域中,随机森林算法、应用支持向量机(SVM,Support Vector Machine)、线性回归、回归分类树等技术,详细论述了高校学生成绩预警系统的基于机器学习的成绩预警功能的设计与实现。
机器学习;随机森林算法;SVM;成绩预警;智慧校园
高校的智慧校园建设正如火如荼地进行,作为数字化校园的更高级阶段,智慧校园建设强调的是“智慧”,突出的是智能,如何利用大数据技术、云服务、物联网等技术,以人为本地为师生、家长、社会提供信息化服务,以达到为学生的发展和终生幸福打好扎实的基础,是智慧校园建设研究的热点问题。高校学生成绩管理是高校教务系统管理的核心,以往的学生成绩管理系统只关注于学生学习数据的分析,计算不同成绩产生的概率,通过一定的算法推定未来的成绩从而产生预警。这种方法将学生的学习独立于学生的校园活动之外,有其局限性。通过智慧校园产生的大数据,充分采集学生的大数据,如进入图书馆学习的时间、通过门禁进入实训室的时间、校园消费轨迹、网络上网日志等数据,采用随机森林算法建立起高校学生成绩预警系统,以期对学习行为进行警示,全面提高学生的成绩。
一、相关技术综述
(一)决策树
数据的分类以树形结构的方式呈现,每个分支都代表着不同的分类情况。分类的标准分为信息增益法,用信息的增益作为分类划分的标准,如ID3、C4.5算法、基尼指数法。用数据划分的纯度来做比较,最典型的就是CART分类回归树所用的方法,树构造好了之后,可以有剪枝的操作。
(二)随机森林
随机森林算法是用随机的方式来建立一个森林,森林有决策树,每个决策树生成是随机的,它们之间是没有关联的。当有一个新的输入样本进入的时候,就让森林中的每一棵决策树分别进行一下判断,看看这个样本应该属于哪一类(对于分类算法),然后看看哪一类被选择最多,就预测这个样本为那一类。
在传统的CART算法中,每个内部节点都是原始数据集的子集,根节点包含了所有的原始数据而在每个内部节点处,从所有属性中找出最好的分裂方式进行分裂,然后对后续节点依次进行分裂,直到叶子节点最后通过剪枝使测试误差最小。与其他算法不同,随机森林中单棵树的生长可概括为以下几点:
1.使用Bagging方法形成各异的训练集;假设原始训练集中的样本数为N,从中有放回地随机选取个样本形成一个新的训练集,以此生成一棵分类树。
2.随机选择特征对分类回归树的内部节点进行分裂;假设共有M个特征,指定一个正整数m〈〈M,在每个内部节点,从M个特征中随机抽取m个特征作为候选特征,选择这个m特征上最好的分裂方式对节点进行分裂。在整个森林的生长过程中,M的值保持不变。
3.每棵树任其生长,不进行剪枝。
(三)支持向量机(SVM)
支持向量机(SVM)是在统计学习理论和结构风险最小原理基础上发展起来的一种新的机器学习方法,是解决非线性分类、函数估算、密度估算等问题的有效手段,主要思想是建立一个最优决策超平面,使得该平面两侧距平面最近的两类样本之间的距离最大化,从而对分类问题提供良好的泛化能力。根据有限的样本信息在模型中特定训练样本的学习精度和无错误地识别任意样本的能力之间寻求最佳最精确的结果,保证了模型具有全局最优、最大泛化能力、推广能力强等优点,在解决小样本、非线性及高维模式识别中表现出许多特有的优势,并能够推广应用到函数拟合中,能够很好地解决许多实际预测问题。
二、预测模型的建立
(一)关键数据的提取
为了对学生的期末成绩走向有一个合理的预测,根据校园生活实际经验进行了关键词的选取,本文从3个大项、12个小项进行了关键数据的提取,涵盖了学生进入图书馆学习的时间、学生吃饭的时间、学生的课堂学习时间、通过门禁进入实训室的时间、进入机房的时间、校园消费记录、进入宿舍时间、学生上网学习的时间、学生上网游戏的时间、学生上网休闲的时间作为关键数据进行深入的挖掘,所采集的数据是江苏联合职业技术学院扬州商务分院所有学生采集的大数据。
(二)数据特征值的提取

表1 关键数据表
特征的选取对于构建决策树的分类十分重要,提取出合适的特征值对于预测学生成绩发展的趋势具有十分重要的意义。在选择特征值时,希望发现那些对学生成绩波动影响特别大的特征集。
决策树(随机森林)的特征值的选取依赖于已知数据,利用决策树我们对测试集进行分类,以此判断是否需要对学生进行预警。在这个过程中,由于树的划分太细,很容易造成过拟合的问题。在这里,我们可以利用剪枝来确认最终的特征值,剪枝的方法主要有如下几种:(1)错误率降低剪枝:最简单的剪枝方法,减少某个节点看是否能够提高正确率(利用训练集来验证正确率而不是测试集)。(2)悲观剪枝:主要依据概率论根据自身节点比较信息增益来进行剪枝。(3)代价复杂度:主要是通过增加新的节点看是否能大幅提升准确率,通过阈值来判断是否增加新的节点)。随机森林的本质就是多棵决策树的组合,利用不怎么准确的决策方法生成最终一个可靠的结果。
三、基于随机森林的学习成绩预测算法
(一)模型的算法
首先我们得到决策树,下面我们就需要进行相对应的剪枝。这里我们利用剪枝前后信息熵的变化来说明。以属性R分裂前后的信息增益比其他属性最大。这里信息的定义如下:

其中的m表示数据集D中类别C的个数,Pi表示D中任意一个记录属于Ci的概率,计算时Pi=(D中属于Ci类的集合的记录个数/|D|)。Info(D)表示将数据集D不同的类分开需要的信息量。
熵表示的是不确定度的度量,如果某个数据集的类别的不确定程度越高,则其熵就越大。比如我们将学生上网浏览的目的定义为f1,f1的取值为{1,2,3,4,5,6},代表有六种不同的可能性,则f1的熵entropy(f1)=-(1/6*log (1/6)+…+1/6*log(1/6))=-1*log(1/6)=2.58;我们将学生进入图书馆的目的定义为f2,f2的取值为 {1,2,3,4},f2的熵entropy(1)=-(1/4*log(1/4)+1/4*log(1/4)+1/4*log(1/4) +1/4*log(1/4)) =-log(1/4)=2;将学生进入实训室的目的定义为f3,显然学生进入实训室一定是为了学习,即f3的取值为{1},故其熵entropy(f3)=-1*log(1)=0。可以看到,可能的情况越多,熵值也越大。而当只有一个可能时,熵值为0,此时表示不确定程度为0,也就是学生的目的是确定的。
有了上面关于熵的运算,我们接着计算信息增益。假设我们选择属性R作为分裂属性,数据集D中,R有k个不同的取值{V1,V2,…,Vk},于是可将D根据R的值分成k组{D1,D2,…,Dk},按R进行分裂后,将数据集D不同的类分开还需要的信息量为:

信息增益的定义为分裂前后,两个信息量只差:

信息增益Gain(R)表示属性R给分类带来的信息量,我们寻找Gain最大的属性,就能使分类尽可能的纯,即最可能地把不同的类分开。不过我们发现,对所有的属性Info(D)都是一样的,所以求最大的Gain可以转化为求最新的。
(二)实际预测过程
下面这个例子会预测学生是否沉迷于网络,首先我们得到如此的决策树,下面就需要进行相对应的剪枝。因为不同年级的课余时间不一样,我们将年级作为一个特征值,学生到课率作为第二个特征值,学生上网日志访问游戏类网站地址的频率作为第三个特征值;将学生上网频率作为第四个特征值。数据集D如附表1:

图1 决策树
附表1的数据集是根据学生的年级、上网频率、是否经常访问游戏IP以及到课率来确定他是否会沉迷于网络,即最后一列“是否沉迷于网络”是类标。现在我们用信息增益选出最佳的分类属性,计算按年级分裂后的信息量:
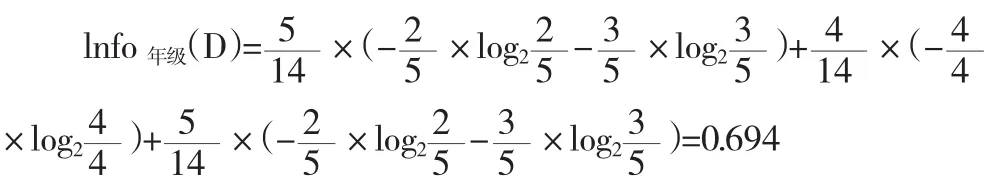
整个式子由三项累加而成,第一项为一年级,14条记录中有5条为一年级,其中2(占2/5)条沉迷于网络,3(占3/5)条不沉迷于网络。第二项为二年级,第三项为三年级。类似的有:

同理,得出:lnfo访问游戏(D)=0.789 ,lnfo到课率(D)=0.892
可以得出lnfo年级(D)最小,说明不要增加信用等级这个节点,增加之后不确定新增加,即以年级分裂后,分得的结果中类标最纯,此时以年级作为根结点的测试属性。
由于数据来源不同,存在不同的结果结合。这里首先根据随机森林得到相对应的分类。然后进行剪枝,得到相对应的特征,再利用这些特征对结果进行分类,同时我们把这个随机森林方法应用到历史的情况,利用提取学生的一卡通、门禁等各种数据以及SVM方法来拟合某学期成绩的升降(采用交叉检验,使得结果具有稳定性不至于出现过拟合的问题)。利用这个拟合函数来预测学生本学期的分差,而如果结果的趋势和Tree的判别趋势相同我们就选择采信这种方法,如果两个结果趋势矛盾,我们将利用这个学生本人的历史数据再次进行SVM模拟,将结果加入到之前的SVM模型当中。
用SVM方法来拟合历史上特征量的变化和最终分差的差别,利用这个SVM拟合来拟合本学习期学生的变化得到最终的分差。这里的分差表示学生本学期均分和以往均分的变化,正值表示学生成绩下滑,负值表示学生成绩上升。因此,我们就可以在学期中通过这种算法不断提醒某些学生可能存在成绩下滑的危险或大幅度上升的趋势。
四、预测结果与分析
(一)预测结果
完成对模型建模与计算后,分别对学校一年级、二年级、三年级的学生数据进行分类与拟合,计算最终分差,这里截取了部分同学的分差,如表2,并形成年级成绩分差趋势图,如图2。
(二)结果分析
如图3所示,我们将2015年学校三个年级成绩趋势分差的预测值和学校三个年级实际成绩分差进行了对比,模型拟合效果总体成绩趋势较为理想,但预测分差值和实际分差值浮动的幅度还是较大,需要在以后的研究中再引入其他数据加以改进。

表2 各年级学生成绩分差
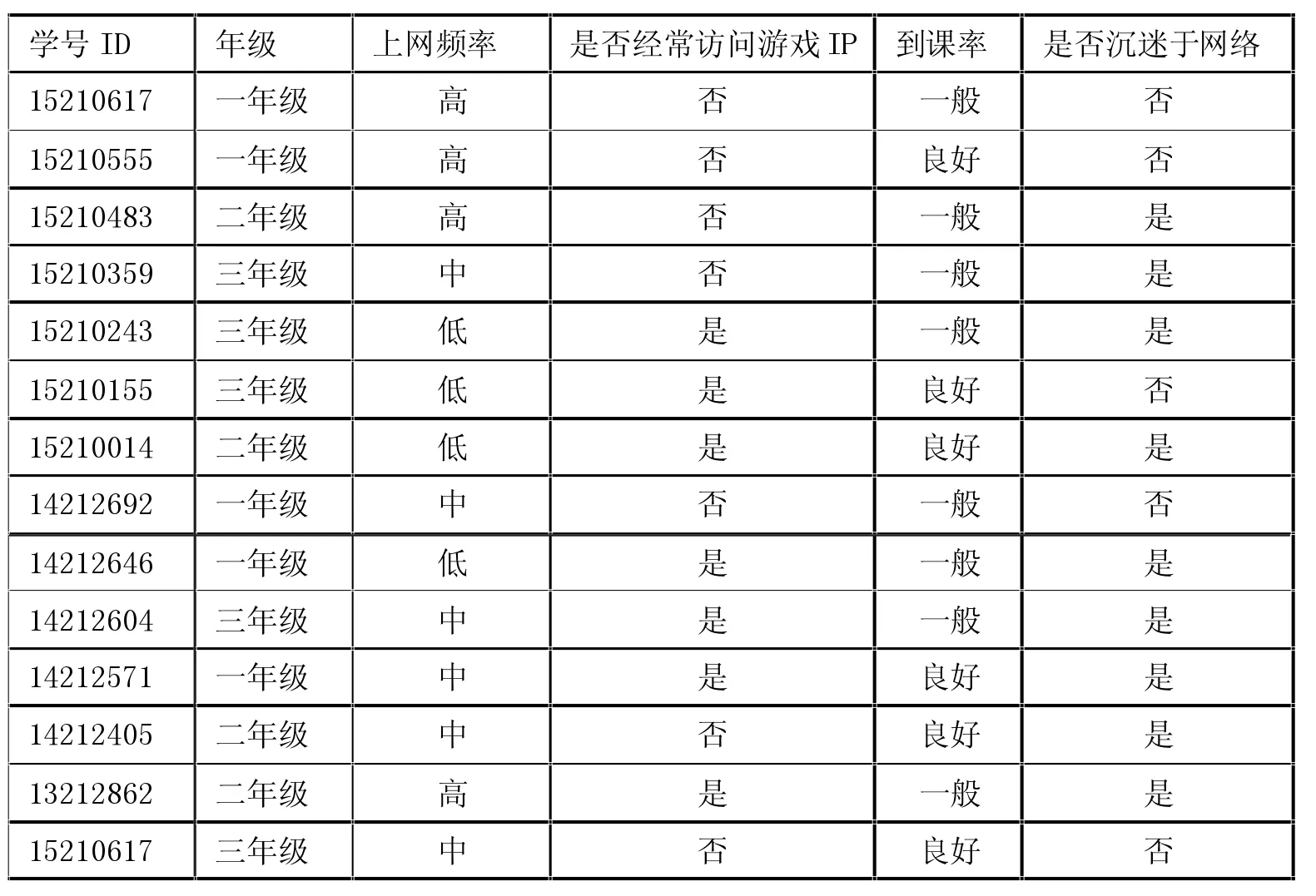
附表1 学生上网数据统计

图2 各年级学生成绩分差趋势

图3 预测成绩与实际对比图
[1]Brett Lanta.机器学习与R语言[M].北京:机械工业出版社,2015:5-17.
[2]方匡南,吴见彬,朱建平,谢邦昌.随机森林方法研究综述[J].统计与信息坛,2011(3):32-38.
[3]董师师,黄哲学.随机森林理论浅析[J].集成技术,2013(1):1-7.
[4]刘华煜.基于支持向量机的机器学习研究[D].大庆石油学院,2005.
[5]王全才.随机森林特征选择[D].大连理工大学,2011.
TP
A
1673-0046(2016)12-0178-03
