加性乘性噪声改善多元信号检测
2016-02-27王友国
王友国,潘 慧,刘 健
(1.江苏省物联网技术与应用协同创新中心,江苏 南京 210003;2.南京邮电大学 通信与信息工程学院,江苏 南京 210003)
加性乘性噪声改善多元信号检测
王友国1,2,潘 慧2,刘 健2
(1.江苏省物联网技术与应用协同创新中心,江苏 南京 210003;2.南京邮电大学 通信与信息工程学院,江苏 南京 210003)
基于最大后验概率准则,以错误检测概率为测度,研究了加性噪声和乘性噪声共同作用下信号检测的问题。在乘性噪声强度不变的情况下,当信号是阈上时,错误检测概率随着加性高斯噪声强度的增加而单调增加,噪声总是干扰信号检测;当信号是阈下时,错误检测概率随着加性高斯噪声强度的增加而逐渐降低至一个最小值后再缓慢增加,适量的噪声有利于多元信号检测,即随机共振存在。在加性高斯噪声强度不变的情况下,当信号是阈上时,错误检测概率随着乘性噪声强度的增加而单调增加,噪声总是恶化信号检测性能;当信号是阈下时,错误检测概率随着乘性噪声强度的增加而单调下降并最终趋于稳定。这些结论有助于噪声改善多元信号检测。
随机共振;多元信号检测;错误检测概率;乘性噪声
0 引 言
噪声广泛存在于通信系统中,对信号的传输与处理造成干扰。传统的观点认为噪声总是恶化信号的传输,于是研究者们探求各种去噪、滤波方法来减小噪声的影响,提高信号的接收功效。然而在某些非线性系统中,如果系统、噪声和信号三者之间达到某种匹配关系,那么噪声的能量可以向信号转移,从而对信号的检测起到积极作用。这种噪声改善信息传输和信号处理的现象称为随机共振(Stochastic Resonance,SR),是由Benzi等在解释远古气象学中冰川期与暖气候期周期性交替出现的现象时首次提出的[1]。目前,SR的研究已经涉及许多领域[2-7]。
二元信号检测中的随机共振研究已经有了许多成果[8-14],文献[8]利用外加高斯噪声提高信号检测概率,文献[14]在聂曼-皮尔逊(NP)准则下,利用两个常值噪声的组合,得到最佳的信号检测概率。在实际中,噪声的分布类型是多样的,并且会以加性和乘性的形式共同作用于信号上[15-18]。文中考虑加性与乘性噪声共同作用下的信号检测功效,其中乘性噪声选用四种典型分布的噪声[19-20],而加性噪声设定为高斯噪声。基于最大后验概率(MAP)准则,文中利用非线性求和统计量,对接收信号进行判决检测,推导出噪声作用下的信号检测错误概率,并探讨噪声改善多元信号检测的功效。
1 多元信号检测
以三元信号为例,讨论加性乘性噪声改善信号检测的情况。取s为三元信号,在假设H-1,H0,H1下分别取为-1,0,1,相应的先验概率为p-1,p0,p1(p-1+p0+p1=1)。含噪信号x=s+sξ+η,通过一个非线性阈值系统,得到输出信号为:
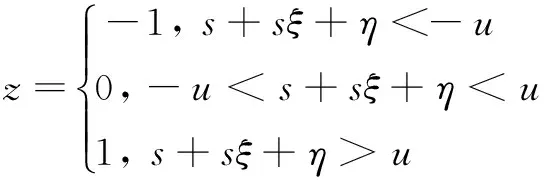
(1)
其中,ξ为乘性噪声;η为加性噪声;u为系统阈值且是可调节的。
由MAP准则可得求和统计量zs的似然比[19]为:
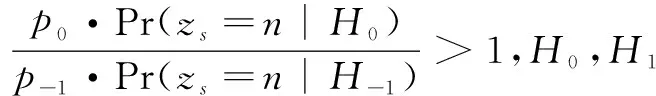

(2)

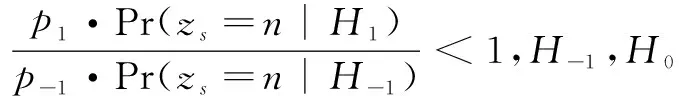
(3)
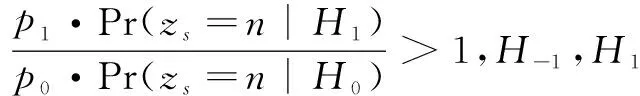

(4)
于是信号检测的最小错误概率为:
学校成立由主要领导担任负责人的创新创业教育指导委员会,负责创新创业的指导、孵化、实践和培育。创指委的具体事务包括协调学校双创教育的教学改革、课程建设、师资培养、项目管理、竞赛组织、基地建设、学生活动和咨询服务等,制定双创教育的实施规范或评价标准,组织创新创业师资培训、学术研讨和信息交流等工作。
2 加性与乘性噪声形式
2.1 加性噪声
通信与信号处理中,加性高斯白噪声是一种普遍考虑并得到广泛研究的噪声。对于式(1)中的加性噪声η,文中同样选取为零均值的高斯噪声,概率密度函数为:
(6)
2.2 乘性噪声
乘性噪声与信号相关,在不同的环境下具有不同的形式。基于文献[20],文中考虑乘性噪声分别呈现为均匀分布、高斯分布、拉普拉斯分布以及柯西分布的情况,展示不同环境中不同类型乘性噪声的功效。
均值为零、标准差为σ的均匀噪声的概率密度函数为:
(7)
其对应的分布函数为:
(9)
其对应的分布函数为:
均值为零、标准差为σ的拉普拉斯噪声的概率密度函数为:
(11)
其对应的分布函数为:
具有零位置,标准离差为σ的柯西噪声的概率密度函数为:
(13)
其对应的分布函数为:
2.3 最小错误概率
对于2.1节与2.2节给出的加性噪声η和乘性噪声ξ,概率密度函数分别为fη(η)和fξ(ξ),累积分布函数分别为Fη(·)和Fξ(·),可以得到以下条件概率。
Pr(zi=-1|Hs)=Pr(s+s·ξ+η<-u)=
(15)
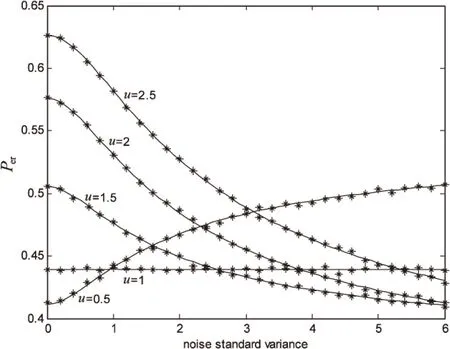
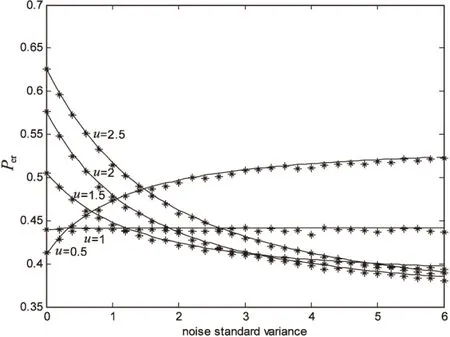
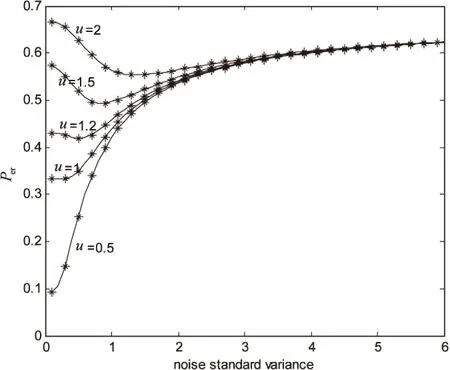
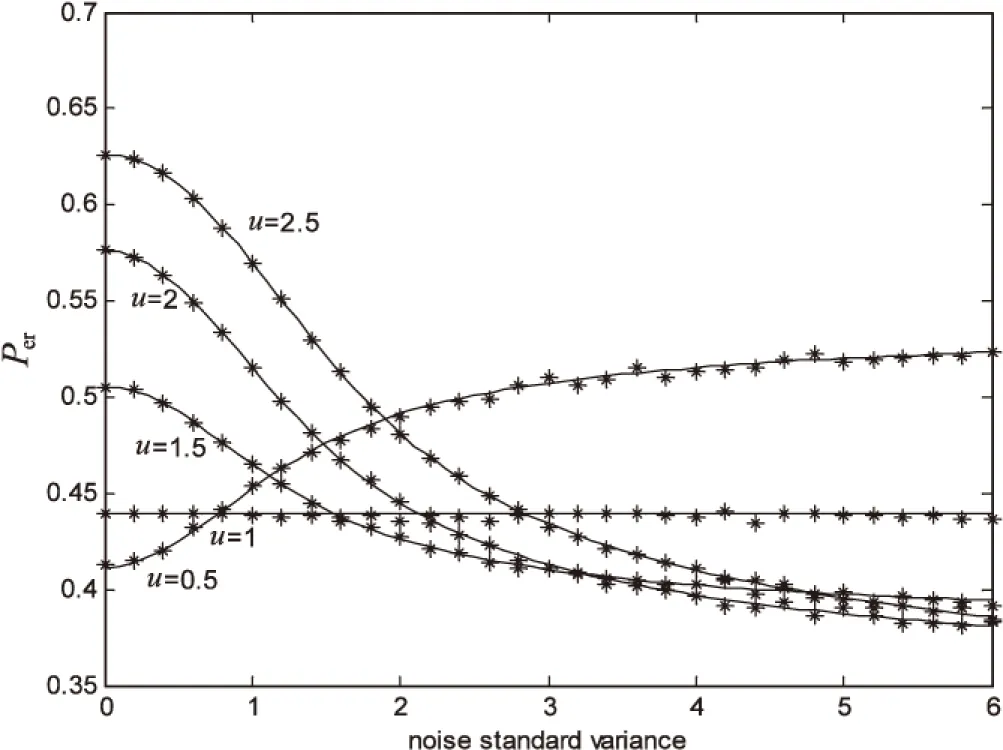
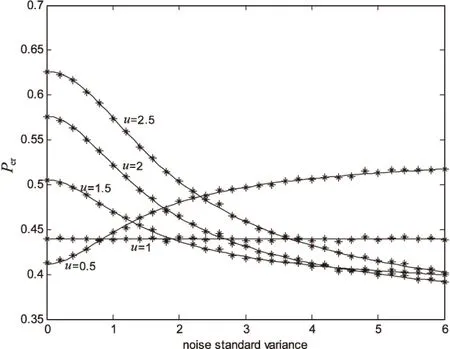
Pr(zi=0|Hs)=Pr(-u (16) Pr(zi=1|Hs)=Pr(s+s·ξ+η>u)= (17) 其中,qj,s=Pr(z=j|Hs),j,s=-1,0,1。 图1 乘性均匀噪声强度为0.4时,在不同阈值水平下Per随加性高斯噪声强度变化的曲线图 由图可知,仿真结果与理论结果相吻合。当输入信号为阈上信号(u≤1)时,Per随加性噪声强度的增加而单调增加,即信号检测性能随着加性噪声强度的增加而衰减;而当输入信号是阈下信号(u>1)时,错误概率曲线呈下凸形状,存在最优的加性噪声强度,使得Per达到最小值,即发生随机共振现象。可见,适量的加性噪声有利于提高多元信号的检测性能,这与文献[19]中的结论相一致。此外,从图1~4可以看出,噪声强度较小时,错误概率处于较高水平值,这是因为噪声过弱无法辅助信号越过阈值门限,对检测性能的改善效果不明显。而噪声强度较大时,不同阈值下的错误概率近似相等,这是由于过强的噪声诱导了系统线性化[11]。 图2 乘性高斯噪声强度为0.4时,在不同阈值水平下Per随加性高斯噪声强度变化的曲线图 图3 乘性拉普拉斯噪声强度为0.4时,在不同阈值水平下Per随加性高斯噪声强度变化的曲线图 图4 乘性柯西噪声强度为0.4时,在不同阈值水平下Per随加性高斯噪声强度变化的曲线图 在加性高斯噪声强度固定的情况下,图5~8给出了乘性噪声分别为四种经典噪声时,在不同阈值水平下错误检测概率随乘性噪声强度变化的理论线和蒙特卡洛数据仿真点。由图可知,仿真结果与理论结果相吻合。当输入信号为阈上信号(u≤1)时,乘性噪声总是恶化信号检测性能,此时不会产生随机共振现象。而当输入信号是阈下信号(u>1)时,错误检测概率随乘性噪声强度的增加而单调下降,随机共振现象发生。同时,过强的乘性噪声不会提高信号检测的错误概率,而是使得错误概率降低并趋于一个稳定值。这是因为乘性噪声作用于信号上,乘性噪声强度增强可以等效为信号能量的增大,从而使得多元信号的检测更加可靠。这些结果显示了乘性噪声在多元信号检测中的功效。 图5 加性高斯噪声强度为1时,在不同阈值水平下Per随乘性均匀噪声强度变化的曲线图 图6 加性高斯噪声强度为1时,在不同阈值水平下Per随乘性高斯噪声强度变化的曲线图 基于最大后验概率准则,文中研究了加性高斯噪声和四种乘性噪声共同作用下三元信号检测的问题。类似于加性噪声单独作用时得到的随机共振功效,当信号为阈下时,加性噪声与乘性噪声共同作用时信号错误检测概率降低,信号检测的性能得到改善,产生随机共振现象。当信号为阈上时,乘性噪声和加性噪声都恶化系统检测性能,阈值的恰当选取对随机共振现象的产生至关重要。这些结论拓展了随机共振在多元信号处理中的应用。 图7 加性高斯噪声强度为1时,在不同阈值水平下Per随乘性拉普拉斯噪声强度变化的曲线图 图8 加性高斯噪声强度为1时,在不同阈值水平下Per随乘性柯西噪声强度变化的曲线图 [1]BenziR,SuteraA,VulpianiA.Themechanismofstochasticresonance[J].JournalofPhysicsA:MathematicalandGeneral,1981,14(11):453-457. [2]McNamaraB,WiesenfeldK.Theoryofstochasticresonance[J].PhysicalReviewA,1989,39(9):4854-4869. [3]DuanF,Chapeau-BlondeauF,AbbottD.Encodingefficiencyofsuprathresholdstochasticresonanceonstimulus-specificinformation[J].PhysicsLettersA,2016,380(1-2):33-39. [4]DuanF,Chapeau-BlondeauF,AbbottD.Non-Gaussiannoisebenefitsforcoherentdetectionofnarrowbandweaksignal[J].PhysicsLettersA,2014,378(26-27):1820-1824. [5]LiQ,LiZ.Anovelsequentialspectrumsensingmethodincognitiveradiousingsuprathresholdstochasticresonance[J].IEEETransactionsonVehicularTechnology,2014,63(4):1717-1725. [6]GuoY,TanJ.EffectsofGaussiancolorednoiseontimeevolutionofinformationentropyinadampedharmonicoscillator[J].PhysicaA:StatisticalMechanicsandItsApplications,2015,419:691-697. [7] 翟其清,王友国,郑 克.噪声改善码元传输[J].计算机技术与发展,2014,24(11):152-154. [8]KayS.Candetectabilitybeimprovedbyaddingnoise?[J].IEEESignalProcessingLetters,2000,7(1):8-10. [9]WangY,WuL.Nonlinearsignaldetectionfromanarrayofthresholddevicesfornon-Gaussiannoise[J].DigitalSignalProcessing,2007,17(1):76-89. [10]Chapeau-BlondeauF,RousseauD.Constructiveactionofadditivenoiseinoptimaldetection[J].InternationalJournalofBifurcationandChaos,2005,15(9):2985-2994. [11]WangY.NonlinearstatisticstoimprovesignaldetectioningeneralizedGaussiannoise[J].DigitalSignalProcessing,2008,18(3):444-449. [12]GuoG,MandalM,JingY.Arobustdetectorofknownsignalinnon-Gaussiannoiseusingthresholdsystems[J].SignalProcessing,2012,92(11):2676-2688. [13]Chapeau-BlondeauF.Nonlinearteststatistictoimprovesignaldetectioninnon-Gaussiannoise[J].IEEESignalProcessingLetters,2000,7(7):205-207. [14]ChenH,VarshneyPK,KayS,etal.Theoryofthestochasticresonanceeffectinsignaldetection:partI-Fixeddetectors[J].IEEETransactionsonSignalProcessing,2007,55(7):3172-3184. [15]MitaimS,KoskoB.Adaptivestochasticresonance[J].ProceedingoftheIEEE,1998,86(11):2152-2183. [16] 罗鹏飞.统计信号处理[M].北京:电子工业出版社,2009. [17]JiaY,YuS,LiJ.Stochasticresonanceinabistablesystemsubjecttomultiplicativeandadditivenoise[J].PhysicalReviewE,2000,62:1869-1878. [18]JiangX,WangF,YanX.Stochasticresonanceinbistablesystemsubjecttomultiplicativeandadditivenoise[J].SemiconductorPhotonics&Technology,2010,4:156-161. [19]WangY,HuQ.Stochasticresonanceinnonlinearmultiplesignaldetectionforfourrepresentativenoises[J].LectureNotesinElectricalEngineering,AdvancesinComputer,Communication,ControlandAutomation,2011,121:607-616. [20]LiuJ,WangY,ZhaiQ.Stochasticresonanceofsignaldetectioninmono-thresholdsystemusingadditiveandmultiplicativenoises[J].IEICETransactionsonFundamentalsofElectronics,CommunicationsandComputerSciences,2016,99(1):323-329. Improvement of Multiple Signal Detection by Additive and Multiplicative Noise WANG You-guo1,2,PAN Hui2,LIU Jian2 (1.Jiangsu Innovative Coordination Center of Internet of Things,Nanjing 210003,China; 2.College of Communication and Information Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China) Stochastic Resonance (SR) is discussed in nonlinear multiple signal detection for additive noise and multiplicative noise based on the Maximum Posterior Probability (MAP) criterion in the probability of detection error measure.In the case that multiplicative noise intensity is fixed,when the signal is suprathreshold,the probability of detection error increases monotonously with the additive Gaussian noise intensity and noise always interfere signal detection;when the signal is subthreshold,with the increase of additive Gaussian noise intensity,the probability of detection error gradually reduces to a minimum value and then increases slowly and the noise can improve the signal detection,i.e.,SR exists.In the case that additive noise intensity is fixed,when the signal is suprathreshold,the probability of detection error increases monotonously with the multiplicative noise intensity which indicates that noise is always deteriorate signal detection performance;when the signal is subthreshold,the probability of detection error decreases monotonously and finally tends to a steady value with the increasing of multiplicative noise intensity.These conclusions can be able to be helpful for noise improving multiple signal detection. stochastic resonance;multiple signal detection;probability of detection error;multiplicative noise 2015-12-21 2016-04-05 时间:2016-09-19 国家自然科学基金资助项目(61179027);江苏省“青蓝工程”基金(QL06212006);江苏省高校研究生科研创新计划项目(KYLX15_0831) 王友国(1968-),男,教授,研究方向为信号与信息处理;潘 慧(1990-),女,硕士研究生,研究方向为信号与信息处理。 http://www.cnki.net/kcms/detail/61.1450.TP.20160919.0839.008.html TP39 A 1673-629X(2016)10-0160-05 10.3969/j.issn.1673-629X.2016.10.035
3 实验仿真及随机共振现象
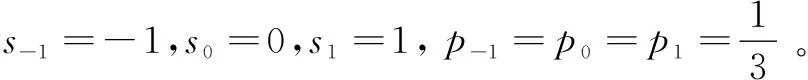



4 结束语