基于矩阵自定义运算的Floyd改进算法

赵礼峰，黄奕雯

(南京邮电大学 理学院，江苏 南京 210046)

基于矩阵自定义运算的Floyd改进算法

赵礼峰，黄奕雯

(南京邮电大学 理学院，江苏 南京 210046)

解决最短路问题的算法层出不穷，其中最经典的要数Dijkstra算法和Floyd算法。但Dijkstra算法只能得出一对节点间的最短距离，而Floyd算法计算过程十分繁琐。为解决这两种经典算法中的缺陷，提出一种基于矩阵自定义运算的Floyd改进算法。该算法通过自定义矩阵运算得出一个表示两两节点间距离的路权修正矩阵，再用路权修正矩阵与原距离矩阵进行比较，选择两矩阵中对应较小元素组成当前最短路权矩阵，再通过有限次的迭代，从而得到各顶点间的最短路。通过MATLAB仿真，将该算法推广到随机大规模复杂网络中，通过运行时间折线图表明，该算法在节点达到一定数量后运行速度明显优于传统算法，且在稀疏网络中运行效率非常高，说明了该算法的有效性。最后，通过具体应用说明了该算法的实用性。

最短路问题;Floyd算法;矩阵自定义运算;MATLAB;稀疏网络

0 引 言

随着社会的发展，最短路问题在日常生活中的应用越来越广泛，小到上班上学走哪条路最近，大到网络路由以及基站的选址，还有交通旅行、城市规划、电网架设，最短路问题出现在生活的方方面面。如果掌握了最短路算法，那么可以给生活带来许多便利。为了解决简单的最短路问题，提出了许多简便的算法，如Dijkstra算法、Floyd算法、Kruskal算法、拓扑排序法、启发式搜索算法、A*算法、动态规划算法以及神经网络遗传算法等等[1-6]。然而Dijkstra算法和Floyd算法无法解决任意顶点间最短路长的问题，而且Floyd算法十分繁琐。

针对上述问题，文中提出了一种基于矩阵自定义运算的Floyd改进算法。该算法在计算权矩阵时直接在权值旁对路径进行标注，省去了路径矩阵的求解。同时，在运算过程中对矩阵元素出现∞时不进行运算，大大简化了运算量。特别是在稀疏矩阵中，由于稀疏矩阵中有大量的∞元素，那么只需计算其中几个非∞元素，算法优势显而易见。但是当阶数n非常大时，计算依然十分复杂，所以需要借助计算机用计算机语言来实现大型网络的计算。文中借助MATLAB实现该算法。

1 相关知识

定义1[7]赋权图：设G=(V,E)为一幅图，给G的每一条边e赋予一个权值w(e),w(e)可以指网络流量、运输费用、物理距离、消耗时间等。若图G的所有边都赋予权值，称G为赋权图或网络。

定义2[7]最短路径：在带权图G=(V,E)中，若顶点vi，vj是图G的两个顶点，从顶点vi到vj的路径长度定义为路径上各条边的权值之和。从顶点vi到vj可能有多条路径，其中路径长度最小的一条称为顶点vi到vj的最短路径。

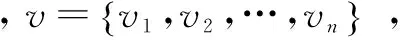
定义4[3]稀疏网络：用稀疏矩阵存储的网络。

定义5、定义6是文中给出的：

定义5 稀疏矩阵：包含大量0元素的矩阵，在最短路问题中，可以认为含有大量∞元素的矩阵。

定义6 矩阵自定义运算⊕：现定义一种运算⊕，使得：

那么有：

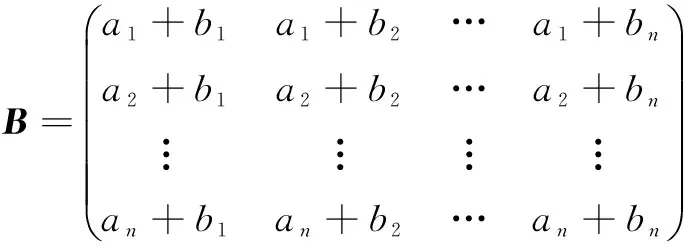
这种新定义的运算相当于连接两条经过统一定点的路径。每做一次⊕运算相当于原路径经过一次中间节点。

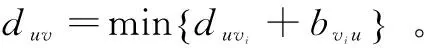
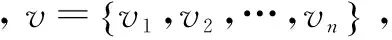
(1)

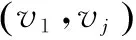
2 基于矩阵自定义运算的Floyd改进算法

2.1 算法思想

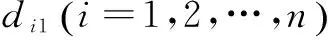
与此同时，以标注法直接在代表距离的权值旁的括号中标注路径。当插入某个节点vk后，若计算出的最短路径长度小于原来不经过vk时的长度，那么就将该节点的下标k直接标注在权矩阵中对应的元素的右边括号中表明vk为最短路中路过节点，若路过节点不止一个则依次标明。

最后，当加法运算中一个加法项dij出现∞时，不用计算，直接得∞；当加法项dij出现0时，同样无需计算，直接写上另一个加法项，从而简化计算。

2.2 算法步骤

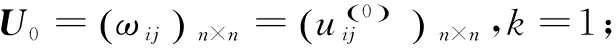
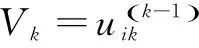
Step2:如果k=n，结束；否则，令k:=k+1,转Step1。

2.3 算法复杂度分析

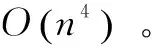
3 算 例

以图1为例，得出各个顶点间的最短路。

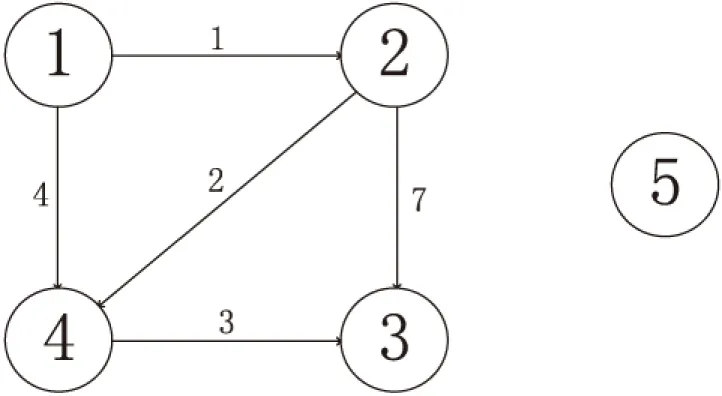
图1 稀疏网络

所以，经过V2和U0的比较，有

所以，经过V4和U2的比较，有

由于最后一行不用计算，所以U5=U4即为最终得出的结果。

4 算法的仿真与可行性分析

利用MATLAB[10]对文中提出的算法进行仿真。首先运行普通网络，接着运行稀疏网络，同时与传统算法的运行作对比，通过运行时间的长短说明该算法的优越性。由仿真结果可知，该算法可以推广到大规模随机复杂网络中，进一步说明了该算法的实用性。

由于是随机生成的网络，每次的运行结果有所差别，所以对它的运行时间取一个平均值。表1为对10阶，20阶，直到100阶矩阵运行20次取得的平均结果，将它的运行时间与传统Floyd算法进行比较。图2为该改进算法与传统算法运行时间相比的折线图。

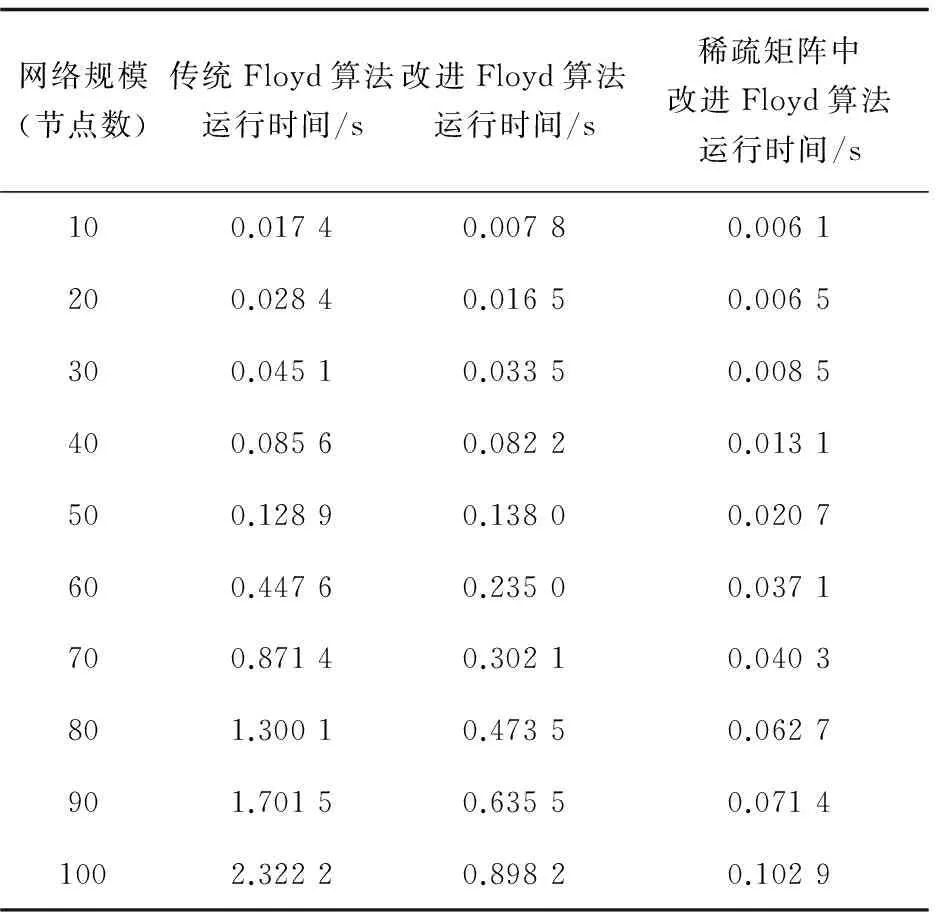
表1 算法运行时间

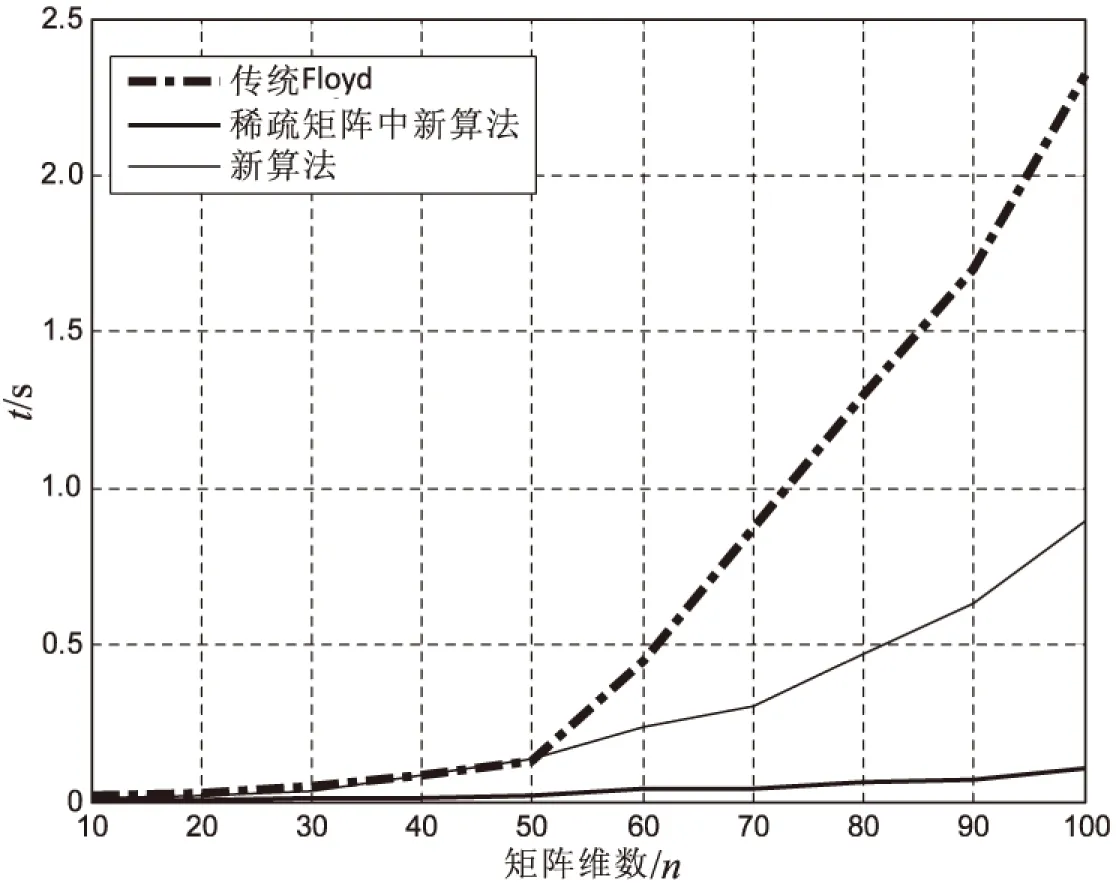
图2 算法运行时间对比折线图

5 实际应用举例

最短路问题的应用非常广泛,举一个实际生活中存在的旅游班车选乘问题[11-14]的例子来说明最短路问题在生活中的应用。

例：南京旅游局开通了一条旅行专线,途中经过5个景点(奥体中心(A)、夫子庙(B)、中华门(C)、玄武湖(D)、中山陵(E))，每班车的发车时间固定(见表2)。如果在某一时刻出发从一个景点到另一个景点,讨论不同时刻出发去某一景点的最短时间。(将路途中经过的时间看作是路的权值,那么，求最短时间的问题就可以看作是求最短路问题,即可以用文中求最短路的方法来解决。)

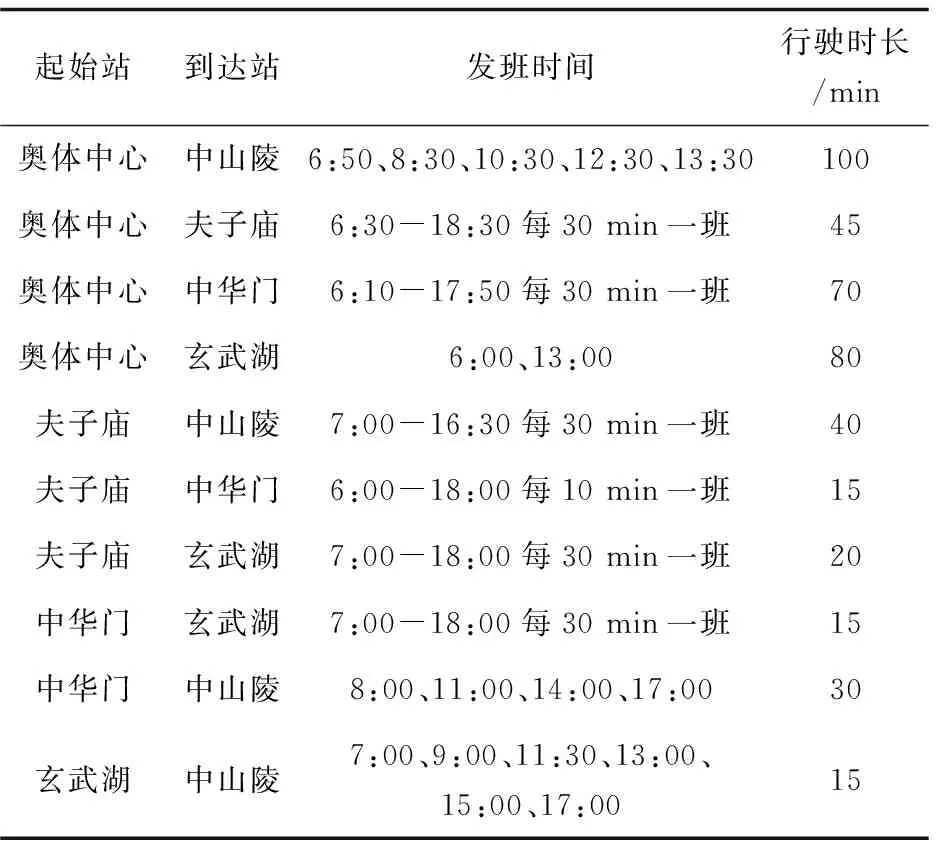
表2 班车时刻表

问：某人在11:30要从奥体中心出发去中山陵游玩，怎样乘车才能最快到达？

解：把换乘旅行班车问题运用到图论中转化为最短路问题。首先，令奥体中心为A点(在本例中作为发点)，中山陵作为E点(在本例中作为收点)，做出旅行班车的路线图，因为旅行班车停靠点时间固定，所以不同的出发时间，会有不同的时间图，即图中边上的权值不同。图3为11:30时出发的路线图，为赋权无回路有向图。

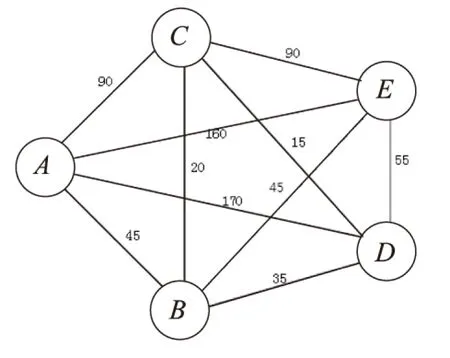
图3 景点分布图

初始矩阵为：

用以上算法求解最终得到：

由于最后一行不用计算，所以U5=U4即为最终得出的结果。

即，从奥体中心(A)到中山陵(E)最快需要90min，行驶路线为：奥体中心(A)→夫子庙(B)→中山陵(E)。

6 结束语

通过应用实例可以看出该算法在实际运用中的作用；经过程序测试，算法能够得到任意节点间最短路。由仿真结果可以看出，当网络节点较小时，该算法在一般网络中与传统算法相比，运行时间并没有得到明显提高；但是，当节点增多到50个以上时，该算法明显快于传统算法。同时，在稀疏网络中，无论从时间复杂度，还是空间复杂度来说，文中算法优越性明显。

[1] 张德全,吴果林,刘登峰.最短路问题的Floyd加速算法与优化[J].计算机工程与应用,2009,45(17):41-43.

[2] 张德全,吴果林.最短路问题的Floyd算法优化[J].许昌学院学报,2009,28(2):10-13.

[3] 吴果林,金 珍,邓小方.稀疏网络的Floyd动态优化算法[J].江西师范大学学报:自然科学版,2013,37(1):28-32.

[4] 邓方安,雍龙泉,周 涛,等.基于“矩阵乘法”的网络最短路径算法[J].电子学报,2009,37(7):1594-1598.

[5] 赵礼峰,梁 娟.最短路问题的Floyd改进算法[J].计算机技术与发展,2014,24(8):31-34.

[6] 邹桂芳,张培爱.网络优化中最短路问题的改进Floyd算法[J].科学技术与工程,2011,11(28):6875-6878.

[7] 谢 政.网络算法与复杂性理论[M].长沙:国防科技大学出版社,2003.

[8] 刘焕淋,陈 勇.通信网图论及应用[M].北京:人民邮电出版社,2010.

[9] Hougardy S. The Floyd-warshall algorithm on graphs with negative cycles[J].Information Processing Letters，2010,110:279-281.

[10] 刘卫国.MATLAB程序设计与应用[M].北京:高等教育出版社,2006.

[11] 李 科,袁 明.小件快运中的最短运输时间问题[J].山东交通科技,2011(5):23-25.

[12] Feillet D,Dejax P,Gendreau M.Traveling salesman problems with profits[J].Transportation Science,2005,39(2):188-205.

[13] Braess D,Nagurney A,Wakolbinger T.On a paradox of traffic planning[J].Transportation Science,2005,39(4):446-450.

[14] Zhan F B.Three fastest shortest path algorithms on real road networks[J].Journal of Geographic Information and Decision Analysis,1997,1(1):69-82.

Improved Floyd Algorithm Based on Customized Matrix Operations

ZHAO Li-feng,HUANG Yi-wen

(College of Mathematics and Physics,Nanjing University of Posts and Telecommunications,Nanjing 210046,China)

The algorithm to solve the shortest path problem is endless,and the algorithm of Dijkstra and Floyd is the most typical.However,the Dijkstra algorithm can only get the shortest distance between a pair of nodes,and Floyd algorithm is very cumbersome.For solving their defects in two classical algorithms,an improved Floyd algorithm is proposed based on matrix custom operation.It obtains a modified matrix between two nodes by using a customized matrix calculation,and then compares the modified matrix with the original distance matrix,selecting the smaller matrix elements for composition of the shortest path weight matrix.Through finite iteration,the shortest path is obtained between each vertex.By the MATLAB simulation,the algorithm is extended to stochastic large-scale complex networks.The running time line chart shows that this algorithm runs faster than traditional algorithm after a certain number of nodes,and in sparse network,the efficiency is particularly high,which shows the its effectiveness.Finally,by using the specific application,the feasibility of the algorithm is verified.

shortest path problem;Floyd algorithm;matrix custom operations;MATLAB;sparse network

2015-11-23

2016-03-03

时间：2016-08-01

国家自然科学基金资助项目(61304169)

赵礼峰(1959-),男,教授,硕士研究生导师,研究方向为图论及其在通信中的应用;黄奕雯(1991-),女,硕士研究生,研究方向为图论及其在通信中的应用。

http://www.cnki.net/kcms/detail/61.1450.TP.20160801.0904.024.html

TP301.6

A

1673-629X(2016)10-0041-04

10.3969/j.issn.1673-629X.2016.10.009