求解k最短路径问题的混合遗传算法

赵礼峰，于汶雨

(南京邮电大学 理学院，江苏 南京 210023)

求解k最短路径问题的混合遗传算法

赵礼峰，于汶雨

(南京邮电大学 理学院，江苏 南京 210023)

遗传算法求解问题的关键在于对问题的解进行编码,同时需要构造出适应度函数。结合k最短路径实际问题，重新定义了一种染色体编码方式，并且新构造了符合该问题的适应度函数。标准遗传算法采用固定的交叉率和变异率,在应用过程中存在收敛过慢、早熟及稳定性差的缺点。因此，提出了一种改进的自适应遗传算法,对交叉率和变异率采用自适应方式,构造了确定交叉率和变异率的公式，加快了算法收敛速度。同时结合模拟退火的Metropolis准则对子代个体的接收做出选择，克服了算法容易早熟的问题。仿真结果表明，改进后的混合遗传算法可以求解k最短路问题，并且在寻优精确度、时间效率、稳定性上均优于标准遗传算法。

混合遗传算法；染色体编码；Metropolis准则；k最短路径

0 引 言

k最短路问题[1]是图论中研究的一个重要课题，同时在现代计算机网络以及交通系统中扮演着重要的角色。该问题最早由Hoffman和Pavley在20世纪50年代提出[2]，多年来也一直受到学术界的广泛关注，并且先后提出了多种求解k最短路径问题的算法。因此，如何快速求解k最短路径问题成为了研究的重点。文献[3]主要的研究成果是基于Dijkstra算法的前N条最短路径算法；文献[4-6]利用“偏离路径”的性质给出计算k条最短路径的递推公式,但在求解第k条最短路径时采用了不同的方法。

遗传算法(Genetic Algorithm)[7]是由美国J.Holland教授在1975年首先提出的、模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程演化而来的随机化搜索方法。近年来在世界范围内形成进化计算热潮，计算智能已成为人工智能研究的一个重要方向，加上后来兴起的人工生命研究，使得遗传算法受到了极大的关注。

遗传算法虽然具有良好的全局搜索能力，可以快速地搜索出解空间中的全体解，但算法存在收敛速度慢或易出现“早熟”现象等缺陷。文中针对遗传算法不足之处进行改进。为克服遗传算法中pc和pm不好确定的缺点，对pc和pm采用自适应过程。结合模拟退火算法的Metropolis准则，提高局部搜索能力，克服遗传算法早熟问题。同时为使遗传算法使用于k最短路问题，构造一种新的染色体编码方式和染色体的交叉操作。仿真结果表明，该算法可以提高运行效率，具有较高的精确度并且结构简明。

1 预备知识

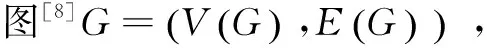
2 遗传算法和模拟退火算法

2.1 遗传算法基本步骤

遗传算法寻优过程其实是一个迭代的过程。把搜索的解空间映射为遗传的空间,将解映射成为染色体,向量中的每个元素称为基因,将所有的染色体组成种群,并按目标函数对每个染色体的优劣进行评价,并根据结果给出一个适应度值(fitness)。在这种情况下,每一代中各个体的特征可通过染色体遗传到一下代中。在下一代中,一个群体中合体相互之间可以复制(reproduction)和交叉(crossover),并会以一定的概率发生变异(mutation)。交叉倾向于选择群体中最为优秀的个体,这些交叉个体的最优特性相结合后产生的后代比父代具有更优良的特性,从而产生较好的解。遗传算法基本流程[9]如图1所示。

2.2 模拟退火基本原理与Metropolis准则

模拟退火算法(Simulated Annealing,SA)是模拟热力学中经典粒子系统的降温过程来求解规划问题的极值。当孤立粒子系统的温度以足够慢的速度下降时,系统近似处于热力学平衡状态,最后系统将达到本身的最低能量状态,即基态,这相当于能量函数的全局极小点。

模拟退火算法的基本原理如下：

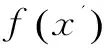
(3)若Δf≤0，则接受新点，作为下一次模拟的初始点。

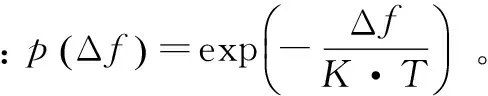
以上步骤称为Metropolis准则[10]。按照一定的退火方案逐渐降低温度,重复Metropolis过程,就构成了模拟退火优化算法。

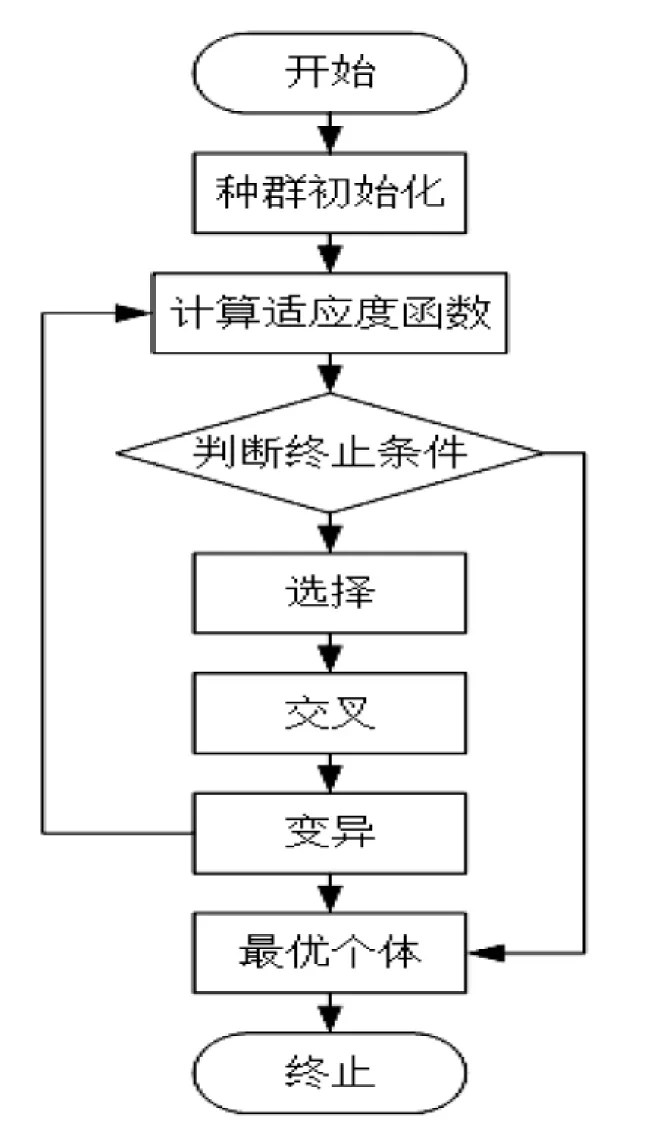
图1 遗传算法流程图

3 算法改进

3.1 染色体编码

结合k最短路径问题实际情况，文中定义了一种新的染色体编码方式。

假设在无向赋权图G=(V，E)中，初始节点Vs到目的节点Vt的路径为： 1→5→9→13→17→20。其中，每个数字代表的是节点编号，在遗传算法中可以作为每个染色体的基因，不同的路径包含有不同的基因点，所以设计染色体的编码方式为根据节点编号编码，上述路径的染色体编码为：[1-5-9-13-17-20]。

3.2 适应度函数和选择概率

(1)

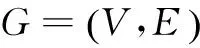
选择概率与其适应度呈比例，假设群体大小为N，第i个染色体的适应度为fi，第i个染色体被选中的概率为Pi，那么

(2)

显然个体适应度越大被选择的概率越高。

3.3 交叉操作与变异操作

交叉操作为两个父代个体的部分结构替换重组从而生成新个体的操作。文中采用两点交叉的方式，根据k最短路径问题定义一种新的交叉方式，如下所示：

父代1：

父代2：

子代1：

子代2：

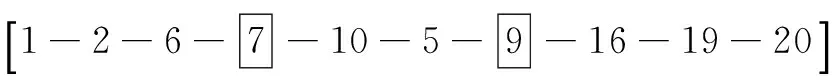
变异操作的基本内容是对群体中的染色体个体上的某些基因点的基因值进行变更。其目的是可以使遗传算法具备局部随机搜索能力和保持群体的多样性，避免出现未成熟就收敛的情况。在最短路问题中，选择要变异的路径，假设为Y：

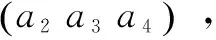
若变异后产生环路，按照交叉操作中所述进行处理。

3.4 交叉率(pc)与变异率(pm)的确定

遗传算法在进化过程中，进化程度与交叉率和变异率[11]的取值有很大关系，pc取值越大,新个体产生的速度越快，但当pc过大时又会使高适应度的个体结构快速被破坏，当pc取值过小时会使搜索过程缓慢,甚至停滞不前。当变异概率pm取值过小时,不易产生新的结构;当pm取值过大时,遗传算法就会变成纯粹的随机搜索算法。

所以文中采取自适应的遗传算法。根据交叉率和变异率对遗传算法群体进化过程中的影响，设计如下公式进行自适应调整：

pc1=0.9,pc2=0.2

(3)

pm1=0.01,pm2=0.05

(4)

其中，pc为两个交叉父代个体中适应度值较大的个体；favg为每一代群体的平均适应度值；fmax为群体中适应度值最大的个体。

当个体的适应度值小于平均值时，采用较高的pc和pm，使个体进化成为优秀个体的概率增大；当个体的适应度值大于平均适应度值时，采用较低的pc和pm，这样可以确保优秀个体的结构不容易被改变。

3.5 对最优个体进行模拟退火操作

模拟退火算法[12]的优点之一就是能以一定的概率接收较差解.也就是说算法即使陷入局部最优,理论上经过足够长的时间也可跳出来，从而收敛到全局最优解。新解是否被接受,判断的依据为Metropolis准则：

(5)

经过交叉操作后，若子代个体适应度变优,完全接收新解为当前解；若子代个体恶化,则以概率p接受恶化解为新的当前解。同时为了使每一代中优良个体结构不被破坏,采用精英保留策略[13],如果下一代群体中的最优个体适应度值小于当前群体最优个体适应度值,那么用当前群体中最优个体或者适应度值大于下一代最优个体适应度值的多个个体随机替代下一代群体中适应度差的相应数量的个体，确保了当前的最优个体不会因为交叉、变异等操作而被破坏。

3.6 算法流程

Step1:群体初始化，随机选取n条路径构成群体；

Step2:对群体中的每一个个体，根据式(1)和式(2)分别计算适应度值和选择概率；

Step3:按照Step2中得到的选择概率选择需要交叉操作的个体；

Step4:根据式(3)确定交叉率，根据3.3中所述的交叉方式进行交叉操作；

Step5:根据式(4)确定变异率，根据3.3中所述的变异方式进行变异操作；

Step6:按照模拟退火Metropolis准则对交叉后的个体是否接收进行操作；

Step7:根据精英保留策略对子代群体进行操作；

Step8:判断是否达到终止条件，若达到终止条件则输出前k个优秀解，否则转Step2。

4 仿真实验

仿真实验环境：处理器为Intel COREi5，操作系统为Windows7,应用MATLAB[14]编写。以图2为算例，其中共有30个网络节点，对算法的可行性及精确度进行实验。

图2 网络拓扑图

当k=10时，标准遗传算法(GA)与改进后遗传算法(GAM)所求v1到v30路径权值对比如图3所示。

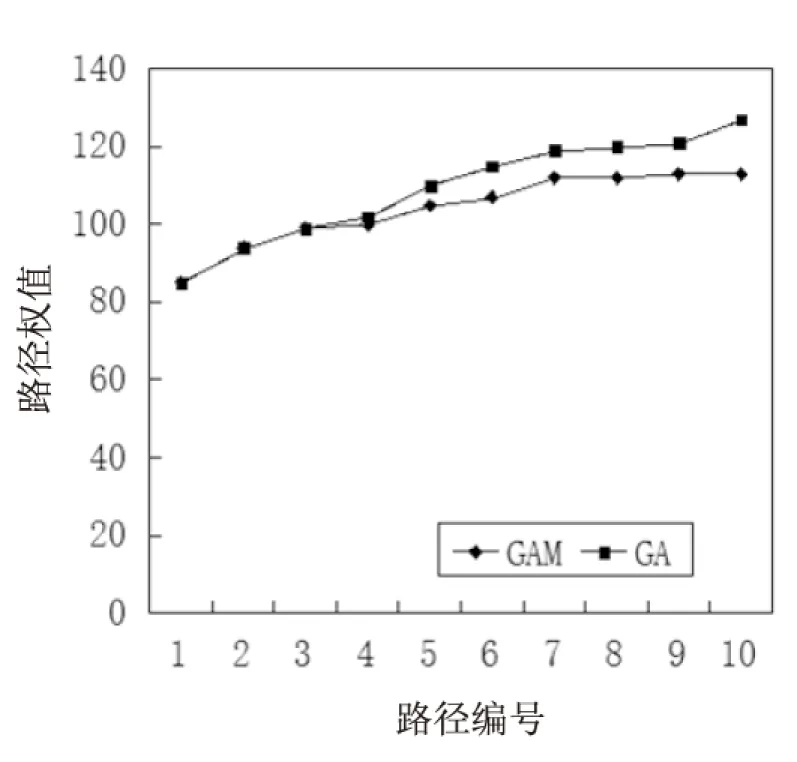
图3 求解结果精度对比

其中，初始种群个体数量n=100，迭代次数定为5 000，pc与pm由自适应公式得出，初始温度T0=200。

从图中可以看出，改进后的算法具有更高的精确度。

图4为两种算法在不同规模网络中求解时间的比较。起始求解网络规模为20个节点，150条边，每次求得结果后，网络拓扑图的节点个数和边的条数以5,50的数量递增，直到增加到50个节点、450条边为止。

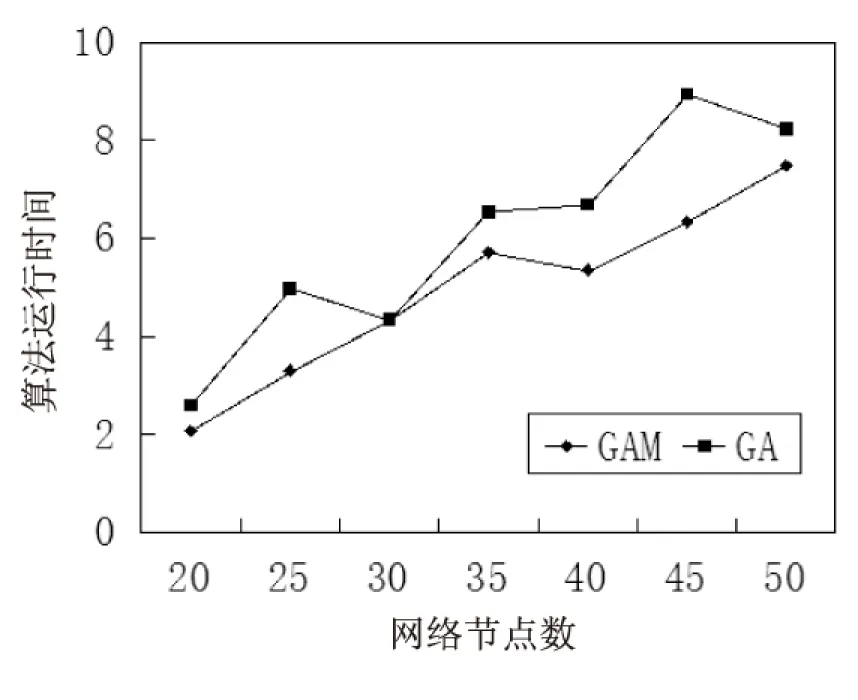
图4 两种算法求解时间对比

从图中可以看出，GAM平均时间效率高于GA，同时曲线更加平缓，说明稳定性也高于GA。

5 结束语

通过把遗传算法与模拟退火算法相结合，文中提出了一种求解k最短路径问题的新算法。通过对交叉率与变异率采用自适应的方式，构造了新的染色体编码方式及适应度函数，实现了对k最短路问题的求解。仿真结果表明，该算法能够较快较准确地找到多条最短路径，具有较高稳定性的同时克服了遗传算法易早熟的缺点。对求解一般复杂网络中k最短路问题，具有广泛的应用价值。

[1]PalmgrenM,YuanD.AshortsummaryonKshortestpath:algorithmsandapplications[EB/OL].1999.http://www.esc.auckland.ac.nz/Mason/Courses/LinkopingColCen99/kth.pdf.

[2]HoffmanW，PavleyR．AmethodofsolutionoftheNthbestpathproblem[J]．JournaloftheACM，1959，6(4):506-514．

[3] 柴登峰,张登荣.前N条最短路径问题的算法及应用[J].浙江大学学报:工学版,2002,36(5):531-534.

[4] 袁红涛,朱美正.K优路径的一种求解算法与实现[J].计算机工程与应用,2004,40(6):51-53.

[5]KangT，ZhangX，WangZ，etal．Algorithmforshortestpathofmulti-objectivesbasedonkshortpathalgorithm[J]．JournalofChangzhouInstituteofTechnology，2011，24(3):25-28．

[6]WangZ，HanW，LiY．Shortestpathproblemwithmultipleshortestpaths[J]．JournalofHarbinInstituteofTechnology，2010，42(9):1428-1431．

[7] 周 明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,2001.

[8] 谢 政,李建平.网络算法与复杂性理论[M].长沙：国防科技大学出版社，2003.

[9]AlsultannyYA,AqelMM.Patternrecognitionusingmultilayerneural-geneticalgorithm[J].Neurocomputing,2003,51:237-247.

[10] 康立山.非数值并行算法(第一册)：模拟退火算法[M].北京:科学出版社,2000:22-38.

[11] 赵礼峰，王小龙.图的Steiner最小树问题的混合遗传算法[J].计算机技术与发展,2014,24(10):110-114.

[12] 鲁建业,李 琦,董蕴华,等.采用混合遗传-模拟退火算法对DOE的直接设计[J].光电子·激光,2001,12(4):365-367.

[13]GaoErbao,LaiM.Animprovedgeneticalgorithmforthevehicleroutingproblemwithsimultaneousdeliveryandpickup[C]//Procofthe6thWuhaninternationalconferenceone-business-innovationmanagementtrack.Wuhan:[s.n.],2007:2100-2106.

[14] 王海英.MATLAB遗传算法工具箱及应用[M].北京:北京航空航天大学出版社,2010.

A Hybrid Genetic Algorithm for SolvingkShortest Path Problem

ZHAO Li-feng,YU Wen-yu

(College of Sciences,Nanjing University of Posts and Telecommunications,Nanjing 210023,China)

The key for the genetic algorithm is coding and the need to construct the fitness function.Combined with actualkshortestpathproblem,anewchromosomecodingmethodisredefinedandanewfitnessfunctionisconstructed.Thestandardgeneticalgorithmadoptsfixedcrossoverrateandmutationrate,andexiststhedefectsoflowconvergence,prematurityandpoorstability.Therefore,animprovedadaptivegeneticalgorithmisproposed,usingtheadaptivewayforthecrossoverrateandmutationrate,theformulafordeterminingthemisconstructtoacceleratetheconvergencespeed.Atthesametime,combinedwiththeMetropolisprincipleofsimulatedannealingtochoosethereceiveroftheoffspring,thealgorithmovercomestheproblemofpremature.Thesimulationshowsthattheimprovedhybridgeneticalgorithmcansolvethekshortestpathproblem,anditissuperiortothestandardgeneticalgorithminoptimizationaccuracy,timeefficiencyandstability.

hybrid genetic algorithm;chromosome code;Metropolis principle;kshortestpath

2015-10-25

2016-03-03

时间：2016-09-18

国家自然科学基金资助项目(61070234,61071167)

赵礼峰(1959-)，男，教授，硕士研究生导师，研究方向为图论及其在通信中的应用；于汶雨(1989-)，女，硕士研究生，研究方向为图论及其在通信中的应用。

http://www.cnki.net/kcms/detail/61.1450.TP.20160918.1707.020.html

TP

A

1673-629X(2016)10-0032-04

10.3969/j.issn.1673-629X.2016.10.007