基于局部回归和自相似性的图像超分辨率重建

李 欣，崔子冠，陈 杰，朱秀昌

(南京邮电大学 通信与信息工程学院，江苏 南京 210003)

基于局部回归和自相似性的图像超分辨率重建

李 欣，崔子冠，陈 杰，朱秀昌

(南京邮电大学 通信与信息工程学院，江苏 南京 210003)

近年来，基于样本的图像超分辨率重建逐渐成为研究热点，该算法一般利用外部训练样本，测试图像与训练样本的相似度在一定程度上影响着重建结果。针对此类问题，提出一种基于局部回归和自相似性的图像超分辨率重建算法。应用不同尺度图像间的自相似特性，对图像块建立一阶回归模型完成重建的算法，充分利用图像自身信息，并用稀疏表示的方法替代遍历搜索自相似块的方法，可以在自相似块不足的情况下保证重建质量。实验结果表明，该算法的重建质量较高，可以一定程度减少外部训练样本带来的虚假高频问题，且在重建质量与重建时间上有着较好的折中。

超分辨率；自相似性；局部回归；字典学习；稀疏表示

0 引 言

图像超分辨率(Super Resolution，SR)重建技术旨在从一个或多个低分辨率(Low Resolution，LR)输入图像中建立高分辨率(High Resolution，HR)图像，文中侧重于单幅图像超分辨率重建，即输入仅有一幅低分辨率图像。由于在从高分辨率到低分辨率的降质过程中有大量信息丢失，这是一个典型的病态问题，为了得到准确的唯一解，超分辨率重建需要辅助一些统计或结构先验[1-3]。

传统的多帧图像超分辨率重建如果得到的低分辨率图像具有亚像素平移(Subpixel Shifts)，重建时，一个高分辨率图像块就可以由多个相似又不完全相同的图像块组合而成。单图像超分辨率重建时，由于不具有这样的条件，常常利用机器学习的方法，借助外部图像训练集，找到高、低图像块间的联系，估计出图像块的高频信息[4-6]。一些研究[2,7-8]指出，当输入的LR图像与训练图像不匹配时，可能产生错误的高频信息。同时，一些研究[9-12]发现，自然图像中包含重复的视觉内容，即局部图像块会多次重复出现在跨尺度图像的不同位置，这种局部图像尺度不变性称为自然图像的自相似性(self-similarity)，这些自相似的图像块，可以看成是多帧图像超分辨率重建时那些具有亚像素平移的图像块，对这些图像块进行组合可以完成超分辨率重建。

在之前的研究中，笔者利用图像对应位(in-place)相似性[13]建立了一种局部回归模型，文中在此基础上提出一种基于局部回归和自相似性的单图像超分辨率重建方法，采用小尺度放大保证准确提取相似块的准确性，并采用PCA完成字典训练，保证算法的实用性。

1 基于局部回归和自相似性的图像超分辨率重建

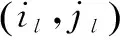
1.1 基于尺度不变性的对应位样本匹配

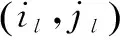
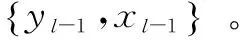
1.2 基于非局部自相似的加权一阶回归模型

(1)

xl≈u+

(2)

由式(2)可见，在局部一阶回归模型中无需直接得到映射函数，而只需要其梯度函数f。文中用主成分分析(PrincipalComponentAnalysis，PCA)对高分辨率及其低频带图像块对进行学习得到过完备字典，用稀疏表示的方法快速准确地估计出映射梯度函数f。

xl≈xl-1+

(3)

根据上述讨论，每次放大的尺度因子不能太大，通常s<2，且不为整数，这样下采样和上采样过程中存在亚像素采样或插值。正因为此，本中算法可以将多帧图像超分辨率重建时利用亚像素平移特性的优点结合到单图像超分辨率重建中，但这也造成对应位样本很难准确定位。考虑到自然图像具有丰富的非局部冗余特性，即空间位置并不直接相邻的一些图像块也可能具有非常相似的显著结构，文中算法为yl找到多个非局部自相似块的对应位样本对，对多个对应位样本块对分别重建的结果再加权平均。

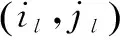
(4)

其中，权值wj满足：

(5)

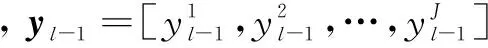
用最小二乘估计有：

(6)

由此，可以得到基于非局部自相似的加权一阶回归模型重建出的高分辨率图像块xl。

第l次放大的重建方案如图1所示。

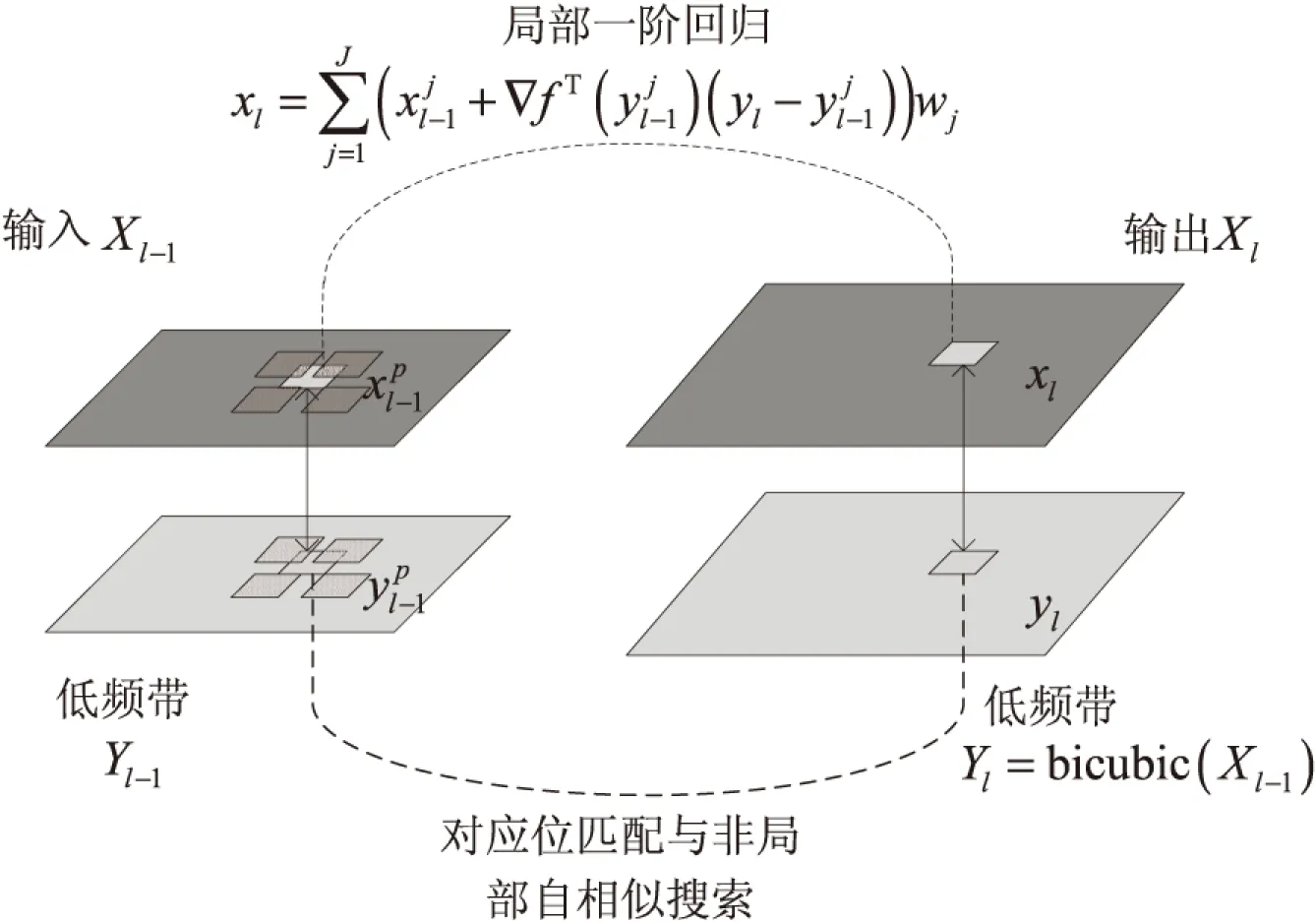
图1 第l次放大的重建方案示意图

1.3 字典学习

1.3.1 稀疏表示

Yang等[5-6]提出的基于稀疏表示的单图像超分辨率方法，由高分辨率自然图像建立一个过完备字典Φh∈RM×K，其中K列表示K个大小为M的“原子”，待重建的HR图像X中的任意块x∈RM可以由Φh的原子的稀疏线性组合表示。

x≈Φhα,‖α‖0≪K,α∈RK

(7)

观察到的LR图像中的块y可以用相同的稀疏表示系数向量α在相应的LR字典Φl上的线性组合表示，这可以由联合训练HR块和相应的LR块得到字典Φh和Φl来保证。

对于给定的输入LR图像块y，可以由下式求出稀疏解向量。

(8)

其中，F是一个特征提取算子。

将稀疏表示思想套入到文中算法，则低频带图像块yl-1对应式(8)中的LR图像块，式(8)改写为：

(9)

结合上文分析，选择一阶梯度为图像特征，故F是由一阶梯度滤波器组组成，包括：

(10)

F是将上述滤波器组应用到图像上得到的响应组合。结合文中算法及稀疏表示思想，式(7)改写为：

(11)

根据文中算法的思想，用于训练字典的样本是直接从输入图像或其上采样图像及其对应的低频带图像中采集的对应位样本图像块对，因而式(11)的稀疏表示实际上也就是用图像不同尺度上的自相似块来表征待重建图像块(特征)。

1.3.2 字典训练

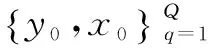
(12)

其中，Λk表示Pk在Φk上的稀疏表示系数矩阵；参数λ表示平衡系数的稀疏性及其对原始信号的逼近能力。

2 实 验

通过下列实验来验证文中算法的有效性。实验中参数设置：图像块大小5×5，放大倍数为3，尺度因子s=1.25；输入图像的低频带图像通过一个标准差为0.4的低通滤波器获得；非局部自相似块的个数J=10；字典学习阶段，每次随机选取的对应位样本图像块对个数固定为Q=10 000，分类数设为K=50。

将文中算法与Yang[5]提出的基于稀疏表示的超分辨重建算法、Freedman[8]提出的基于局部自相似样本的图像超分辨重建算法、Glasner[7]提出的基于图像块尺度不变的图像超分辨率重建算法进行比较，如表1所示。

表1 各超分辨率重建方法PSNR对比(×3)

表1给出了文中算法与相关算法超分辨率图像重建的PSNR值。实验结果显示，文中算法取得了最好的重建质量。Yang的基于稀疏表示的超分辨率重建算法前面章节已有讨论，重建图像的质量较好，对于一些自相似性不是非常明显的图像(如Koala、Girl、Zebra)，其重建结果甚至高于Freedman的算法；Freedman的算法属于快速算法，对于重建模型中的部分先验是根据经验设计的，故该算法的图像重建质量一般要低于Glasner和文中算法；与文中算法重建质量最为接近的是Glasner算法，该算法通过对输入的低尺度图像再次下采样，从低尺度图像及多层下采样图像中找到足够多的自相似块来完成重建，对于少数图像的重建效果与文中算法相当或略高。

图2、图3分别是测试图像放大3倍的结果，其主观效果与表1的客观参数结果相当，而且文中算法的主观重建质量也是最优的。Koala属于毛发细节丰富的图像，除了双立方插值，其余四种算法都是基于图像块处理的，对重叠图像块分别重建平均，所以最终重建出来的图像中毛发都无法如原始图像那样细，会显得比较模糊，相比较而言，文中算法对于耳朵部分毛发的重建效果与原始高分辨率图像最相近。Parthenon属于内部图像块自相似性较强的图像，因而基于图像块自相似的算法重建质量要优于基于稀疏表示的算法，Freedman算法出现了一些错误的重建细节，Glasner和文中算法重建结果比Freedman的错误细节要少得多，文中算法与原始高分辨率图像相比细节重建的准确度更高。

图2 各种算法对Koala图像的超分辨率重建结果

图3 各种算法对Parthenon图像的超分辨率重建结果

对于运行时间，Freedman的算法为了减少运算量，未对整幅图像的所有自相似块进行搜索，而是根据经验设计出重建模型中的滤波器或映射函数，估计重建速度较快，一般一幅256×256图像三倍放大的重建时间约在几秒内就可完成；Glasner算法重建除了多层迭代放大，还要多输入图像向下采样得到更低尺度图像来搜索足够多的自相似块，运算时间约在5～6min；文中算法利用分类字典稀疏表示，不需要逐个搜索自相似块，但每次迭代放大时都需要进行字典训练，故实验中选择了图像块分类+PCA训练的处理缩短了运算时间，一般每次需要20s左右，对于三倍放大需要约2～3min。

3 结束语

局部图像块会多次重复出现在相同的尺度图像和不同的尺度图像中这种图像块的尺度不变性，为超分辨率重建提供了很好的方向。利用图像自身图像块的自相似性进行图像重建，可以不借助外部训练图像样本，完成图像超分辨率重建。文中提出一种利用图像的自相似性对图像块建立一阶回归模型完成重建的算法。实验结果表明，该算法的重建质量较高，可以一定程度减少外部训练样本带来的虚假高频问题，而且在重建质量与重建时间上都有较好的折中。

[1]DaiS,HanM,XuW,etal.Softcuts:asoftedgesmoothnesspriorforcolorimagesuper-resolution[J].IEEETransactionsonImageProcessing,2009,18(5):969-981.

[2]FattalR.Imageupsamplingviaimposededgestatistics[J].ACMTransactionsonGraphics,2007,26(3):95-102.

[3]SunJ,XuZ,ShumHY.Gradientprofileprioranditsapplicationsinimagesuper-resolutionandenhancement[J].IEEETransactionsonImageProcessing,2011,20(6):1529-1542.

[4]WangQ,TangX,ShumH.Patchbasedblindimagesuperresolution[C]//ProcoftenthIEEEinternationalconferenceoncomputervision.[s.l.]:IEEE,2005:709-716.

[5]YangJ,WrightJ,HuangTS,etal.Imagesuper-resolutionviasparserepresentation[J].IEEETransactionsonImageProcessing,2010,19(11):2861-2873.

[6]YangJ,WangZ,LinZ,etal.Coupleddictionarytrainingforimagesuper-resolution[J].IEEETransactionsonImageProcessing,2012,21(8):3467-3478.

[7]GlasnerD,BagonS,IraniM.Super-resolutionfromasingleimage[C]//Procof12thinternationalconferenceoncomputervision.[s.l.]:[s.n.],2009:349-356.

[8]FreedmanG,FattalR.Imageandvideoupscalingfromlocalself-examples[J].ACMTransactionsonGraphics,2011,30(2):474-484.

[9]YangCY,HuangJB,YangMH.Exploitingself-similaritiesforsingleframesuper-resolution[C]//ProcofACCV.Berlin:Springer,2010:497-510.

[10]YangJ,LinZ,CohenS.Fastimagesuper-resolutionbasedonin-placeexampleregression[C]//ProcofIEEEconferenceoncomputervisionandpatternrecognition.[s.l.]:IEEE,2013:1059-1066.

[11]HuJ.Single-imagesuperresolutionbasedonlocalregressionandnonlocalself-similarity[J].JournalofElectronicImaging,2014,23(3):6-8.

[12]PanL,YanW,ZhengH.Super-resolutionfromasingleimagebasedonlocalself-similarity[J].MultimediaToolsandApplications,2015,25(8):1-21.

[13] 李 欣，崔子冠，孙林慧，等.基于局部回归模型的图像超分辨率重建[J].计算机应用，2016，36(6)：1654-1658.

[14]GuoC,ZhuSC,WuYN.Primalsketch:integratingstructureandtexture[J].ComputerVisionandImageUnderstanding,2007,106(1):5-19.

Image Super-resolution Reconstruction Based on Local Regression and Self-similarity

LI Xin,CUI Zi-guan,CHEN Jie,ZHU Xiu-chang

(College of Telecommunications & Information Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)

In recent years,image super-resolution reconstruction based on samples has gradually become a hot research topic,which usually uses the external training samples.The similarity between the test image and the training samples affects the reconstruction results to a certain extent.To solve this problem,a super-resolution image reconstruction algorithm based on local regression and self-similarity is proposed.This algorithm,which makes use of the self-similarity between images at different scales and reconstructs the image by establishing the first-order autoregressive model of the patches,could make full use of the information of the image itself,and replace the traversal search of self-similar patches with the sparse representation method.So it can guarantee the reconstruction quality even the number of the self-similar patches is not enough.The experimental results show that the reconstruction quality of this algorithm is high.It can alleviate the false high-frequency problem brought by the external training samples to a certain extent and have a good tradeoff between the reconstruction quality and reconstruction time.

super-resolution;self-similarity;local regression;dictionary learning;sparse representation

2015-12-28

2016-04-21

时间：2016-09-19

国家自然科学基金青年基金项目(61501260)；江苏省自然科学基金项目(BK20130867,BK20140891)；江苏省高校自然科学基金项目(13KJB510020)；江苏省普通高校研究生科研创新计划(CXLX12_0474)

李 欣(1981-)，女，讲师，博士研究生，研究方向为图像超分辨率重建、多媒体通信；朱秀昌，教授，博士生导师，研究方向为多媒体信息，图像和视频的采集、处理、传输和显示。

http://www.cnki.net/kcms/detail/61.1450.TP.20160919.0841.024.html

TP301.6

A

1673-629X(2016)10-0017-05

10.3969/j.issn.1673-629X.2016.10.004