一种基于身份的广义签密方案
2016-02-27祁正华杨红尘
祁正华,杨红尘,黄 海
(南京邮电大学 计算机学院、软件学院,江苏 南京 210003)
一种基于身份的广义签密方案
祁正华,杨红尘,黄 海
(南京邮电大学 计算机学院、软件学院,江苏 南京 210003)
为了解决安全性需求不确定网络环境的安全性问题,广义签密方案被提出,其具有灵活多变的特点,能在一个密码模块内实现签密、加密和签名三种功能。以提高计算效率和实现更高的安全性为目标,研究分析了以往高效安全的广义签密方案,给出了一种新的基于身份广义签密方案。从各方面对该方案进行了安全性的证明与分析,并将该方案与目前计算效率较高的广义签密方案进行了比较,还给出了一个该方案的应用实例,描述了该方案在邮件系统中的具体运用过程。结果表明,新方案的椭圆曲线点乘运算、双线性对运算的次数都有所降低。
广义签密;基于身份密码体制;双线性对;签密
1 概 述
根据加密算法和解密算法所用到的密钥的不同情况,可将加密算法分为对称加密和非对称加密(又被称为私钥加密和公钥加密)。私钥加密中加密算法与解密算法所使用的密钥是相同的,或者是两个密钥之间的推导比较简单,即无论是加密密钥还是解密密钥泄露都会影响整个算法的安全性;公钥密码虽然具有许多优点,但是公钥密码的公钥认证和证书管理相当复杂,且成本昂贵,其基本思想是让加密算法和解密算法使用不同的密钥,加密密钥公开私钥保密,且很难从用户的公钥推导出用户的私钥,这样只要未授权者没有合法用户的私钥信息就无法轻易地获得明文。1984年,Shamir[1]为了简化证书管理,建设性地提出了基于身份的公钥密码系统的思想,其公钥直接为实体的身份信息,因此基于身份的公钥密码体制可以很自然地解决公钥与实体的绑定问题。2001年,Boneh D等[2]在椭圆曲线双线性对的基础上提出了第一个基于身份的加密方案,但该方案在随机预言机模型下才能证明其安全性。2002年,Malone-Lee[3]最先提出了完整的基于身份的签密方案,但Libert等[4]指出该方案并不满足语义安全性。此后,许多不同的签密算法相继提出[5-7]。
在现实中存在一些网络环境,其安全性要求并非是确定的,系统中并不是只要存有签名、加密或者签密方案其中之一就能满足所有网络事务的需求,这样一些网络系统中就必须同时存有这三种方案,且系统要根据不同的安全性要求使用不同的方案,这种做法由于增加了算法存储空间和方案之间的切换机制,故明显增加了系统负担。广义签密的提出解决了上述不足,其不仅具有普通签密方案的特性,还可以只实现机密性或认证性一种功能,在时间和成本上能够满足不同需求的网络环境。适用于用户之间需要频繁传输不同秘密级别消息的网络环境。
广义签密(Generalized SignCryption,GSC)是韩益亮等[8-9]提出的密码学概念。其将签名、加密、签密三种算法实现的功能集于一身,且将这三种方案作为可供选择的不同模式根据输入情况判断具体实现中所用到的是哪一种功能。广义签密的出现解决了那些安全性需求不稳定的网络环境需要存储多种密码方案且需要来回转换不同方案的存储空间和时间的高消耗问题。2007年,Wang X等[10]定义了GSC体制的安全模型。鉴于GSC方案的灵活多变性,许多学者将其与基于身份签密相结合,形成了基于身份GSC方案。2008年,Lai S等[11]提出了基于身份GSC体制的形式化定义和安全模型,并提出了一种具体方案。此后,一些优秀的基于身份GSC方案相继提出[12-14],其都从计算效率或安全性方面对前人提出的方案进行了改进。
文中提出了一种新的基于身份GSC算法,验证了算法的正确性并分析了其安全性和性能。
2 相关基础
2.1 双线性对
设G1,G2分别是阶数为q(大素数)的加法群和乘法群。P为G1的一个生成元,称e:G1×G1→G2是一个双线性映射,当其满足以下性质时。
(1)双线性。对所有的P,Q,R∈G1,都有:
e(aP,bQ)=e(P,Q)ab
e(P+Q,R)=e(P,R)e(Q,R)
e(P,Q+R)=e(P,Q)e(P,R)
(2)非退化性。存在P,Q∈G1,满足e(P,Q)≠1,如果e(P,Q)=1,那么说明点P为无穷远的点。
(3)可计算性。对所有的P,Q∈G1能够找到可行的算法计算e(P,Q)的值,那么称e为双线性配对。
2.2 困难问题假设
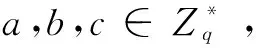
2.3 基于身份广义签密算法定义
基于身份GSC算法由以下四个算法组成:
1)系统生成(Setup):系统选择一个安全参数k,PKG经过选择和计算得出系统公开的初始化参数列表params和系统的主密钥s。
2)用户私钥生成(Extract):根据用户的身份IDA,PKG利用系统的公开参数和主密钥s计算出该身份信息对应的私钥SA,并通过一个安全信道传送给用户。
3)广义签密(GSC):该算法有三种不同的工作方式,即签密、加密和签名,每次只有其中一个工作方式发生。
(1)签密:若用户IDA需要让传输的消息m同时满足机密性和可认证性之后再发送给接收者B,发送者A已知的信息有(SA,m,IDB),利用已知的信息执行GSC算法生成密文为σ=GSC(SA,m,IDB)。
(2)签名:若用户IDA仅需要签名一个消息m而不用特别指定签名的接收者时,这时接收者的身份信息是没有的。发送者A已知的信息有(SA,m,ID∅)。其中,ID∅表示身份为空的情形。用户A执行GSC算法生成密文σ=GSC(SA,m,ID∅),这种情况下的GSC算法发挥的作用就相当于一个签名算法。
(3)加密:若某用户仅仅是需要传输的信息m满足数据的机密性而对数据的可认证性没有要求,即没有发送者的身份信息,只是加密一个消息,此时的已知信息是(S∅,m,IDB),其中S∅表示身份信息为空时的私钥。利用已知信息执行GSC算法生成σ=GSC(S∅,m,IDB),在这种情况下的GSC算法的作用就相当于一个加密算法。
4)解广义签密(UGSC):GSC算法无论工作在何种方式下,在进行解广义签密时都进行相同的操作。经过判断,若σ是一个有效密文,则接收者B运行解签密算法解密密文信息返回m,若广义签密运行的是签密或者签名功能的话还要返回A对消息m的签名信息;否则返回Г表示密文无效。
3 基于身份GSC方案

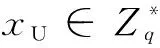
GSC:(用户A想要安全地发送消息m给B)首先计算f(IDA)、f(IDB)的值,若都为0,则无意义,终止。否则进行如下计算:
(2)计算R=kP,R1=xAPpub,S=k-1(f(IDA)SA+H2(R)P);
(3)计算w=e(Ppub,QB)k·f(IDB),C=H3(w)⊕(m‖S);
(4)发送密文σ=(C,R,R1,S)给B。
UGSC:接收者B接收到密文σ后,进行如下计算:
(1)计算w=e(R,DB)f(IDB);
(2)计算m‖S=H3(w)⊕C。
在接收到密文之后,首先要判断等式e(R,S)=e(R1,QA)f(IDA)·e(P,P)H2(R)是否成立,成立则B接收此密文消息,否则将此密文视为无效。
正确性验证:
e(R,S)=e(kP,k-1(f(IDA)SA+H2(R)P))=e(P,SA)f(IDA)·e(P,P)H2(R)=e(P,xAsQA)f(IDA)·e(P,P)H2(R)=e(xAsP,QA)f(IDA)·e(P,P)H2(R)=e(R1,QA)f(IDA)·e(P,P)H2(R)
4 安全性和计算量分析
4.1 安全性分析
下面从5个方面来分析新算法的安全性。
(1)机密性:假设存在一个接收者F能在多项式的时间t内解密消息。其中,F通过截取区域内的广播消息可以得到σ=(C,R,R1),已知R=kP,Ppub=sP,令QB=bP(F并不知道k,b,s)。如果F想解密消息的话,其必须能在多项式时间t内解出e(Ppub,QB)k=e(P,P)kbs的值。即F能在多项式时间t内根据R,QB和Ppub计算出e(Ppub,QRi)k,即其能够在多项式时间内解决DBDH问题。由于DBDH问题在多项式时间内是不可解的,这与假设的结论矛盾。因此,假设不成立,该算法具有机密性。
(2)不可伪造性:因为攻击者F无法获得发送者Alice的加密私钥SA和随机数xA,所以其不能正确计算出S=k-1(f(IDA)SA+H2(R)P)和R1=xAPpub,即不能伪造发送者的签密消息,因此该算法满足不可伪造性。
(3)公开验证性:由于验证密文是通过判断等式e(R,S)=e(R1,QA)f(IDA)·e(P,P)H2(R)是否成立,该等式中用到的信息都是可计算的或者是可以公开获得并不涉及发送者、接收者的私钥信息,因此该算法满足公开验证性。
(4)不可否认性:因为该方案满足公开验证性,所以也满足不可否认性。
(5)前向安全性:即便攻击者F获得了发送者Alice的私钥SA,但攻击者F并不知道随机数k和接收者Bob的私密钥DB,所以其无法求得e(Ppub,QB)k·f(IDB)或者e(R,DB)f(IDB),进而无法解出m,因此F无法解签密消息。所以,该算法具备前向安全性。
综上所述,该算法能够满足机密性、不可伪造性、公开验证性、不可否认性和前向安全性,是一种安全的基于身份广义签密方案。
4.2 计算量分析
计算开销和密文长度是影响算法效率的两个主要因素。影响算法计算效率的主要运算是椭圆曲线点乘运算、双线性对运算和指数运算,分别用字母M,P和E表示。表1给出了新方案与当前效率较高的其他广义签密方案的比较情况。

表1 基于身份广义签密方案的比较
5 新方案在电子邮件系统中的应用
利用文中提出的广义签密方案,设计一个安全的电子邮件传送机制,提供发送私人邮件、公告邮件的发送模式。该邮件发送机制的整体构架如图1所示。
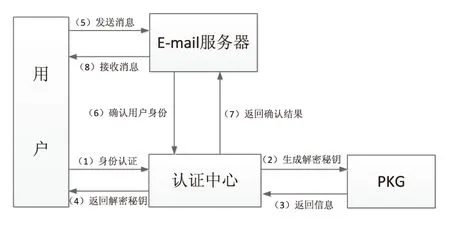
图1 邮件发送机制的整体构架
首先,用户计算自己的公钥,向认证中心提出身份认证请求,通过后认证中心向PKG申请用户的解密私钥,PKG根据用户的公钥信息,计算出用户的解密密钥并通过安全信道传送给用户,当用户获取该解密密钥之后,计算出其加密密钥。与E-mail服务器进行邮件传输,当E-mail服务器收到用户邮件传输请求后,要向认证中心确认用户身份信息,如果用户身份正确,则进行信息交换,否则,拒绝邮件发送请求。接收者接收到加密邮件后若不能正确解密邮件信息,则视为无效邮件,不做处理。
5.1 身份认证
用户的客户端根据电子邮件系统的要求,将自己的身份信息IDU和自己的公钥信息QU发送给认证中心,认证中心检测IDU是用户的真实身份信息且能保证使用的唯一性,则通过身份认证。
5.2 用户私钥对生成
当用户的身份信息通过认证后,认证中心将用户的公钥信息QU发送给PKG,PKG计算出用户的解密密钥DU,并通过安全的信道传送给用户U,用户U再根据该解密密钥计算出加密密钥SU,并将
5.3 邮件的发送和接收过程
邮件的发送过程为发送者Alice签密明文后,通过E-mail服务器将邮件发送给接收者Bob的过程,具体如下:判断f(IDB)。若等于0,则发送者发送的是公开邮件,等于1则为私人邮件。然后发送者Alice执行第3节GSC算法计算出密文σ=(C,R,R1),通过E-mail服务器发送给接收者Bob。当Bob接收到邮件后,判断w的值是否为0,为0则接收到的是公开邮件,否则是私人邮件。根据判断UGSC算法中正确性验证等式是否成立,判定接收到的密文是否有效,有效则Bob执行解密算法解密密文邮件,否则视为垃圾邮件不做处理。
6 结束语
文中提出了一种新的基于身份广义签密方案。从机密性、不可伪造性、公开验证性、不可否认性和前向安全性这五个方面进行了安全性分析,并将该方案与目前计算效率较高的广义签密方案进行了比较,结果表明该方案是一个安全高效的基于身份广义签密方案。同时给出了一个应用实例,讲述了将该算法应用于邮件系统的具体工作流程。
[1]ShamirA.Identity-basedcryptosystemsandsignatureschemes[C]//Proceedingsofadvancesincryptology-CRYPTO’1984.Berlin:Springer-Verlag,1985:47-53.
[2]BonehD,FrankklinM.IdentitybasedencryptionfromtheWeilPairing[C]//ProceedingofCrypto’01.Berlin:Springer-Verlag,2001:213-229.
[3]Malone-LeeJ.Identitybasedsigncryption[R/OL].2011-10-01.http://eprint.iacr.org/2002/098.pdf.
[4]LibertB,QuisquaterJJ.Newidentitybasedsigncryptionschemesfrompairings[EB/OL].2003-02-03.http://eprint.iacr.org.
[5]QiZhenghua,RenXunyi,YangGeng.Provablysecuregeneralaggregatesigncryptionschemeintherandomoraclemodel[J].ChinaCommunications,2012,9(11):107-116.
[6]RenXunyi,QiZhenghua,YangGeng.Provablysecureaggregatesigncryptionscheme[J].ETRIJournal,2012,34(3):421-428.
[7] 明 洋,冯 杰,胡齐俊.标准模型下安全基于身份代理签密方案[J].计算机应用,2014,34(10):2834-2839.
[8] 韩益亮,杨晓元.ECDSA可公开验证广义签密[J].计算机学报,2006,29(11):2003-2012.
[9]HanYiliang.Generalizationofsigncryptionforresources-constrainedenvironments[J].WirelessCommunicationandMobileComputing,2007,7(7):919-931.
[10]WangX,YangX,HanY.Provablesecuregeneralizedsigncryption[EB/OL].2007.http://eprint.iacr.org/2007/173.
[11]LaiS,KushwahP.ID-basedgeneralizedsigncryption[EB/OL].2008-02-26.http://eprint.iacr.org/2008/084.
[12] 张洪礼,赵 静,刘文远.高效的基于双线性对和身份的广义签密方案[J].计算机应用研究,2010,27(2):678-681.
[13] 项顺伯.可证安全的基于身份的广义签密方案[J].信息网络安全,2013(1):58-60.
[14] 周才学.无可信中心的基于身份的广义签密[J].计算机科学,2013,40(4):142-146.
An Identity-based Generalized Signcryption Scheme
QI Zheng-hua,YANG Hong-chen,HUANG Hai
(School of Computer Science and Technology,School of Software,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)
For meeting the requirements of security in unstable network environment,generalized signcryption is proposed.It has flexible features,and can achieve signcryption,encryption and signature within one cryptographic module.In order to improve the computational efficiency and security,analysis of the proposed schemes,a new identity-based generalized signcryption program is put forward.The security of this scheme is proved from all aspects,then it is in contrast with the proposed schemes which has high computational efficiency.An application example of the scheme is given and the process of applying the program is described in mail system.The results show that the new scheme reduces the numbers of computation of the pairing and scalar multiplication.
generalized signcryption;identity-based cryptography;bilinear pairing;signcryption
2015-09-10
2016-02-25
时间:2016-09-18
国家自然科学基金资助项目(61073188)
祁正华(1975-),女,副教授,博士,研究方向为网络与信息安全;杨红尘(1991-),女,硕士研究生,研究方向为网络与信息安全。
http://www.cnki.net/kcms/detail/61.1450.TP.20160918.1707.016.html
TP309
A
1673-629X(2016)10-0083-04
10.3969/j.issn.1673-629X.2016.10.018
