一类典型余模代数的等变分解

俞晓岚

(杭州师范大学理学院, 浙江 杭州 310036)



一类典型余模代数的等变分解

俞晓岚

(杭州师范大学理学院, 浙江 杭州 310036)

摘要：本文给出了非退化双线性型量子自同构群的一类典型余模代数的等变分解, 由此得知此类余模代数满足Hochschild同调和上同调间的Poincaré对偶.

关键词：典型余模代数;等变分解;Poincaré对偶

0引言

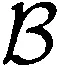
上述结论启发人们思考这样一个问题:如果两个Hopf代数H和L的余模范畴是等价的,那么它们的Hochschild上同调之间有什么关系?这个问题目前还没有解决,与之相关的一个问题是:如果两个Hopf代数H和L的余模范畴是等价的,那么如何从H的双模投射分解得到L的双模投射分解.Bichon在文献[5]中提出了余模代数的等变(equivariant)自由分解的概念.如果两个Hopf代数H和L的余模范畴是等价,并已知H的一个等变自由分解,那么就可以利用H的这个分解得到L的自由分解.但如何利用H和L的这两个分解来研究它们Hochschild同调间的关系,目前还没有找到有效的方法.因此,我们需要丰富的等变自由分解的例子来解决这一问题.

1准备知识

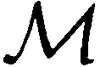
设M是A-双模,μ,ν是A的自同构,双模μMν作为向量空间和M是同构的,但左,右模结构分别定义为a·m·b=μ(a)mν(b),其中,a,b∈A,m∈M.下文中为简单起见,如果μ或者ν是恒等映射,就省略不写.

接下去,我们简单回顾两个基本概念.

定义1假设H是Hopf余半单代数.如果一个右H-余模代数A满足每个单H-余模是A的直和项,且重数恰好是1,就称A是一个典型H-余模代数(modelH-comodule algebra).

定义2假设H是Hopf代数,A是右H-余模代数.A的一个H-等变自由分解(H-equivariant free resolution)指的是一个正合列

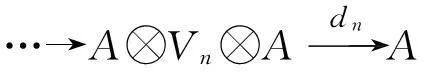
其中,对n≥1,Vn是右H-余模,dn既是A-双模态射,又是右H-余模态射.显然,A的一个H-等变自由分解首先是A的自由双模分解.

2主要结果

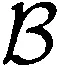
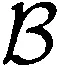
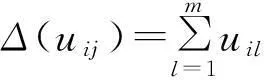
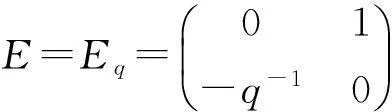
这里□表示余张量函子.

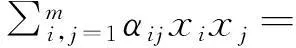
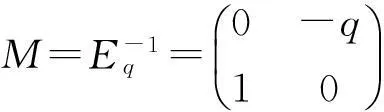
假设F∈GLn(k)满足tr(E-1Et)=tr(F-1Ft),m,n≥2,:→是由(E)-(F)-双Galois对象(E,F)诱导的等价函子,那么存在(F)-余模代数同构(E-1,t)≌F-1,t.

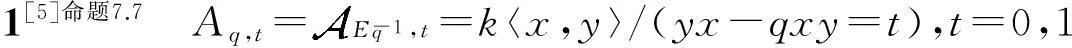
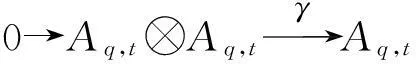
(1)

其中V=kx⊕ky,态射γ定义为γ(1⊗1)=-qx⊗y⊗1-q1⊗x⊗y+y⊗x⊗1+1⊗y⊗x.

引理4[5]命题7.6假设H,L是Hopf代数,且存在余模范畴的等价函子:H→L.设A是右H-余模代数,那么任意一个A的H-等变自由分解

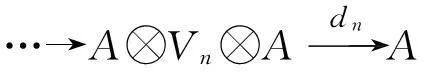
…→(A)⊗(Vn)⊗(A)→(A)⊗(Vn-1)⊗(A)→…

→(A)⊗(V2)⊗(A)→(A)⊗(V1)⊗(A)→(A)⊗(A)→(A)→0.

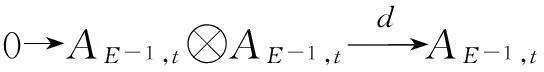
(2)

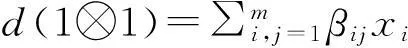
证由于存在q∈k*,使得tr(E-1Et)=-q-q-1,那么由引理1知,=-□(Eq,E):→是等价函子.由引理4及其在文献[5]中的证明知,对Aq,t的等变自由分解(1)作用函子,再利用同构(Aq,t⊗Aq,t)≌(Aq,t)⊗(Aq,t),(Aq,t⊗V⊗Aq,t)≌(Aq,t)⊗(V)⊗(Aq,t),就可得到E-1,t的等变自由分解.由引理2知,(Aq,t)≌E-1,t.同时,有余模同构

□

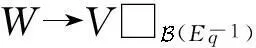
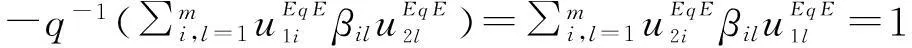
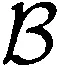
(i)是2维扭Calabi-Yau代数,Nakayama自同构μ定义为μ(x1,…,xm)=-(x1,…,xm)(E-1)tE.

(ii)满足Hochschild同调和上同调间的Poincaré对偶Hi(A,M)≌H2-i(A,μM),0≤i≤2,

其中M是A-双模.

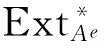
HomAe(A⊗A,Ae)→HomAe(A⊗W⊗A,Ae)→HomAe(A⊗A,Ae).

(3)

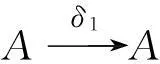
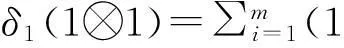
由分解式(2),可得正合列0→A⊗Aμ→A⊗W⊗Aμ→A⊗Aμ→Aμ→0,

其中μ即为定理中定义的A的自同构.又有复形同构:

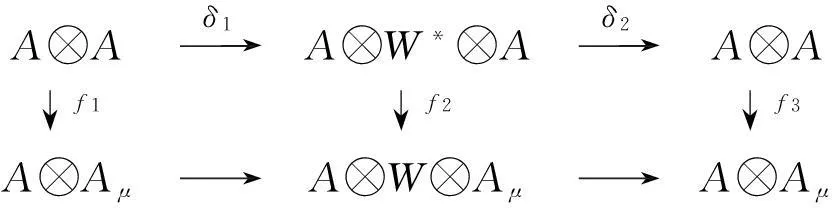
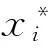
(ii)是(i)和[9，定理1]的直接推论.

参考文献:

[1] DUBOIS-VIOLETTE M, LAUNER G. The quantum group of a non-degenerate bilinear form[J]. Phys Lett B,1990,245(2):175-177.

[2] BICHON J. Hochschild homology of Hopf algebras and free Yetter-Drinfeld resolutions of the couint[J]. Compos Math, 2013,149(3):658-678.

[3] COLLINS B, HRTEL J, THOM A. Homology of free quantum groups[J]. Comptes Rendus Mathematique,2009,347(5):271-276.

[4] HADFIELD T, KRHMER S. Twisted homology of quantum SL(2)[J]. K-Theory, 2005,34(4):327-360.

[5] BICHON J. Hopf-Galois objects and cogroupoids[J]. Rev Un Mat Argentina, 2014,55:11-69.

[6] KLIMYK A, SCHMÜDGEN K. Quantum groups and their representations[M]. Berlin: Springer, 1997.

[7] DUBOIS-VIOLETTE M. Multilinear forms and graded algebras[J]. J Algebra, 2007,317(1):198-225.

[8] LIU L Y, WANG S Q, WU Q S. Twisted Calabi-Yau property of Ore extensions[J]. J Noncommut Geom, 2014,8:587-609.

[9] VAN DEN BERGH M. A relation between Hochschild homology and cohomology for Gorenstein rings[J]. Proc Amer Math Soc, 1998,126(5):1345-1348.

[10] HE J W, VAN OYSTAEYEN F, ZHANG Y H. Deformations of Koszul Artin-Schelter Gorenstein algebras[J]. Manuscripta Math, 2013,141(3-4):463-483.

第15卷第1期2016年1月杭州师范大学学报(自然科学版)JournalofHangzhouNormalUniversity(NaturalScienceEdition)Vol.15No.1Jan.2016

Equivariant Resolutions for a Class of Model Comodule Algebras

YU Xiaolan

(School of Science, Hangzhou Normal University, Hangzhou 310036, China)

Abstract:This paper gives equivariant resolutions for a class of model comodule algebras of quantum automorphism groups of non-degenerate bilinear forms. Consequently,such comodule algebras satisfies the Poincaré duality between Hochschild homology and cohomology.

Key words:model comodule algebra; equivariant resolution; Poincaré duality

文章编号:1674-232X(2016)01-0067-04

中图分类号:O154MSC2010: 16E05;16W35;16E40

文献标志码:A

doi:10.3969/j.issn.1674-232X.2016.01.013

通信作者：俞晓岚(1982—),女,副教授,博士,主要从事非交换代数的研究.E-mail:xlyu@hznu.edu.cn.

基金项目：国家自然科学基金项目(11301126)；浙江省自然科学基金项目(LQ12A01028).

收稿日期：2015-08-27